Toán lớp 4 trang 69 - Bài 59: Luyện tập chung - SGK Kết nối tri thức

Câu 1

a) Số?

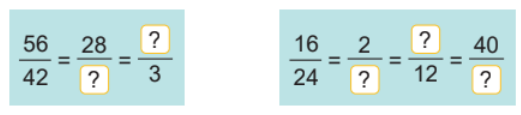
b) Rút gọn các phân số: \(\frac{{40}}{{25}};\,\,\frac{{63}}{{81}};\;\,\,\frac{{36}}{{60}}\)

Phương pháp giải:

a) Áp dụng tính chất cơ bản của phân số:

- Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.

- Nếu chia hết cả tử và mẫu số của một phân số cho cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho. 

b) Cách rút gọn phân số:

- Xét xem tử số và mẫu số cùng chia hết cho số tự nhiên nào lớn hơn 1.

- Chia tử số và mẫu số cho số đó.

Cứ làm như thế cho đến khi nhận được phân số tối giản

Lời giải chi tiết:

a)

b) \(\frac{{40}}{{25}} = \frac{{40:5}}{{25:5}} = \frac{8}{5}\)

\(\frac{{63}}{{81}} = \frac{{63:9}}{{81:9}} = \frac{7}{8}\)

\(\;\frac{{36}}{{60}} = \frac{{36:12}}{{60:12}} = \frac{3}{5}\)

Câu 2

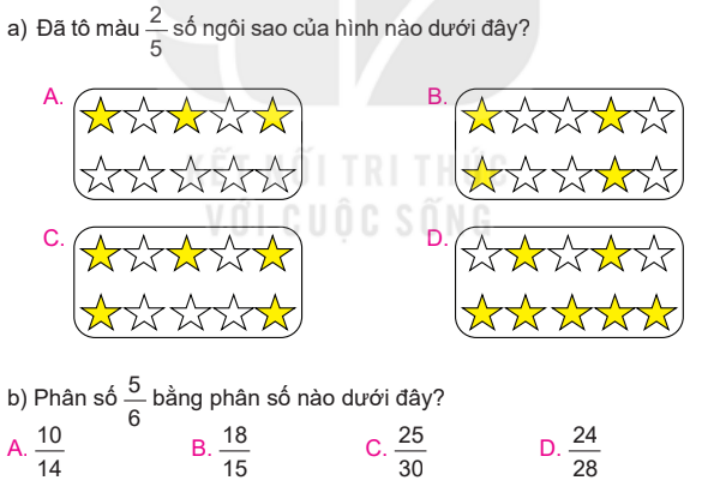
Chọn câu trả lời đúng.

Phương pháp giải:

a) Phân số chỉ số phần được tô màu có tử số là số phần được tô màu và mẫu số là số phần bằng nhau.

b) Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác 0 thì được một phân số bằng phân số đã cho.

Lời giải chi tiết:

a) Trong mỗi hình vẽ có 10 ngôi sao.

Ta có $\frac{2}{5} = \frac{{2 \times 2}}{{5 \times 2}} = \frac{4}{{10}}$

Quan sát ta thấy hình B đã tô màu $\frac{4}{{10}}$ số ngôi sao hay $\frac{2}{5}$ số ngôi sao.

Chọn B.

b) Ta có: \(\frac{5}{6} = \frac{{5 \times 5}}{{6 \times 5}} = \frac{{25}}{{30}}\)

Chọn C

Câu 3

Tính

${\text{a) }}\frac{{5 \times 6 \times 12}}{{6 \times 12 \times 7}}{\text{ }}$

${\text{b) }}\frac{{9 \times 8 \times 15}}{{15 \times 9 \times 16}}$

Phương pháp giải:

Chia nhẩm cả tử số và mẫu số cho các thừa số chung.

Lời giải chi tiết:

${\text{a) }}\frac{{5 \times 6 \times 12}}{{6 \times 12 \times 7}}{\text{ = }}\frac{5}{7}$

${\text{b) }}\frac{{9 \times 8 \times 15}}{{15 \times 9 \times 16}} = \frac{{9 \times 8 \times 15}}{{15 \times 9 \times 8 \times 2}} = \frac{1}{2}$

Câu 1

Quy đồng mẫu số các phân số.

a) $\frac{1}{6}$ và $\frac{7}{{18}}$                                 

b) $\frac{4}{5}$ và $\frac{{11}}{{60}}$                                       

c) $\frac{7}{{25}}$ và $\frac{3}{{100}}$

Phương pháp giải:

- Xác định mẫu số chung.

- Tìm thương của mẫu số chung và mẫu số của phân số kia.

- Lấy thương tìm được nhân với tử số và mẫu số của phân số kia. Giữ nguyên phân số có mẫu số là mẫu số chung.

Lời giải chi tiết:

a) $\frac{1}{6}$ và $\frac{7}{{18}}$         

$\frac{1}{6} = \frac{{1 \times 3}}{{6 \times 3}} = \frac{3}{{18}}$            

b) $\frac{4}{5}$ và $\frac{{11}}{{60}}$                                       

$\frac{4}{5} = \frac{{4 \times 12}}{{5 \times 12}} = \frac{{48}}{{60}}$      

c) $\frac{7}{{25}}$ và $\frac{3}{{100}}$

$\frac{7}{{25}} = \frac{{7 \times 4}}{{25 \times 4}} = \frac{{28}}{{100}}$

Câu 2

Quy đồng mẫu số các phân số.

a) $\frac{2}{5};\,\,\frac{{13}}{{15}}$ và $\frac{{19}}{{45}}$                                                                        b) $\frac{1}{2};\,\,\frac{3}{8};\,\,\frac{5}{4}$và $\frac{7}{{16}}$

Phương pháp giải:

- Xác định mẫu số chung.

- Tìm thương của mẫu số chung và mẫu số của phân số kia.

- Lấy thương tìm được nhân với tử số và mẫu số của phân số kia. Giữ nguyên phân số có mẫu số là mẫu số chung.

Lời giải chi tiết:

a) $\frac{2}{5};\,\,\frac{{13}}{{15}}$ và $\frac{{19}}{{45}}$               

$\frac{2}{5} = \frac{{2 \times 9}}{{5 \times 9}} = \frac{{18}}{{45}}\,\,\,;\,\,\,\frac{{13}}{{15}} = \frac{{13 \times 3}}{{15 \times 3}} = \frac{{39}}{{45}}$                       

b) $\frac{1}{2};\frac{3}{8};\frac{5}{4}$và $\frac{7}{{16}}$

$\frac{1}{2} = \frac{{1 \times 8}}{{2 \times 8}} = \frac{8}{{16}}\,\,\,;\,\,\,\,\frac{3}{8} = \frac{{3 \times 2}}{{8 \times 2}} = \frac{6}{{16}}\,\,\,\,;\,\,\,\,\frac{5}{4} = \frac{{5 \times 4}}{{4 \times 4}} = \frac{{20}}{{16}}$

Câu 3

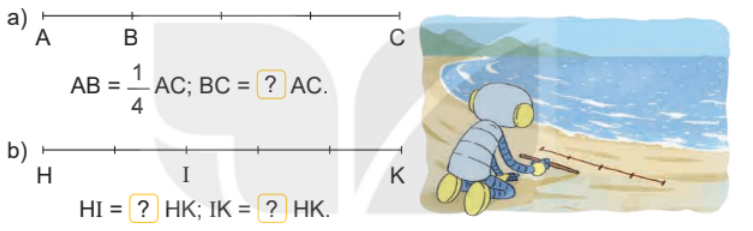
Tìm phân số thích hợp (theo mẫu).

Phương pháp giải:

Quan sát hình vẽ rồi viết phân số ứng với mỗi đoạn thẳng.

Lời giải chi tiết:

a) ${\text{BC}} = \frac{3}{4}{\text{AC}}$

b) ${\text{HI}} = \frac{2}{5}{\text{HK}}\,\,\,\,\,{\text{;   IK}} = \frac{3}{5}{\text{HK}}$

Câu 4

Viết 2 ; $\frac{1}{6};\frac{3}{4}$ thành ba phân số đều có mẫu số là 12.

Phương pháp giải:

Bước 1: Lấy 12 chia cho mẫu số của các phân số đã cho.

Bước 2: Nhân cả tử số và mẫu số của phân số đã cho với số vừa tìm được ở bước 1.

Lời giải chi tiết:

$\frac{3}{4} = \frac{{3 \times 3}}{{4 \times 3}} = \frac{9}{{12}}$

Vậy ba phân số tìm được là: $\frac{{24}}{{12}};\,\,\frac{2}{{12}};\,\,\frac{9}{{12}}$.

Câu 5

Đố em?

Em hãy cùng Mai tìm cách giúp Nam

Phương pháp giải:

Gập đoạn dây để chia đều đoạn dây thành 4 phần và cắt lấy 1 phần.

Lời giải chi tiết:

Ta gập đôi đoạn dây sao cho hai đầu dây trùng với nhau. Lúc này sợi dây được chia thành 2 đoạn dài bằng nhau.

Tiếp tục gập đôi đoạn dây một lần nữa. Lúc này sợi dây ban đầu được chia thành 4 đoạn dài bằng nhau.

Cắt 1 phần đoạn dây vừa gập ta được đoạn dây dài $\frac{1}{4}$m.

Câu 1

> , < , = ?

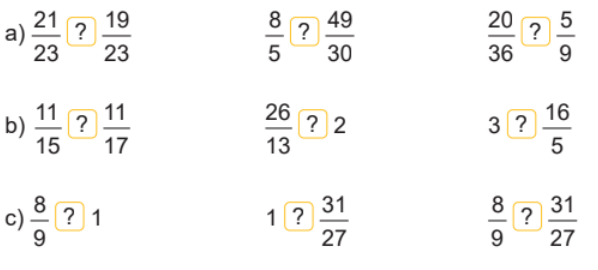
Phương pháp giải:

- Trong hai phân số cùng mẫu số: Phân số nào có tử số lớn hơn thì lớn hơn.

- Muốn so sánh hai phân số khác mẫu số, ta có thể quy đồng mẫu số hai phân số đó, rồi so sánh các tử số của hai phân số mới.

- So sánh phân số với 1:

• Nếu tử số bé hơn mẫu số thì phân số bé hơn 1.

• Nếu tử số lớn mẫu số thì phân số lớn hơn 1.

• Nếu tử số bằng mẫu số thì phân số bằng 1.

Lời giải chi tiết:

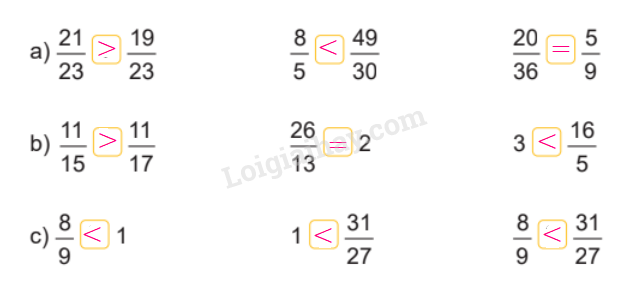
Câu 2

Đ, S?

a) Rô-bốt nói: Mình được Mai cho nhiều bi hơn Việt ......

b) Việt nói: Mình được Mai cho nhiều bi hơn Rô-bốt ......

Phương pháp giải:

So sánh hai phân số $\frac{1}{3}$ và $\frac{4}{9}$ để trả lời câu hỏi.

Lời giải chi tiết:

Ta có: $\frac{1}{3} = \frac{3}{9} < \frac{4}{9}$. Vậy

a) Rô-bốt nói: Mình được Mai cho nhiều bi hơn Việt.       S

b) Việt nói: Mình được Mai cho nhiều bi hơn Rô-bốt.      Đ

Câu 3

Chọn câu trả lời đúng.

Có một cái bánh pi-da, Việt ăn $\frac{1}{2}$ cái bánh, Mi ăn $\frac{1}{6}$ cái bánh, Mai ăn $\frac{1}{3}$ cái bánh. Bạn nào ăn ít bánh nhất?

A. Việt                                               

B. Mi                                                  

C. Mai

Phương pháp giải:

So sánh các phân số chỉ phần bánh 3 bạn đã ăn để trả lời câu hỏi.

Lời giải chi tiết:

$\frac{1}{2} = \frac{3}{6}\,\,\,;\,\,\,\frac{1}{3} = \frac{2}{6}$

Ta có $\frac{1}{6} < \frac{1}{3} < \frac{1}{2}$ nên bạn Mi ăn ít bánh nhất.

Chọn B

Câu 4

Hãy sắp xếp các phân số ở trong hàng rào theo thứ tự từ bé đến lớn.

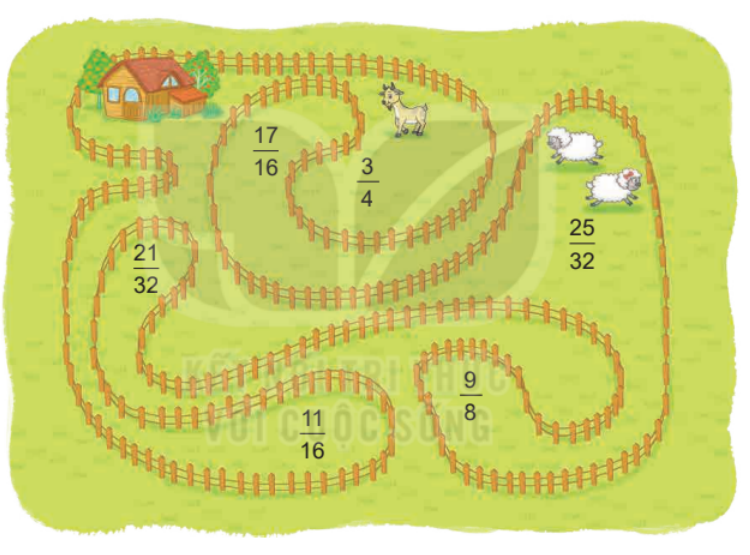
Phương pháp giải:

So sánh các phân số đã cho rồi sắp xếp theo thứ tự từ bé đến lớn.

Lời giải chi tiết:

Chọn mẫu số chung là 32

$\frac{{17}}{{16}} = \frac{{34}}{{32}}\,\,;\,\,\,\frac{3}{4} = \frac{{24}}{{32}}\,\,\,\,;\,\,\,\,\frac{{11}}{{16}} = \frac{{22}}{{32}}\,\,\,\,;\,\,\,\,\frac{9}{8} = \frac{{36}}{{32}}$

Ta có$\frac{{21}}{{32}} < \frac{{22}}{{32}} < \frac{{24}}{{32}} < \frac{{25}}{{32}} < \frac{{34}}{{32}} < \frac{{36}}{{32}}$ nên $\frac{{21}}{{32}} < \frac{{11}}{{16}} < \frac{3}{4} < \frac{{25}}{{32}} < \frac{{17}}{{16}} < \frac{9}{8}$

Vậy các phân số ở trong hàng rào theo thứ tự từ bé đến lớn là: $\frac{{21}}{{32}};\,\,\frac{{11}}{{16}};\,\,\frac{3}{4};\,\,\frac{{25}}{{32}};\,\,\frac{{17}}{{16}};\,\,\frac{9}{8}$

Câu 5

Đố em!

Bờm có quả bưởi cân nặng $\frac{9}{8}$ kg. Cuội có quả thanh long cân nặng $\frac{{31}}{{32}}$kg. Cuội khoe rằng quả của mình nặng hơn quả của Bờm. Không quy đồng mẫu số, em hãy cho biết Cuội nói đúng hay sai.

Phương pháp giải:

Sử dụng cách so sánh phân số với 1 để trả lời yêu cầu đề bài.

Lời giải chi tiết:

Ta có: $\frac{9}{8} > 1\,\,\,;\,\,\,\frac{{31}}{{32}} < 1$ nên $\frac{9}{8} > \frac{{31}}{{32}}$

Vậy Cuội nói sai.