Phương pháp giải bài tập tổng hợp hai dao động điều hòa cùng phương, cùng tần số

Phương pháp giải bài tập tổng hợp hai dao động điều hòa cùng phương, cùng tần số

Khi vật tham gia đồng thời nhiều dao động cùng tần số thì dao động của vật là dao động tổng hợp. Giả sử một vật tham gia đồng thời hai dao động:

+ \({x_1} = {A_1}\cos \left( {\omega t + {\varphi _1}} \right)\)

+ \({x_2} = {A_2}\cos \left( {\omega t + {\varphi _2}} \right)\)

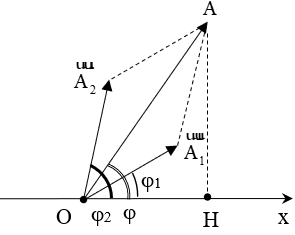
Ta lần lượt vẽ hai vecto quay đặc trưng cho hai dao động.

Khi đó, dao động tổng hợp có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\)

- Nếu cùng biên độ thì cộng lượng giác: \(x = {x_1} + {x_2}\)

- Nếu biên độ khác nhau thì nên sử dụng biểu diễn vecto quay để tổng hợp các dao động cùng phương, cùng tần số.

* Phương pháp vecto quay:

\({A^2} = A_1^2 + A_2^2 + 2{{\rm{A}}_1}{A_2}\cos \left( {{\varphi _2} - {\varphi _1}} \right)\)

\(\tan \varphi  = \dfrac{{{A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}}}{{{A_1}\cos {\varphi _1} + {A_2}\cos {\varphi _2}}}\)

- Nếu hai vecto:

+ Cùng pha: \({A_{\max }} = {A_1} + {A_2},\varphi  = {\varphi _1} = {\varphi _2}\)

+ Ngược pha: \({A_{\min }} = \left| {{A_1} - {A_2}} \right|\), \(\left\{ \begin{array}{l}{A_1} > {A_2} \Rightarrow \varphi  = {\varphi _1}\\{A_1} < {A_2} \Rightarrow \varphi  = {\varphi _2}\end{array} \right.\)

+ Vuông pha: \({A^2} = A_1^2 + A_2^2\)

+ Khi A₁ và A₂ xác định, \({\varphi _1},{\varphi _2}\) chưa biết, ta luôn có: \(\left| {{A_1} - {A_2}} \right| \le A \le {A_1} + {A_2}\)

* Sử dụng máy tính giải bài toán tổng hợp phương trình dao động:

Bài tập ví dụ:

Bài 1: Một vật thực hiện đồng thời hai dao động điều hòa \(\left\{ \begin{array}{l}{x_1} = 6\cos 4\pi t\left( {cm} \right)\\{x_2} = 6\cos \left( {4\pi t + \frac{\pi }{3}} \right)\left( {cm} \right)\end{array} \right.\). Hãy xác định dao động tổng hợp của hai dao động trên.

Hướng dẫn giải

Ta có: dao động tổng hợp có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\left( {cm} \right)\)

+ Biên độ A:

\(A = \sqrt {A_1^2 + A_2^2 + 2{{\rm{A}}_1}{A_2}\cos \left( {{\varphi _2} - {\varphi _1}} \right)}\\  = \sqrt {{6^2} + {6^2} + 2.6.6.\cos \left( {\frac{\pi }{3} - 0} \right)}  = 6\sqrt 3 \left( {cm} \right)\)

+ \(\tan \varphi  = \dfrac{{{A_1}\sin {\varphi _1} + {A_2}\sin {\varphi _2}}}{{{A_1}\cos {\varphi _1} + {A_2}\cos {\varphi _2}}} \\= \dfrac{{6\sin 0 + 6\sin \dfrac{\pi }{3}}}{{6\cos 0 + 6\cos \dfrac{\pi }{3}}} = \dfrac{{\sqrt 3 }}{3}\)

\( \Rightarrow \varphi  = \frac{\pi }{6}\)

Vậy dao động tổng hợp của hai dao động trên là:

\(x = 6\sqrt 3 \cos \left( {4\pi t + \frac{\pi }{6}} \right)\left( {cm} \right)\)

Bài 2: Một vật thực hiện đồng thời hai dao động điều hòa với biên dộ lần lượt là 3 cm và 5 cm. Trong các giá trị sau, giá trị nào không thể là biên độ của dao động tổng hợp?

A. 4 cm            B. 5 cm            C. 3 cm            D. 10 cm

Hướng dẫn giải

Ta có: \(\left| {{A_1} - {A_2}} \right| \le A \le {A_1} + {A_2}\)

\( \Leftrightarrow \left| {3 - 5} \right| \le A \le 3 + 5 \Leftrightarrow 2 \le A \le 8\)

Vậy 10 cm không thể là biên độ của dao động tổng hợp.

Chọn D.