Lý thuyết Tổng hợp hai dao động điều hòa cùng phương, cùng tần số - Phương pháp giản đồ FRE-NEN
Mỗi dao động điều hòa được biểu diễn bằng một vectơ quay.
TỔNG HỢP HAI DAO ĐỘNG ĐIỀU HÒA CÙNG PHƯƠNG, CÙNG TẦN SỐ
PHƯƠNG PHÁP GIẢN ĐỒ FRE-NEN
1. Mỗi dao động điều hòa được biểu diễn bằng một vectơ quay. Véc tơ này có gốc tại gốc tọa độ của trục Ox, có độ dài bằng biên độ dao động A và hợp với trục Ox một góc bằng pha ban đầu \(\varphi\)
2. Phương pháp giản đồ Fre-nen: Lần lượt vẽ hai vec tơ quay biểu diễn hai phương trình dao động thành phần. Vectơ tổng của hai vectơ thành phàn biểu diễn phương trình của dao động tổng hợp (Hình 5.1).
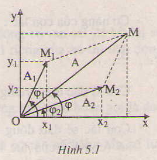
3. Nếu một vật tham gia đồng thời hai dao động điều hòa cùng phương, cùng tần số với các phương trình:
\(x_1=A_1 cos(ωt + \varphi _{1}\)) và \(x_2=A_2 cos(ωt + \varphi _{2}\))
Thì dao động tổng hợp sẽ là: \(x = x_1 + x_2 = Acos(ωt + \varphi\)) với A và \(\varphi\) được xác định bởi:
\({A^2} = A_1^2 + A_2^2 + 2{A_1}{A_2}{\rm{cos}}\left( {{\varphi _2} - {\varphi _1}} \right)\)
\(tan\varphi =\dfrac{A_{1}sin\varphi _{1}+A_{2}sin\varphi _{2}}{A_{1}cos\varphi _{1}+A_{2}sos\varphi _{2}}.\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Lý thuyết Tổng hợp hai dao động điều hòa cùng phương, cùng tần số - Phương pháp giản đồ FRE-NEN timdapan.com"







