Lý thuyết Mở đầu về đường tròn Toán 9 Kết nối tri thức
1. Đường tròn
1. Đường tròn
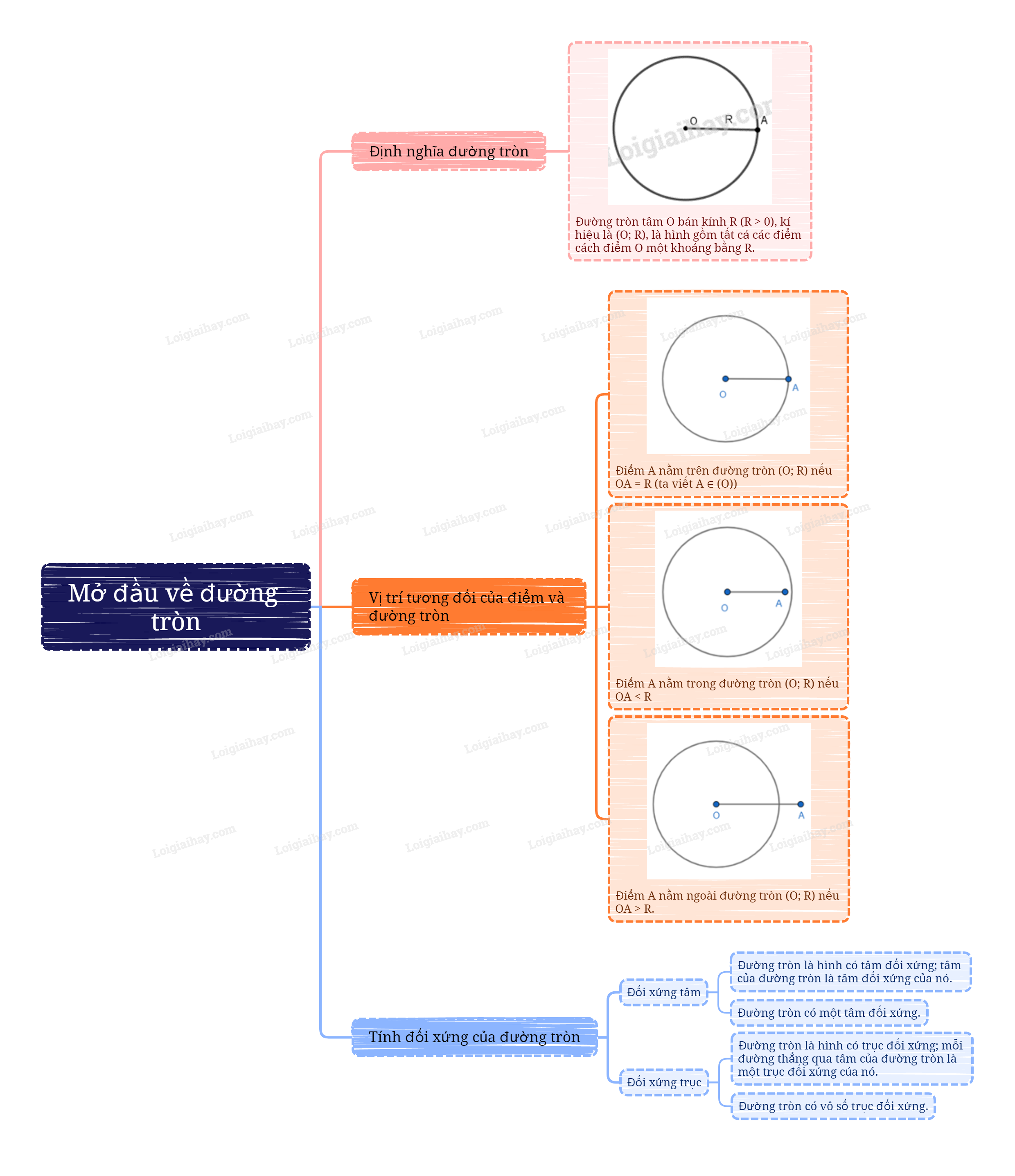
Định nghĩa đường tròn
|
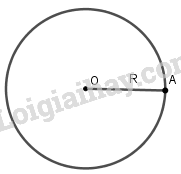
Đường tròn tâm O bán kính R (R > 0), kí hiệu là (O; R), là hình gồm tất cả các điểm cách điểm O một khoảng bằng R. |
Khi không cần để ý đến bán kính ta kí hiệu đường tròn tâm O là (O).
Điểm thuộc đường tròn
Nếu A là một điểm của đường tròn (O) thì ta viết \(A \in \left( O \right)\). Khi đó, ta còn nói đường tròn (O) đi qua điểm A, hay điểm A nằm trên đường tròn (O).
Tổng quát:
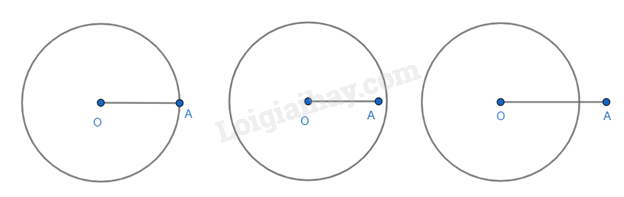
- Điểm A nằm trên đường tròn (O; R) nếu OA = R;
- Điểm A nằm trong đường tròn (O; R) nếu OA < R;
- Điểm A nằm ngoài đường tròn (O; R) nếu OA > R.
Hình tròn tâm O bán kính R là hình gồm các điểm nằm trên và nằm trong đường tròn (O;R).
2. Tính đối xứng của đường tròn
a) Đối xứng tâm
Hai điểm M và M’ gọi là đối xứng với nhau qua điểm I (hay qua tâm I) nếu I là trung điểm của đoạn MM’.

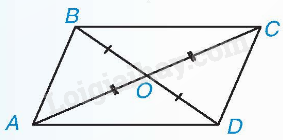
Ví dụ: Nếu O là giao điểm của hai đường chéo của hình bình hành ABCD thì
+) OA = OC nên A và C đối xứng với nhau.
+) OB = OD nên B và D đối xứng với nhau.
b) Đối xứng trục
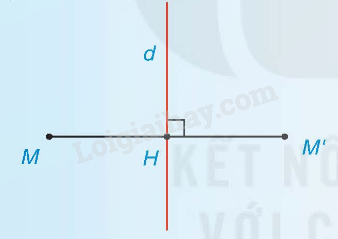
Hai điểm M và M’ gọi là đối xứng với nhau qua đường thẳng d (hay qua trục d) nếu d là đường trung trực của đoạn MM’.
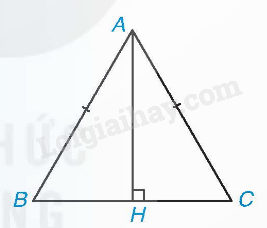
Ví dụ: Nếu AH là đường cao trong tam giác ABC cân tại A thì AH cũng là đường trung trực của BC, nên B và C đối xứng với nhau qua AH.
c) Tâm đối xứng của đường tròn
|
- Đường tròn là hình có tâm đối xứng; tâm của đường tròn là tâm đối xứng của nó. - Đường tròn có một tâm đối xứng. |
d) Trục đối xứng của đường tròn
|
- Đường tròn là hình có trục đối xứng; mỗi đường thẳng qua tâm của đường tròn là một trục đối xứng của nó. - Đường tròn có vô số trục đối xứng. |
Search google: "từ khóa + timdapan.com" Ví dụ: "Lý thuyết Mở đầu về đường tròn Toán 9 Kết nối tri thức timdapan.com"