Lý thuyết Khi nào góc xOy + góc yOz = góc xOz?

 1. Tính chất cộng số đo hai góc

Nếu tia \(Oy\) nằm giữa tia \(Ox\) và tia \(Oz\) thì  \(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\). 

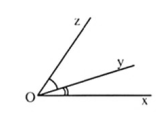
Ngược lại, nếu  \(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\) thì tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Oz.\)

Lưu ý:  

a) Ta có thể dùng mệnh đề tương đương sau với tính chất trên:

Nếu \(\widehat{xOy}+\widehat{yOz}\neq \widehat{xOz}\) thì tia \(Oy\) không nằm giữa hai tia \(Ox\) và \(Oz.\)

b) Cộng liên tiếp. Nếu tia \(Oy\) nằm giữa hai tia \(Ox\) và \(Ot;\) tia \(Oz\) nằm giữa hai tia \(Oy\) và \(Ot\) thì:

\(\widehat{xOy}+\widehat{yOz}+ \widehat{tO z}=\widehat{xOt}\)

2. Hai góc kề nhau, phụ nhau, bù nhau

-Hai góc kề nhau  là hai góc có một cạnh chung và hai cạnh còn lại nằm trên hai nữa mặt phẳng đối nhau bờ chứa cạnh chung.

- Hai góc phụ nhau là hai góc có tổng số đo bằng \(90^{0}\)

- Hai góc bù nhau là hai góc có tổng số đo bằng \(180^{0}\)

Lưu ý:

a) Hai góc kề bù là hai góc vừa kề nhau vừa bù nhau. Hai góc kề bù có tổng số đo bằng \(180^{0}\) .

b) Hai góc cùng phụ (hoặc cùng bù) với một góc thứ 3 thì bằng nhau.