Lý thuyết Định lí Thalès trong tam giác SGK Toán 8 - Cánh diều
Định lí Thalès là gì?
1. Đoạn thẳng tỉ lệ
Hai đoạn thẳng AB và CD gọi là tỉ lệ với hai đoạn thẳng MN và PQ nếu có tỉ lệ thức: \(\frac{{AB}}{{CD}} = \frac{{MN}}{{PQ}}\)
2. Định lí Thalès
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó định ra trên hai cạnh đó những đoạn thẳng tương ứng tỉ lệ.
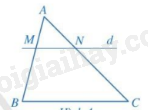
\(\begin{array}{l}\Delta ABC,MN//BC(M \in AB,N \in AC)\\ \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}};\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}};\frac{{BM}}{{AB}} = \frac{{NC}}{{AC}}\end{array}\)
3. Định lí Thalès đảo
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
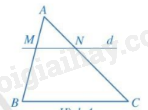
\(\Delta ABC,M \in AB,N \in AC,\frac{{AM}}{{MB}} = \frac{{AN}}{{NC}} \Rightarrow MN//BC\)
4. Hệ quả của định lí Thalès
Nếu một đường thẳng song song với một cạnh của tam giác và cắt hai cạnh còn lại thì nó tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
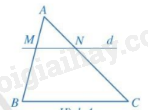
\(\begin{array}{l}\Delta ABC,MN//BC(M \in AB,N \in AC)\\ \Rightarrow \frac{{AM}}{{AB}} = \frac{{AN}}{{AC}} = \frac{{MN}}{{BC}}\end{array}\)
Chú ý. Hệ quả vẫn đúng cho trường hợp đường thẳng d song song với một cạnh của tam giác và cắt phần kéo dài của hai cạnh còn lại.

Search google: "từ khóa + timdapan.com" Ví dụ: "Lý thuyết Định lí Thalès trong tam giác SGK Toán 8 - Cánh diều timdapan.com"







