Lý thuyết Đa thức nhiều biến SGK Toán 8 - Cùng khám phá
Đa thức là gì?
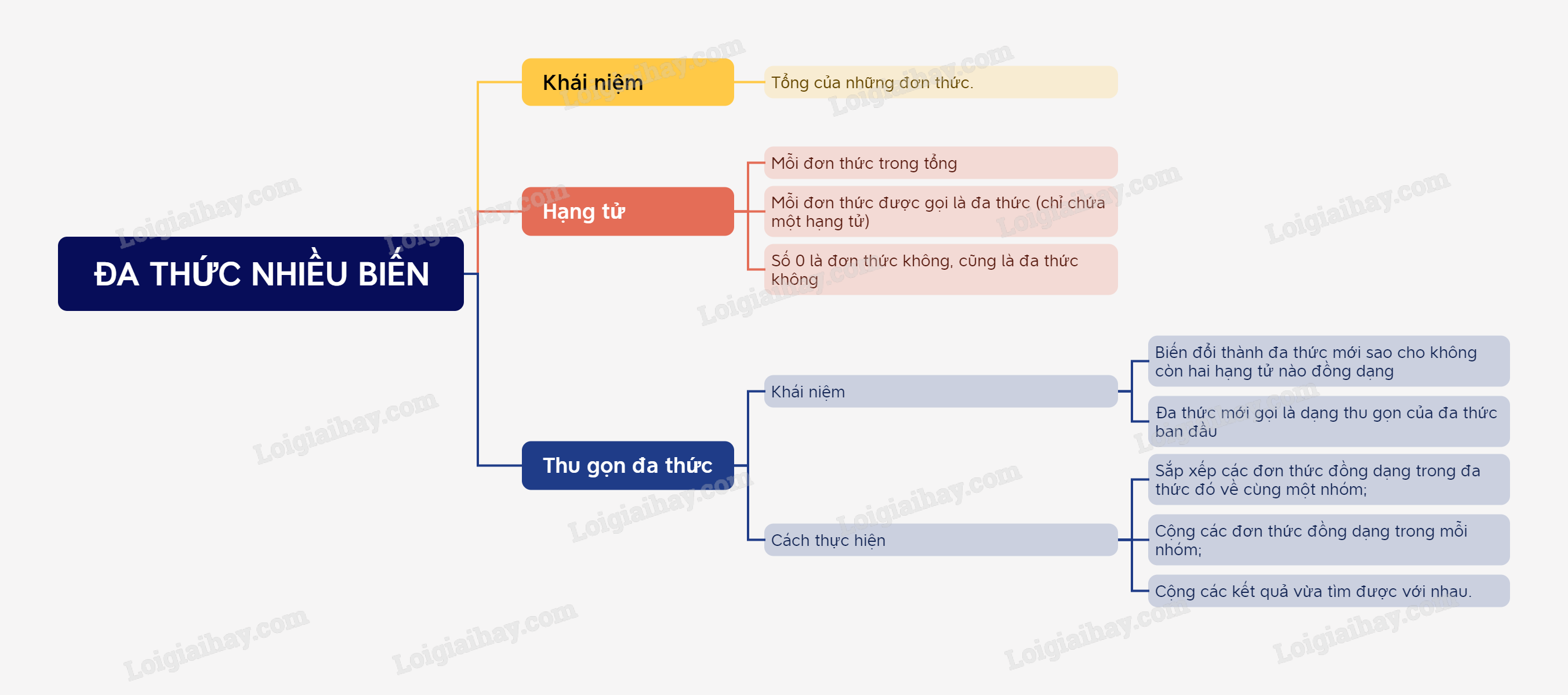
1. Khái niệm
- Đa thức là một tổng của những đơn thức.
- Mỗi đơn thức trong tổng gọi là một hạng tử của đa thức đó.
Chú ý: mỗi đơn thức được gọi là một đa thức (chỉ chứa một hạng tử).
Số 0 được gọi là đơn thức không, cũng gọi là đa thức không.
Ví dụ:
\({x^2} - 4x + 3;{x^2}\; + {\rm{ }}3xy{z^2}\; - {\rm{ }}yz{\rm{ }} + {\rm{ }}1;\left( {x{\rm{ }} + {\rm{ }}3y} \right){\rm{ }} + \left( {2x{\rm{ }}--{\rm{ }}y} \right)\) là đa thức.
\(\frac{{x + y}}{{x - y}},\frac{{{x^2} + 2}}{{{x^2} - {y^2}}}\) không phải là đa thức.
\({x^2} - 4x + 3\)có 3 hạng tử \({x^2}; - 4x;3\).
\({x^2}\; + {\rm{ }}3xy{z^2}\; - {\rm{ }}yz{\rm{ }} + {\rm{ }}1\) có 4 hạng tử \({x^2}{\rm{; }}3xy{z^2};\; - {\rm{ }}yz{\rm{ ; }}1\).
2. Thu gọn đa thức
- Thu gọn đa thức P là viết đa thức này thành đa thức Q sao cho trong đa thức Q không còn hai hạng tử nào đồng dạng. Đa thức Q gọi là dạng thu gọn của đa thức P.
- Cách thu gọn đa thức
Để thu gọn một đa thức, ta làm như sau:
+ Sắp xếp các đơn thức đồng dạng trong đa thức đó về cùng một nhóm;
+ Cộng các đơn thức đồng dạng trong mỗi nhóm;
+ Cộng các kết quả vừa tìm được với nhau.
Ví dụ:
\(\begin{array}{l}A = {x^3} - 2{x^2}y - {x^2}y + 3x{y^2} - {y^3}\\\,\,\,\,\, = {x^3} - 3{x^2}y - 3x{y^2} - {y^3}\end{array}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Lý thuyết Đa thức nhiều biến SGK Toán 8 - Cùng khám phá timdapan.com"







