Lý thuyết ảnh của một vật tạo bởi thấu kính hội tụ
Đối với thấu kính hội tụ:
ẢNH CỦA MỘT VẬT TẠO BỞI THẤU KÍNH HỘI TỤ
I - Đặc điểm của ảnh của một vật tạo bởi thấu kính hội tụ
|
Khoảng cách từ vật đến thấu kính (d) |
Đặc điểm của ảnh |
|
|
Vị trí ảnh (d’) \(\left( {CO = C'O = 2OF} \right)\) |
Tính chất ảnh |
|
|
Vật ở rất xa thấu kính |
\(d' = {\rm{OF'}}\) |
ảnh thật |
|
\(d > 2f\) |
ảnh ở \(F'C'\) |
ảnh thật ngược chiều với vật và nhỏ hơn vật |
|
\(d = 2f\) |
ảnh ở C’ ( với \(OC' = 2{\rm{OF}}\)) |
ảnh thật ngược chiều với vật và bằng vật |
|
\(f < d < 2f\) |
từ \(C'\) đến \(\infty \) |
ảnh thật ngược chiều với vật và lớn hơn vật |
|
\(d = f\) |
ở \(\infty \) |
không cho ảnh
|
|
\(d < f\) |
trước thấu kính |
ảnh ảo, cùng chiều với vật và lớn hơn vật |
II - Cách dựng ảnh
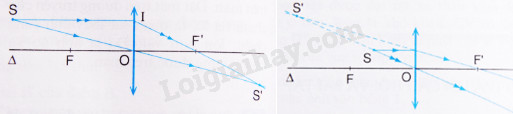
1. Dựng ảnh của điểm sáng S tạo bởi thấu kính hội tụ
- Từ \(S\) ta dựng hai trong ba tia đặc biệt đến thấu kính sau đó vẽ hai tia ló ra khỏi thấu kính
- Nếu 2 tia ló cắt nhau thì giao điểm cắt nhau đó chính là ảnh thật \(S'\) của \(S\), nếu đường kéo dài của hai tia ló cắt nhau thì giao điểm cắt nhau đó chính là ảnh ảo \(S'\) của \(S\) qua thấu kính.
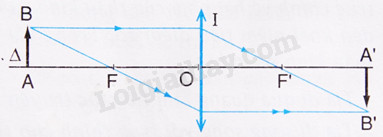
2. Dựng ảnh của một vật sáng AB tạo bởi thấu kính hội tụ
- Muốn dựng ảnh \(A'B'\) của \(AB\) qua thấu kính (\(AB\) vuông góc với trục chính, \(A\) nằm trên trục chính), chỉ cần dựng ảnh \(B'\) của \(B\) bằng cách vẽ đường truyền của hai trong ba tia sáng đặc biệt, sau đó từ \(B'\) hạ vuông góc xuống trục chính là ta có ảnh \(A'\) của \(A\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Lý thuyết ảnh của một vật tạo bởi thấu kính hội tụ timdapan.com"







