Bài C5 trang 117 SGK Vật lí 9
Giải bài C5 trang 117 SGK Vật lí 9. Vật sáng AB được đặt vuông góc
Đề bài
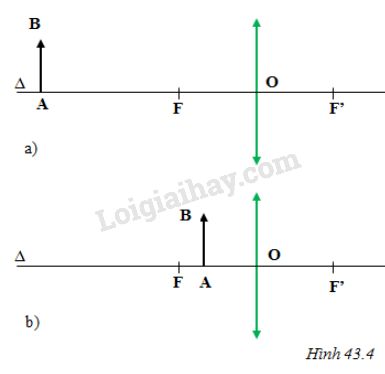
Vật sáng AB được đặt vuông góc với trục chính của thấu kính hội tụ có tiêu cự f = 12cm. Điểm A nằm trên trục chính. Hãy dựng ảnh A'B' của AB và nhận xét đặc điểm của ảnh A'B' trong hai trường hợp:
+ Vật AB cách thấu kính một khoảng d = 36cm (hình 43.4a)
+ Vật AB cách thấu kính một khoảng d = 8cm (hình 43.4b)
Phương pháp giải - Xem chi tiết
Đường truyền của ba tia sáng đặc biệt qua thấu kính hội tụ:
- Tia tới đến quang tâm thì tia ló tiếp tục truyền thẳng theo phương của tia tới.
- Tia tới song song với trục chính thì tia ló qua tiêu điểm.
- Tia tới qua tiêu điểm thì tia ló song song với trục chính.
Lời giải chi tiết
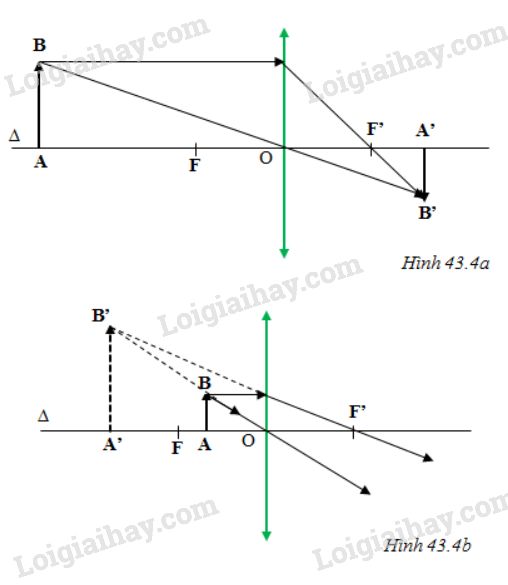
Xét trường hợp hình 43.4a
Ta có: \(\left\{ \begin{array}{l}OF = OF' = f = 12cm\\OA = d = 36cm\end{array} \right.\)
Đặt \(A'O = d'\)
Ta có: \(\Delta ABO \sim \Delta A'B'O\)
Ta suy ra: \(\dfrac{{AO}}{{A'O}} = \dfrac{{AB}}{{A'B'}} \Leftrightarrow \dfrac{d}{{d'}} = \dfrac{{AB}}{{A'B'}}\) (1)
Lại có: \(\Delta A'B'F' \sim \Delta OIF'\)
Ta suy ra: \(\dfrac{{A'B'}}{{OI}} = \dfrac{{A'F'}}{{OF'}} \Leftrightarrow \dfrac{{A'B'}}{{AB}} = \dfrac{{A'O - OF'}}{{OF'}} = \dfrac{{d' - f}}{f}\) (1)
Từ (1) và (2) ta suy ra:
\(\begin{array}{l}\dfrac{d}{{d'}} = \dfrac{f}{{d' - f}}\\ \Rightarrow d = \dfrac{{d'f}}{{d' - f}}\\ \Leftrightarrow \dfrac{1}{d} = \dfrac{{d' - f}}{{d'f}} = \dfrac{1}{f} - \dfrac{1}{{d'}}\\ \Rightarrow \dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d'}}\end{array}\)
Chú ý: Công thức \(\dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d'}}\) dùng để xác định tiêu cự, khoảng cách từ vật đến thấu kính, khoảng cách từ ảnh đến thấu kính khi biết 2 trong 3 giá trị đó.
(d – khoảng cách từ vật đến thấu kính, d’ – khoảng cách từ ảnh đến thấu kính)
Với \(d > 0\)- vật thật, \(d < 0\) vật ảo, \(d' > 0\) - ảnh thật, \(d' < 0\) - ảnh ảo
Với \(\dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d'}} \Rightarrow d' = \dfrac{{df}}{{d - f}} = \dfrac{{36.12}}{{36 - 12}} = 18cm\)
=> Ảnh A’B’ là ảnh thật, ngược chiều với vật và cách thấu kính một khoảng \(18cm\)
Tương tự với hình 43.4b
Ta cũng có \(\dfrac{1}{f} = \dfrac{1}{d} + \dfrac{1}{{d'}}\)
Ta suy ra: \(d' = \dfrac{{df}}{{d - f}} = \dfrac{{8.12}}{{8 - 12}} = - 24cm\)
=> A’B’ là ảnh ảo lớn hơn vật, cùng chiều với vật và cách thấu kính một khoảng \(24cm\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài C5 trang 117 SGK Vật lí 9 timdapan.com"







