Luyện tập 3 trang 153 Tài liệu dạy – học Toán 8 tập 1
Giải bài tập Chứng minh rằng trong một ngũ giác, tổng các đường chéo lớn hơn chu vi.
Đề bài
Chứng minh rằng trong một ngũ giác, tổng các đường chéo lớn hơn chu vi.
Lời giải chi tiết
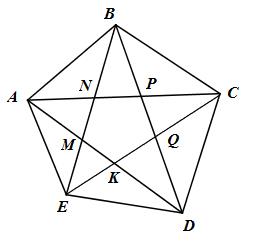
Xét ngũ giác ABCDE cần chứng minh rằng:
\(AC + A{\rm{D}} + BD + BE + CE > AB + BC + CD + DE + EA\)
Gọi M, N lần lượt là giao điểm của BE và AD, AC.
P, Q lần lượt là giao điểm của BD với AC, CE.
K là giao điểm của CE và AD.
\(\Delta NAB\) có \(AN + BN > AB\) (BĐT tam giác)
Tương tự \(\Delta PBC\) có \(BP + CP > BC,\,\,\Delta QCD\) có \(CQ + DQ > CD\)
\(\Delta KDE\) có \(DK + EK > DE,\,\,\Delta MAE\) có \(AM + EM > EA\)
Do đó \(AN + BN + BP + CP + CQ + DQ + DK + EK + AM + EM > AB + BC + CD + DE + EA\)
Mà
\(\eqalign{ & AC + AD + BD + BE + CE \cr & > \left( {AN + CP} \right) + \left( {DK + AM} \right) + \left( {BP + DQ} \right) + \left( {EM + BN} \right) + \left( {CQ + EK} \right) \cr & = AN + CP + DK + AM + BP + DQ + EM + BN + CQ + EK \cr & = AN + BN + BP + CP + CQ + DQ + DK + EK + AM + EM \cr} \)
Vậy \(AC + A{\rm{D}} + BD + BE + CE > AB + BC + CD + DE + EA\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Luyện tập 3 trang 153 Tài liệu dạy – học Toán 8 tập 1 timdapan.com"