Hoạt động 8 trang 114 Tài liệu dạy – học Toán 8 tập 1

Đề bài

Điền vào chỗ trống để chứng mình trong hình bình hành các cạnh đối bằng nhau, các góc đối bằng nhau và hai đường chéo cắt nhau tại trung điểm của mỗi đường.

a) Hình bình hành ABCD là hình thang có hai cạnh bên AD, BC song song với nhau nên AD = …; … = CD.

b) \(\Delta ABC = \Delta CDA(c.c.c)\) suy ra : \(\widehat B = ...\) .

Chứng mình tương tự, ta cũng có : \(... = \widehat C\) (h.16).

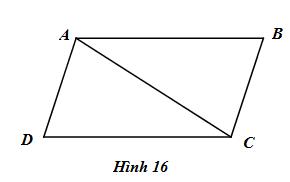
c) Xét \(\Delta AOB\) và \(\Delta COD\) (h.17) có:

AB = ….. ( cạnh đối hình bình hành)

\(...... = \widehat {{C_1}}\) (So le trong, AB//CD)

\(\widehat {{B_1}} = ......\) (So le trong, AB//CD).

Do đó \(\Delta AOB = \Delta COD(g.c.g)\) , Suy ra: OA = …… và …… = OD.

Lời giải chi tiết

a) Hình bình hành ABCD là hình thang có hai cạnh bên AD, BC song song với nhau nên \(AD = BC,\,\,AB = CD\).

b) \(\Delta ABC = \Delta CDA\,\,\left( {c.c.c} \right) \Rightarrow \widehat B = \widehat D\).

Chứng minh tương tự, ta cũng có: \(\widehat A = \widehat C\) (h.16)

c) Xét \(\Delta AOB\) và \(\Delta COD\) (h.17) có:

\(AB = CD\) (cạnh đối hình bình hành)

\(\widehat {{A_1}} = \widehat {{C_1}}\) (so le trong, AB // CD)

\(\widehat {{B_1}} = \widehat {{D_1}}\) (so le trong, AB // CD)

Do đó \(\Delta AOB = \Delta COD\,\,\left( {g.c.g} \right) \Rightarrow OA = OC\) và \(OB = OD\).