Bài 3. Giao thoa sóng trang 48, 49, 50, 51, 52, 53 Vật Lí 11 Cánh diều

KĐ

Một quả cầu chạm nhẹ mặt nước thì khi quả cầu dao động, mỗi điểm trên mặt nước sẽ dao động khi nhận được sóng truyền đến (Hình 3.1a)

Nhưng khi cho hai quả cầu chạm mặt nước và dao động đồng thời thì lại có những điểm đứng yên dù nhận được sóng từ hai nguồn truyền đến (Hình 3.1b).

Tại sao lại có những điểm đứng yên đó?

Phương pháp giải:

Dựa vào những kiến thức đã học về dao động và sóng lan truyền để giải thích.

Lời giải chi tiết:

Mỗi nguồn sóng phát ra một sóng, các điểm trên mặt nước dao động khi có sóng truyền đến. Khi hai nguồn cùng phát ra sóng, tại một số điểm có hai dao động truyền từ hai nguồn là ngược pha với nhau, triệt tiêu nhau hoàn toàn, khiến cho những điểm đó đứng yên.  

CH 1

Điểm M nằm cách đều hai nguồn sóng cùng tần số 90 Hz thì có thuộc hệ vân giao thoa của hai sóng đó không?

Phương pháp giải:

Điểm M nằm cách đều hai nguồn sóng thì \({x_1} - {x_2} = MA - MB = 0\).

Lời giải chi tiết:

Hai nguồn sóng có cùng tần số, nên hai nguồn này là hai nguồn kết hợp. M nằm cách đều hai nguồn nên MA = MB. Ta có \({x_2} - {x_1} = MB - MA = 0 \Rightarrow {x_2} - {x_1} = k\lambda (k = 0)\). Do đó, M thuộc hệ vân giao thoa.

CH 2

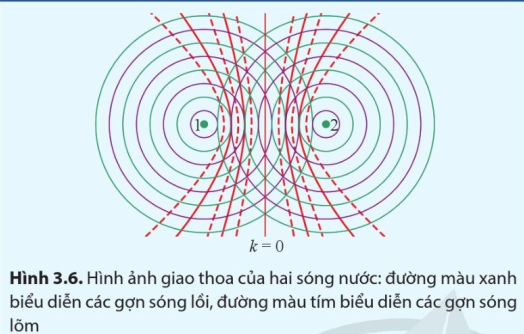
Biết bước sóng là khoảng cách giữa hai gợn lồi hoặc hai gợn lõm liên tiếp trên cùng một phương truyền sóng. Hãy nêu cách xác định bước sóng do hai nguồn phát ra trên Hình 3.6.

Phương pháp giải:

Sử dụng gợi ý bước sóng là khoảng cách giữa hai gợn lồi hoặc hai gợn lõm liên tiếp trên cùng một phương truyền sóng.

Lời giải chi tiết:

Dùng bút chì kẻ một đường thẳng đi qua nguồn sóng, ta biểu diễn được một phương truyền sóng. Chọn hai điểm là giao điểm của đường thẳng với hai đường tròn màu xanh (gợn sóng lồi) hoặc hai đường tròn màu tím (gợn sóng lõm) liên tiếp. bước sóng là độ dài của đoạn thẳng nối hai điểm này.  

CH 1

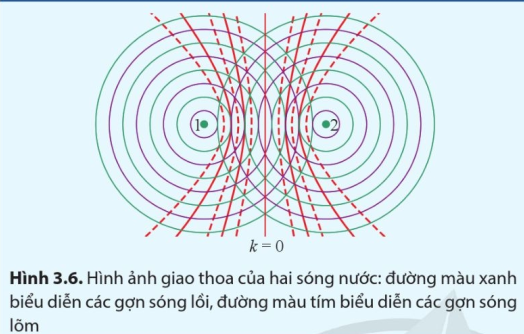
Dùng bút chì vẽ đường nối các điểm giao nhau giữa các gợn lồi hoặc của các gợn lõm của hai nguồn sóng trên Hình 3.6 và đối chiếu kết quả với công thức (3.1).

Phương pháp giải:

Nối các điểm giao nhau giữa các gợn lồi hoặc của các gợn lõm của hai nguồn sóng với hai nguồn và so sánh kết quả với công thức

Lời giải chi tiết:

Nối các điểm giao nhau giữa các gợn lồi hoặc của các gợn lõm của hai nguồn sóng với mỗi nguồn, đo khoảng cách x₁, x₂. Tính \(\frac{{{x_2} - {x_1}}}{\lambda }\) với \(\lambda \)được xác định trong câu hỏi trước. Nếu thương số nhận được là một số nguyên thì kết quả đúng với công thức.

CH 2

Quan sát hình ảnh mặt nước thu được trên màn khi thay đổi tần số dao động của một quả cầu thì không còn thấy các dao động cực đại và cực tiểu nằm trên các đường xác định nữa. Vậy điều kiện để quan sát được hệ vân giao thoa là gì?

Phương pháp giải:

Từ sự thay đổi của điều kiện so với ban đầu rút ra kết luận.

Lời giải chi tiết:

Điều kiện để quan sát được hệ vân giao thoa là hai quả cầu tạo dao động (nguồn sóng) có cùng tần số dao động, hay hai nguồn sóng là hai nguồn kếp hợp.

CH

Trong một thí nghiệm giao thoa ánh sáng với khe Young, người ta đo dược khoảng cách từ vân trung tâm đến vân sáng thứ mười là 4,0 mm. Ở vị trí cách vân trung tâm 1,0 mm sẽ là vân sáng hay tối?

Phương pháp giải:

Khoảng cách từ vân sáng thứ k đến vân sáng trung tâm là \({x_s} = ki\). Khoảng cách từ vân tối thứ k đến vân sáng trung tâm là \({x_t} = \left( {k - \frac{1}{2}} \right)i\). Tính được i từ \({x_{s10}} = 4,0\)mm. Xác định vị trí 1,0 mm tương ứng với vân sáng hay vân tối.

Lời giải chi tiết:

Khoảng cách vân sáng thứ 10 đến vân sáng trung tâm là: \({x_{s10}} = ki = 10i\). Do đó, khoảng vân là \(i = \frac{{{x_{s10}}}}{{10}} = \frac{{4,0}}{{10}} = 0,4\)(mm).

Ở vị trí cách vân trung tâm \(x = 1,0\)mm, ta có \(\frac{x}{i} = \frac{{1,0}}{{0,4}} = 2,5 = 3 - \frac{1}{2} \Rightarrow x = \left( {3 - \frac{1}{2}} \right)i\). Vậy ở vị trí này là vân tối số 3.

CH 1

Nêu phương án xác định bước sóng ánh sáng bằng thí nghiệm giao thoa với khe Young.

Phương pháp giải:

Khoảng vân phụ thuộc vào bước sóng của ánh sáng giao thoa theo công thức \(i = \frac{{\lambda D}}{a}\). Xác định i, a và D để tìm \(\lambda \).

Lời giải chi tiết:

Đo khoảng cách a giữa khoảng cách giữa hai khe S₁, S₂ và khoảng cách D từ trung điểm hai nguồn sáng đến màn.

Xác định khoảng vân i bằng cách đo khoảng cách \({x_s} = ki\)(đủ lớn để đo) từ vân sáng thứ k đến vân trung tâm. Tính \(i = \frac{{{x_s}}}{k}\).

Khoảng vân phụ thuộc vào bước sóng của ánh sáng giao thoa theo công thức \(i = \frac{{\lambda D}}{a}\). Do đó, bước sóng của ánh sáng giao thoa là \(\lambda  = \frac{{ia}}{D}\).

CH 2

Trong giao thoa ánh sáng trắng, ngoài vân trung tâm có màu trắng, còn có các vân sáng màu trắng khác do có sự chồng lấn các quang phổ bậc khác nhau. Hãy tìm hiểu để nêu cách xác định vị trí của vân sáng màu trắng gần vân trung tâm nhất.

Phương pháp giải:

Khoảng vân \(i = \frac{{\lambda D}}{a}\). Khoảng cách từ vân sáng thứ k đến vân sáng trung tâm là \({x_s} = ki\). Quang phổ bậc k là dải màu liên tục từ vạch sáng tím thứ k đến vạch sáng đỏ thứ k từ vân trung tâm. Vân sáng màu trắng khác xuất hiện do sự chồng lấn các quang phổ bậc khác nhau.

Lời giải chi tiết:

Vị trí có vân sáng màu trắng là vị trí có các vân sáng của các bức xạ có bước sóng khác nhau. Để có vân sáng màu trắng, cần có vân sáng của bức xạ màu đỏ, lục, lam thích hợp lần lượt có bước sóng \({\lambda _r}\), \({\lambda _b}\), \({\lambda _g}\)\(\left( {{\lambda _r} \ge {\lambda _b} \ge {\lambda _g}} \right)\).

Khi đó, tại vị trí có khoảng cách x so với vân trung tâm có vân sáng trắng khi: \(x = {k_1}{i_r} = {k_2}{i_b} = {k_3}{i_g}\) (với k₁, k₂, k₃ là số nguyên).

\( \Rightarrow {k_1}\frac{{{\lambda _r}D}}{a} = {k_2}\frac{{{\lambda _b}D}}{a} = {k_3}\frac{{{\lambda _g}D}}{a}\).

\( \Rightarrow {k_1}{\lambda _r} = {k_2}{\lambda _b} = {k_3}{\lambda _g}\).

Tìm các giá trị k₁, k₂, k₃ nhỏ nhất có thể để xác định vị trí của vân sáng màu trắng gần vân trung tâm nhất.

Lí thuyết