Bài 1. Mô tả sóng trang 36, 37, 38, 39, 40, 41, 42 Vật Lí 11 Cánh diều

KĐ

Ở bờ biển, ta thấy các con sóng nối tiếp nhau xô vào bờ. Các con sóng lớn có thể lan truyền hàng trăm kilômét trên mặt biển trước khi đập vào bờ.

Hình 1.1 mô tả các con sóng đến gần bờ sau quãng đường dài lan truyền trên mặt biển.

Vậy sóng được tạo ra và lan truyền như thế nào?

Phương pháp giải:

Dựa vào hiểu biết về sóng, sự lan truyền sóng để giải thích.

Lời giải chi tiết:

Sóng được tạo ra và lan truyền trong môi trường do nguồn dao động từ bên ngoài tác dụng lên môi trường và do có lực liên kết giữa các phần tử của môi trường.

CH 1

Lấy một ví dụ về sóng

Phương pháp giải:

Dựa vào hiểu biết về sóng trong thực tế nêu ra ví dụ

Lời giải chi tiết:

Sóng âm truyền qua các môi trường rắn, lỏng, khí. Nguồn phát ra âm rồi lan truyền dao động qua các phần tử trong môi trường

CH 2

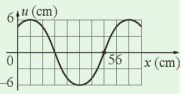
Xác định biên độ và bước sóng được mô tả trong đồ thị li độ u (cm) – khoảng cách x (cm) ở Hình 1.3

Phương pháp giải:

Quan sát đồ thị, sử dụng định nghĩa về biên độ sóng, bước sóng để rút ra các đại lượng này từ đồ thị đã cho.

Lời giải chi tiết:

Biên độ sóng là độ dịch chuyển lớn nhất khỏi vị trí cân bằng của một điểm sóng. Từ đồ thị ta thấy: biên độ sóng \(A = 6\)cm.

Bước sóng là quãng đường mà sóng truyền đi được trong một chu kì sóng.

Ta thấy từ đồ thị, bước sóng \(\lambda \)là khoảng cách giữa hai điểm liên tiếp có li độ bằng biên độ sóng\(\lambda  = 64\)(cm)

CH 1

Chứng tỏ rằng từ định nghĩa về bước sóng, tốc độ sóng, tần số sóng, có thể rút ra công thức (1.2).

Công thức (1.2): \(v = \lambda f\)

Phương pháp giải:

Sử dụng định nghĩa về bước sóng, tốc độ sóng, tần số sóng để suy ra cách tính tốc độ sóng.

Lời giải chi tiết:

Bước sóng \(\lambda \)là quãng đường mà sóng truyền đi được trong một chu kì sóng T.

Tốc độ của sóng v là tốc độ lan truyền của sóng trong không gian.

Do đó: \(v = \frac{\lambda }{T}\)(1).

Tần số sóng f là số dao động mà mỗi điểm sóng thực hiện trong một đơn vị thời gian.

\(f = \frac{1}{T}\)(2).

Từ (1)(2) suy ra \(v = \lambda f\)(đpcm).

CH 2

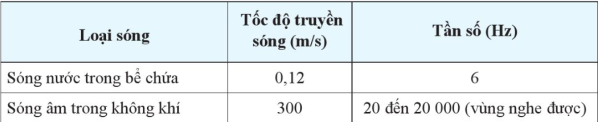
Xác định bước sóng của các sóng ở Bảng 1.1. cho rằng tốc độ sóng trong mỗi môi trường là hằng số với một nhiệt độ và áp suất xác định.

Bảng 1.1. Tốc độ (v) và tần số (f) của một số sóng

Phương pháp giải:

Áp dụng công thức \(v = \lambda f\)suy ra bước sóng \(\lambda \).

Lời giải chi tiết:

Bước sóng của sóng là \(\lambda \), tốc độ sóng là v và tần số sóng là f.

\(v = \lambda f \Rightarrow \lambda  = \frac{v}{f}\)

Sóng nước trong bể chứa có bước sóng là: \(\lambda  = \frac{v}{f} = \frac{{0,12}}{6} = 0,02\)(m).

Sóng âm trong không khí: \(20 \le f \le 20000 \Rightarrow \frac{{300}}{{20}} \ge \frac{v}{f} \ge \frac{{300}}{{20000}} \Rightarrow 0,015 \le \lambda  \le 15\)(m).

CH 1

Lấy ví dụ chứng tỏ sóng truyền năng lượng

Phương pháp giải:

Dựa vào hiểu biết về các hiện tượng truyền sóng chứng minh sóng truyền năng lượng.

Lời giải chi tiết:

Một sợi dây có một đầu được nguồn dao động tác dụng lan truyền sóng trên dây. Khi đó, các phần tử trên dây chỉ dao động tại chỗ, không chuyển động theo sóng. Điều đó chứng tỏ sóng chỉ truyền năng lượng mà không kéo hay đẩy các phần tử trên dây theo.

CH 2

Cường độ của một sóng sẽ bị suy giảm khi truyền đi trong không gian. Khi sóng lan truyền, biên độ sóng giảm dần. Biết rằng cường độ sóng tỉ lệ với bình phương của biên độ sóng. Tại vị trí mà biên độ sóng giảm còn một nửa so với nguồn phát thì cường độ sóng tại đó thay đổi như thế nào so với tại nguồn?

Phương pháp giải:

Dựa vào mối liên hệ của cường độ sóng với biên độ sóng để nhận xét sự thay đổi.

Lời giải chi tiết:

Cường độ sóng I tỉ lệ với bình phương của biên độ sóng A.

\(I = k{A^2}\)(với k là hằng số).

Tại vị trí mà biên độ sóng giảm còn một nửa, cường độ sóng là \(I' = k{\left( {\frac{A}{2}} \right)^2} = \frac{1}{4}k{A^2} = \frac{I}{4}\).

Vậy cường độ sóng giảm đi 4 lần tại vị trí mà biên độ sóng giảm còn một nửa.

CH 1

Mô tả chuyển động của phân tử số 0 trên Hình 1.4 trong thời gian từ \(t = 0\) đến \(t = T\).

Từ đó chỉ ra mối liên hệ giữa khoảng thời gian T biểu diễn trong Hình 1.4 với chu kì dao động của phần tử số 0 và với chu kì sóng trên dây

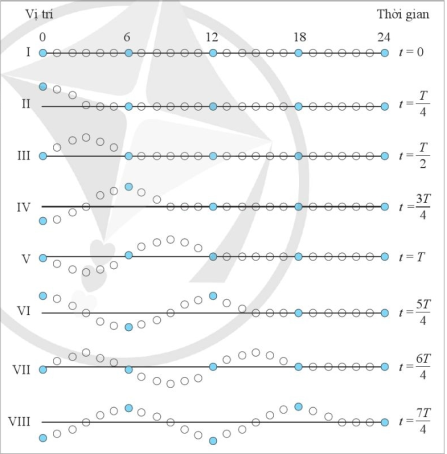
Hình 1.4. Mô hình biểu diễn vị trí các phần tử của sợi dây ở những thời điểm liên tiếp

Phương pháp giải:

Quan sát mô hình và mô tả sự thay đổi vị trí của phần tử số 0 và rút ra kết luận

Lời giải chi tiết:

Tại thời điểm \(t = 0\), phần tử số 0 ở tại ví trí cân bằng, sau đó phần tử chuyển động đến vị trí biên dương tại thời điểm \(t = \frac{T}{4}\)và quay lại vị trí cân bằng tại thời điểm \(t = \frac{T}{2}\). Phần tử tiếp tục đến vị trí biên âm tại thời điểm \(t = \frac{{3T}}{4}\)và quay lại vị trí cân bằng tại thời điểm \(t = T\). Phần tử số 0 hoàn thành một dao động.

Qua đồ thị, ta thấy được T là chu kì sóng trên dây. Mặt khác, T cũng là chu kì dao động của phần tử số 0.

CH 2

Hãy chỉ ra hướng chuyển động của phần tử số 6 ở thời điểm \(\frac{T}{4}\), phần tử số 12 ở thời điểm \(\frac{{5T}}{4}\), phần tử số 18 ở thời điểm \(\frac{{6T}}{4}\) và so sánh với hướng truyền sóng. Từ đó, phân biệt tốc độ của phần tử môi trường đang dao động với tốc độ sóng.

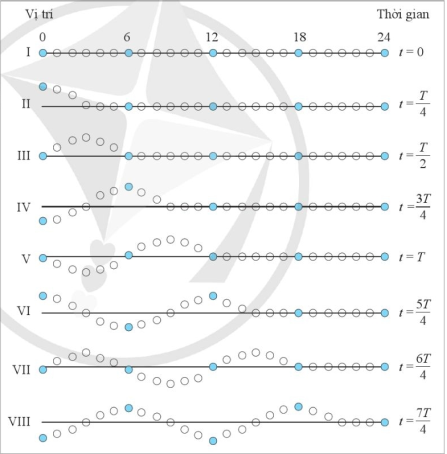
Hình 1.4. Mô hình biểu diễn vị trí các phần tử của sợi dây ở những thời điểm liên tiếp

Phương pháp giải:

Quan sát đồ thị, mô tả hướng chuyển động của các phần tử tại các thời điểm. Rút ra kết luận về sự khác nhau của tốc độ của phần tử môi trường đang dao động với tốc độ sóng.

Lời giải chi tiết:

Ở thời điểm \(t = \frac{T}{4}\), phần tử số 6 đang đứng yên.

Ở thời điểm \(t = \frac{{5T}}{4}\), phần tử số 12 đang ở vị trí biên âm, đang chuyển động hướng lên, về vị trí cân bằng.

Ở thời điểm \(t = \frac{{6T}}{4}\), phần tử số 18 đang ở vị trí cân bằng, đang chuyển động hướng xuống đến vị trí biên âm.

Tốc độ của phần tử môi trường đang dao động là tốc độ dao động của mỗi phần tử, phụ thuộc vào biên độ dao động và tần số dao động, khác với tốc độ lan truyền sóng chỉ phụ thuộc vào môi trường truyền sóng.

CH

Hãy giải thích vì sao về đêm và sáng sớm, ta có thể nghe rõ tiếng chuông chùa hoặc chuông nhà thờ từ rất xa

Phương pháp giải:

Dựa vào sự truyền âm thanh tròn môi trường không khí có nhiệt độ không đồng đều để giải thích hiện tượng

Lời giải chi tiết:

Vào ban đêm và sáng sớm, nhiệt độ không khí ở gần mặt đất thấp hơn so với ở trên cao. Sau khi tiếng chuông truyền đi, sóng âm sẽ truyền lệch về nơi có nhiệt độ thấp hơn (gần mặt đất), vì vậy có thể nghe rõ tiếng chuông từ nơi rất xa.

CH

Bạn sẽ nghe được âm thanh bổng hơn hay trầm hơn của còi xe dẫn đường khi xe đó chạy lại gần bạn?

Phương pháp giải:

Dựa vào kiến thức về hiệu ứng Doppler và mối liên hệ giữa đặc điểm vật lí với đặc điểm sinh lí để xác định.

Lời giải chi tiết:

Khi xe chạy tới gần người, tần số sóng mà người thu được sẽ lớn hơn tần số âm do còi xe phát ra. Âm có tần số càng lớn thì nghe càng cao, nên âm thanh nghe được trong trường hợp này sẽ bổng hơn. 

Lí thuyết