Bài 1. Dao động điều hòa trang 6, 7, 8 Vật Lí 11 Kết nối tri thức

KĐ

Trong cuộc sống hằng ngày và trong kĩ thuật ta thường gặp những vật dao động, ví dụ như dây đàn ghi ta rung động, chiếc đu đung đưa, pít-tông chuyển động lên xuống trong xi lanh của động cơ,... Chuyển động của những vật này được gọi là dao động cơ. Vậy dao động cơ có những đặc điểm gì chung?

Phương pháp giải:

Quan sát hình vẽ và dựa trên sự hiểu biết của bản thân về các sự vật, hiện tượng.

Lời giải chi tiết:

- Chuyển động của dây đàn, xích đu và pít-tông trong xi lanh có đặc điểm chung đều là những chuyển động xung quanh một vị trí cố định.

HĐ

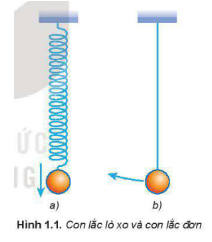
Treo một vật nhỏ, nặng vào đầu tự do của một lò xo nhẹ (Hình 1.1a) hoặc một dây nhẹ không dãn ta có con lắc lò xo hoặc con lắc đơn (Hình 1.1b).

1. Xác định vị trí cân bằng của vật.

2. Kéo vật lệch khỏi vị trí cân bằng rồi thả ra cho chuyển động. Quan sát chuyển động của mỗi vật và cho nhận xét về đặc điểm chung của chúng.

Phương pháp giải:

Quan sát thí nghiệm để trả lời.

Lời giải chi tiết:

1. Vị trí cân bằng của con lắc đơn trong thí nghiệm trên là vị trí mà và dây treo có phương thẳng đứng, vị trí cân bằng của con lắc lò xo là vị trí mà ở đó lò xo không co không dãn.

2. Kéo vật lệch khỏi vị trí cân bằng rồi thả ra cho chuyển động thì:

+ Con lắc lò xo dao động lên – xuống theo phương thẳng đứng.

+ Con lắc đơn dao động qua lại theo một cung tròn xung quanh vị trí cân bằng.

CH

Nêu những ví dụ về dao động cơ mà em biết.

Phương pháp giải:

Dao động là những chuyển động qua lại xung quanh vị trí cân bằng.

Lời giải chi tiết:

Một số ví dụ về dao động cơ: 

+ Dao động qua lại của con lắc trong đồng hồ quả lắc.

+ Chuyển động của xích đu hoặc chiếc bập bênh.

CH

Một vật dao động điều hoà có phương trình \({\rm{x}} = 2\cos \left( {4\pi {\rm{t}} + \frac{\pi }{2}} \right)({\rm{cm}})\)

Hãy xác định:

a) Biên độ và pha ban đầu của dao động.

b) Pha và li độ của dao động khi \(t = 2\left( s \right)\)

Phương pháp giải:

Vận dụng kiến thức đã học về các đại lượng của phương trình dao động điều hoà.

Phương trình dao động điều hoà có dạng: \(x = A\cos \left( {\omega t + \varphi } \right)\) với:

+ \(x\) là li độ dao động.

+ \(A\) là biên độ dao động.

+ \(\omega \) là tần số góc của dao động.

+ \(\left( {\omega {\rm{t}} + \varphi } \right)\) là pha của dao động ở thời điểm \(t\).

+ \(\varphi \) là pha ban đầu.

Lời giải chi tiết:

a. Từ phương trình \({\rm{x}} = 2\cos \left( {4\pi {\rm{t}} + \frac{\pi }{2}} \right)({\rm{cm}})\) ta có:

+ Biên độ: \(A = 2\)cm.

+ Pha ban đầu \(\varphi  = \frac{\pi }{2}\) rad.

b. Thay \(t = 2\left( s \right)\) vào phương trình dao động ta được:

+ Pha của dao động là: \(4\pi .2 + \frac{\pi }{2} = 8,5\pi \).

+ Li độ dao động là: \(x = 2\cos \left( {4\pi .2 + \frac{\pi }{2}} \right) = 0\).

HĐ

Đồ thị li độ - thời gian của một con lắc đơn dao động điều hoà được mô tả trên Hình 1.3.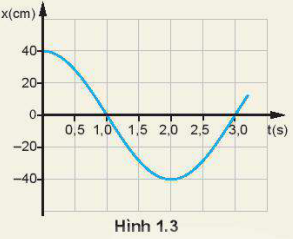

1. Hãy mô tả dao động điều hoà của con lắc đơn.

2. Xác định biên độ và li độ của con lắc ở các thời điểm \(t = 0,{\rm{ }}t = 0,5\;s,{\rm{ }}t = 2,0\;s\).

Phương pháp giải:

1. Vận dụng kiến thức đã học trong phần 1. Đồ thị dao động điều hoà.

2. Để tìm li độ tại thời điểm \(t\) ta thay \(t\) vào phương trình dao động hoặc quan sát đồ thị.

Lời giải chi tiết:

1. Từ đồ thị ta thấy:

- Biên độ dao động là giá trị lớn nhất của li độ: \(A = {x_{\max }} = 40\left( {cm} \right)\)

- Từ vị trí cao nhất đến vị trí thấp nhất gần mất thời gian là một nửa chu kì nên ta có: \(\frac{T}{2} = 2\left( s \right) \Rightarrow T = 4\left( s \right)\)

Tần số góc của con lắc là: \(\omega  = \frac{{2\pi }}{T} = \frac{{2\pi }}{4} = \frac{\pi }{2}\) (rad)

- Lúc \(t = 0\), con lắc đang ở vị trí biên dương: \(x = A = 40cm.\)

\( \Rightarrow x = A\cos \varphi  \Leftrightarrow \cos \varphi  = \frac{x}{A} = 1 \Rightarrow \varphi  = 0\)

Vậy phương trình dao động: \(x = 40\cos \left( {\frac{\pi }{2}t} \right)\) cm.

2.

- Lúc \(t = 0\), con lắc đang ở vị trí biên dương: \(x = A = 40cm.\)

- Lúc \(t = 0,5s,\)li độ của con lắc là: \(x = 40\cos \left( {\frac{\pi }{2}.0,5} \right) = 40.\cos \frac{\pi }{4} = 20\sqrt 2 \left( {cm} \right)\)

- Lúc \(t = 1\left( s \right)\), quan sát trên đồ thị li độ con lắc là: \(x = 0\).

- Lúc \(t = 2\left( s \right)\), li độ của con lắc là \(x =  - A =  - 40\left( {cm} \right)\).

CH

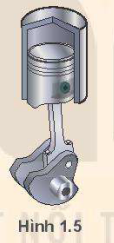
Pít-tông của một động cơ đốt trong dao động trên một đoạn thẳng dài \(16\;cm\) và làm cho trục khuỷu của động cơ quay đều (Hình 1.5). Xác định biên độ dao động của một điểm trên mặt pít-tông.

Phương pháp giải:

Khi vật dao động với biên độ \(A\) thì quỹ đạo của vật là một đoạn thẳng có độ dài \(2A.\)

Lời giải chi tiết:

Nếu coi khoảng cách từ pitông đến hình chiếu của khuỷu lên trục xilanh gần đúng bằng độ dài của biên, tức là không đổi, thì pitông dao động gần đúng như hình chiếu của khuỷu lên trục xilanh.

Biên độ dao động của một điểm trên mặt pít-tông là: \(A = \frac{{16}}{2} = 8\left( {cm} \right)\).

Lí thuyết