Bài tập cuối chương IV trang 64, 65, 66, 67 SBT Vật lí 11 Kết nối tri thức với cuộc sống
Số electron dịch chuyển qua tiết diện thẳng của dây trong thời gian 2 s là 6,25. . Khi đó dòng điện qua dây dẫn có cường độ là
IV.1
Số electron dịch chuyển qua tiết diện thẳng của dây trong thời gian 2 s là 6,25.\({10^{18}}\). Khi đó dòng điện qua dây dẫn có cường độ là
A. 1A
B. 2A.
C. 1,25A.
D. 0,5A.
Phương pháp :
Vận dụng biểu thức: \(N = \frac{{It}}{{\left| e \right|}}\)
Lời giải chi tiết :
Dòng điện qua dây dẫn có cường độ là : \(I = \frac{{N\left| e \right|}}{t} = \frac{{6,{{25.10}^{18}}.1,{{6.10}^{ - 19}}}}{2} = 0,5A\)
Đáp án : D
IV.2
Số electron đi qua tiết diện thẳng của một dây dẫn kim loại trong 1 s là
1,25. \({10^{19}}\). Biết rằng dòng điện không đổi, điện lượng đi qua tiết diện đó trong 15 giây là
A. 10C.
B. 20C.
C. 30C.
D. 40C.
Phương pháp :
Vận dụng biểu thức: \(N = \frac{{It}}{{\left| e \right|}}\)
Áp dụng biểu thức xác định điện lượng: \(q = It\)
Lời giải chi tiết :
Dòng điện qua dây dẫn có cường độ là : \(I = \frac{{N\left| e \right|}}{t} = \frac{{1,{{25.10}^{19}}.1,{{6.10}^{ - 19}}}}{1} = 2A\)
Điện lượng đi qua tiết diện đó trong 15 giây là : \(q = It = 2.15 = 30C\)
Đáp án : C
IV.3
Cường độ dòng điện chạy qua tiết diện thẳng của dây dẫn là 1,5 A. Trong khoảng thời gian 3 s thì điện lượng chuyển qua tiết diện dây là
A. 0,5C.
B. 2,0C.
C. 4,5C.
D. 5,4C.
Phương pháp :
Áp dụng biểu thức xác định điện lượng: \(q = It\)
Lời giải chi tiết :
Trong khoảng thời gian 3 s thì điện lượng chuyển qua tiết diện dây là : \(q = It = 1,5.3 = 4,5C\)
Đáp án : C
IV.4
Cho một dòng điện không đổi chạy qua một dây dẫn, trong 10 s, điện lượng chuyển qua tiết diện thẳng của dây dẫn là 2 C. Sau 60 s điện lượng chuyển qua tiết diện thẳng đó là
A. 6C.
B. 12C.
C. 60C.
D. 20C.
Phương pháp :
Áp dụng biểu thức xác định điện lượng: \(q = It\)
Lời giải chi tiết :
Dòng điện qua dây dẫn có cường độ là : \(I = \frac{q}{t} = \frac{2}{{10}} = 0,2A\)
Sau 60 s điện lượng chuyển qua tiết diện thẳng đó là : \(q = It = 0,2.60 = 12C\)
Đáp án : B
IV.5
Cường độ dòng điện chạy qua điện trở R = 5 \(\Omega \) là 0,5 A. Hiệu điện thế giữa hai đầu điện trở là
A. 2,5V.
B. 25V.
C. 0,5V.
D. 10V.
Phương pháp :
Định luật Ohm : \(I = \frac{U}{R}\)
Lời giải chi tiết :
Hiệu điện thế giữa hai đầu điện trở là : \(U = I.R = 5.0,5 = 2,5V\)
Đáp án : A
IV.6
Đặt một hiệu điện thế U = 12V vào hai đầu một điện trở, cường độ dòng điện chạy qua điện trở là 2 A. Nếu tăng hiệu điện thế lên hai lần thì cường độ dòng điện có giá trị
A. 4A.
B. 2A.
C. 12A.
D. 0,24A.
Phương pháp :
Định luật Ohm : \(I = \frac{U}{R}\)
Lời giải chi tiết :
Giá trị điện trở : \(R = \frac{U}{I} = \frac{{12}}{2} = 6\Omega \)
Nếu tăng hiệu điện thế lên hai lần thì cường độ dòng điện có giá trị là :
\({I^'} = \frac{{{U^'}}}{R} = \frac{{2U}}{R} = \frac{{24}}{6} = 4A\)
Đáp án : A
IV.7
Đặt vào hai đầu một điện trở R một hiệu điện thế U = 12 V, cường độ dòng điện chạy qua điện trở là 1,5 A. Nếu giữ nguyên hiệu điện thế nhưng muốn cường độ dòng điện chạy qua điện trở là giảm đi 0,5 A thì ta phải tăng giá trị điện trở thêm một lượng là
A. 5,0 \(\Omega \)
B. 4,5 \(\Omega \)
C. 4,0 \(\Omega \)
D. 5,5 \(\Omega \)
Phương pháp :
Định luật Ohm : \(I = \frac{U}{R}\)
Lời giải chi tiết :
Giá trị điện trở ban đầu là : \(R = \frac{U}{I} = \frac{{12}}{{1,5}} = 8\Omega \)
Giữ nguyên hiệu điện thế nhưng muốn cường độ dòng điện chạy qua điện trở là giảm đi 0,5 A thì giá trị điện trở : \({R^'} = \frac{U}{{{I^'}}} = \frac{{12}}{{I - 0,5}} = \frac{{12}}{{1,5 - 0,5}} = 12\Omega \)
=> ta phải tăng giá trị điện trở thêm một lượng là : \(\Delta R = {R^'} - R = 12 - 8 = 4\Omega \)
Đáp án : C
IV.8
Khi đặt hiệu điện thế U = 8 V vào hai đầu một dây dẫn thì dòng điện chạy qua dây có cường độ Ì = 0,2A. Nếu tăng hiệu điện thế thêm 4 V thì dòng điện chạy qua dây dẫn khi đó có cường độ là
A. 0,2A.
B. 0,3A.
C. 0,4A.
D. 0,8A.
Phương pháp :
Định luật Ohm : \(I = \frac{U}{R}\)
Lời giải chi tiết :
Giá trị điện trở ban đầu là : \(R = \frac{U}{I} = \frac{8}{{0,2}} = 40\Omega \)
Nếu tăng hiệu điện thế thêm 4 V thì dòng điện chạy qua dây dẫn khi đó có cường độ là : \({I^'} = \frac{{{U^'}}}{R} = \frac{{8 + 4}}{{40}} = 0,3A\)
Đáp án : A
IV.9
Công của lực lạ làm di chuyển điện tích 4 C từ cực âm đến cực dương bên trong nguồn điện là 24 J. Suất điện động của nguồn là
A. 0,16V.
B. 6V.
C. 96V.
D. 0,6V.
Phương pháp :
Công thức tính suất điện động của nguồn : \(\xi = \frac{A}{q}\)
Lời giải chi tiết :
Suất điện động của nguồn là : \(\xi = \frac{A}{q} = \frac{{24}}{4} = 6V\)
Đáp án : B
IV.10
Suất điện động của một nguồn điện là 1,5 V, lực lạ làm di chuyển điện tích thực hiện một công 6 mJ. Lượng điện tích dịch chuyển khi đó là
A. 15. \({10^{ - 3}}\)C.
B. 4. \({10^{ - 3}}\)C.
C. 0,5. \({10^{ - 3}}\)C.
D. 1,5.\({10^{ - 3}}\)C.
Phương pháp :
Công thức tính suất điện động của nguồn : \(\xi = \frac{A}{q}\)
Lời giải chi tiết :
Lượng điện tích dịch chuyển khi đó là : \(q = \frac{A}{\xi } = \frac{{{{6.10}^{ - 3}}}}{{1,5}} = {4.10^{ - 3}}C\)
Đáp án : B
IV.11
Một nguồn điện có suất điện động 24 V. Để chuyển một điện lượng 10 C qua nguồn thì lực lạ phải sinh một công là
A.100 J
B. 2,4 J
C. 24 J
D. 240 J
Phương pháp :
Công thức tính suất điện động của nguồn : \(\xi = \frac{A}{q}\)
Lời giải chi tiết :
Để chuyển một điện lượng 10 C qua nguồn thì lực lạ phải sinh một công là
\(A = q\xi = 10.24 = 240J\)
Đáp án : D
IV.12
Một nguồn điện có suất điện động không đổi, để chuyển một điện lượng 5 C thì lực lạ phải sinh một công là 20 mJ. Để chuyển một điện lượng 10 C qua nguồn thì lực lạ phải sinh một công là
A.10 mJ
B. 15 mJ
C. 20 mJ
D. 40 mJ
Phương pháp :
Công thức tính suất điện động của nguồn : \(\xi = \frac{A}{q}\)
Lời giải chi tiết :
Suất điện động của nguồn là : \(\xi = \frac{A}{q} = \frac{{{{20.10}^{ - 3}}}}{5} = {4.10^{ - 3}}V\)
Để chuyển một điện lượng 10 C qua nguồn thì lực lạ phải sinh một công là
\(A = q\xi = {10.4.10^{ - 3}} = 40mJ\)
Đáp án : D
IV.13
Một acquy có ghi thông số 12 V - 20 Ah. Thông số này cho biết
A. điện lượng cực đại của acquy là 7 200 C.
B. điện trở trong của acquy là 0,16 O.
C. dòng điện lớn nhất mà acquy có thể cung cấp là 20 A.
D. năng lượng dự trữ của acquy là 12.\({10^6}\)J
Phương pháp :
Vận dụng kiến thức nguồn điện.
Lời giải chi tiết :
Thông số này cho biết điện lượng cực đại của acquy là
20 Ah = 20.3600 =72 000 C
Đáp án :
IV.14
Công suất điện cho biết
A. khả năng thực hiện công của dòng điện.
B. năng lượng của dòng điện.
C. lượng điện năng sử dụng trong một đơn vị thời gian.
D. mức độ mạnh - yếu của dòng điện.
Phương pháp :
Vận dụng kiến thức nguồn điện , công suất điện .
Lời giải chi tiết :
Công suất điện cho biết lượng điện năng sử dụng trong một đơn vị thời gian.
Đáp án : C
IV.15
Trên các thiết bị điện gia dụng thường có ghi 220 V và số oát (W). Số oát này có ý nghĩa gì?
A. Công suất tiêu thụ điện của dụng cụ khi nó được sử dụng với những hiệu
điện thế nhỏ hơn 220 V.
B. Công suất tiêu thụ điện của dụng cụ khi nó được sử dụng với đúng hiệu
điện thế 220 V.
C. Công mà dòng điện thực hiện trong một phút khi dụng cụ này được sử dụng với đúng hiệu điện thế 220 V.
D. Điện năng mà dụng oụ tiêu thụ trong một giờ khi nó được sử dụng với đúng hiệu điện thế 220 V
Phương pháp :
Vận dụng kiến thức nguồn điện , công suất điện .
Lời giải chi tiết :
Số oát này có ý nghĩa công suất tiêu thụ điện của dụng cụ khi nó được sử dụng với đúng hiệu điện thế 220 V
Đáp án : B
IV.16
Công suất định mức của các dụng cụ điện là
A. công suất lớn nhất mà dụng cụ đó có thể đạt được.
B. công suất tối thiểu mà dụng cụ đó có thể đạt được.
C. công suất đạt được khi nó hoạt động bình thường.
D. công suất trung bình của dụng cụ đó.
Phương pháp :
Vận dụng kiến thức nguồn điện , công suất điện .
Lời giải chi tiết :
Công suất định mức của các dụng cụ điện là công suất đạt được khi nó hoạt động bình thường.
Đáp án :C
IV.17
Tính tốc độ dịch chuyển có hướng của electron trong một dây đồng tiết
diện thẳng 1 \(m{m^2}\) có dòng điện 1 A chạy qua. Cho biết khối lượng riêng của
đồng \(\rho = {9.10^3}kg/{m^3}\)và mỗi nguyên tử đồng cho một electron tự do.
Phương pháp :
Công thức liên hệ giữa m , D là \(m = D.V\)
Một mol nguyên tử Cu có chứa \(6,{023.10^{23}}\)nguyên tử Cu
Khối lượng mol nguyên tử của đồng là : \({64.10^{ - 3}}kg/mol\)
Cường độ dòng điện chạy qua một dây dẫn kim loại : \(I = Snve\)
Lời giải chi tiết :
Ta xét 1mol đồng: Vì mỗi nguyên tử đồng đóng góp một êlectron dẫn nên số electron tự do trong 1 mol đồng là: \({N_e} = {N_A} = 6,{023.10^{23}}\)hạt.
Khối lượng mol nguyên tử của đồng là : \({64.10^{ - 3}}kg/mol\)
Thể tích của 1 mol đồng là : \(V = \frac{m}{D} = \frac{{{{64.10}^{ - 3}}}}{{{{9.10}^3}}} = 7,{1.10^{ - 6}}\left( {{m^3}/mol} \right)\)
Mật độ e tự do trong dây đồng là : \(n = \frac{{{N_e}}}{V} = \frac{{6,{{023.10}^{23}}}}{{7,{{1.10}^{ - 6}}}} = 8,{48.10^{28}}\left( {{m^{ - 3}}} \right)\)
=> Tốc độ dịch chuyển có hướng của electron trong một dây đồng tiết
diện thẳng 1 \(m{m^2}\) có dòng điện 1 A chạy qua là : \(v = \frac{I}{{nSe}} = \frac{1}{{8,{{48.10}^{28}}{{.1.10}^{ - 3}}.1,{{6.10}^{ - 19}}}} = 7,{3.10^{ - 5}}m/s = 0,073mm/s\)
IV.18
Bạc có khối lượng riêng 10,5 \(g/c{m^3}\)và mỗi nguyên tử cho một electron tự do. Dây bạc hình trụ có đường kính bằng bao nhiêu nếu dòng điện chạy trong dây bạc có cường độ I = 1 A, tốc độ dịch chuyển có hướng của các electron tự do là 3,4.\({10^{ - 5}}\)m/s.
Phương pháp :
Công thức liên hệ giữa m , D là \(m = D.V\)
Một mol nguyên tử bạc có chứa \(6,{023.10^{23}}\)nguyên tử Cu
Khối lượng mol nguyên tử của bạc là : \(108g/mol\)
Cường độ dòng điện chạy qua một dây dẫn kim loại : \(I = Snve\)
Diện tích hình tròn : \(S = \pi {\left( {\frac{d}{2}} \right)^2}\)
Lời giải chi tiết :
Ta xét 1mol bạc: Vì mỗi nguyên tử bạc đóng góp một êlectron dẫn nên số electron tự do trong 1 mol bạc là: \({N_e} = {N_A} = 6,{023.10^{23}}\)hạt.
Khối lượng mol nguyên tử của bạc là : \(108g/mol\)
Thể tích của 1 mol bạc là : \(V = \frac{m}{D}\)
=> Mật độ e tự do trong dây bạc là : \(n = \frac{{{N_e}}}{V} = \frac{{{N_e}.D}}{m} = \frac{{6,{{023.10}^{23}}}}{{108}}.10,{5.10^6} = 5,{86.10^{28}}\left( {e/{m^3}} \right)\)
=> diện tích tiết diện của dây hình trụ nếu dòng điện chạy trong dây bạc có cường độ I = 1 A, tốc độ dịch chuyển có hướng của các electron tự do là 3,4.\({10^{ - 5}}\)m/s là : \(S = \frac{I}{{nve}} = \frac{1}{{5,{{86.10}^{28}}.3,{{4.10}^{ - 5}}.1,{{6.10}^{ - 19}}}} = {3.10^{ - 6}}\left( {{m^2}} \right)\)
Ta có diện tích hình tròn : \(S = \pi {\left( {\frac{d}{2}} \right)^2}\)=> đường kính của dây bạc là \(d = 2\sqrt {\frac{S}{\pi }} = 2\sqrt {\frac{{{{3.10}^{ - 6}}}}{\pi }} = 0,002m = 2mm\)
IV.19
Cho mạch điện như Hình IV.1. Biết giá trị cáo điện trở:\({R_1} = 4\Omega \), \({R_2} = 6\Omega \), \({R_3} = 12\Omega \). Hiệu điện thế giữa hai đầu đoạn mạch \({U_{AD}}\)= 6V. Giả sử điện trở của dây nối và của ampe kế không đáng kể. Tính số chỉ của ampe kế khi:
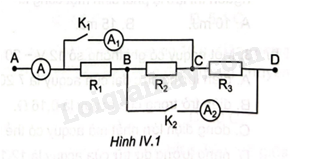
a)\({K_1}\) ngắt, \({K_2}\)đóng.
b) \({K_1}\)đóng, \({K_2}\) ngắt.
c) \({K_1}\),\({K_2}\)đều ngắt,
d) \({K_1}\), \({K_2}\) đều đóng.
Phương pháp :
Định luật Ohm trong các đoạn mạch.
Lời giải chi tiết :
a)\({K_1}\) ngắt, \({K_2}\)đóng.
B với D nối với nhau bằng dây nối => chập B lại với điểm D dòng ưu tiên qua dây nối không qua \({R_2};{R_3}\)=> có thể bỏ qua \({R_2};{R_3}\)=> mạch chỉ còn \({R_1}\)
=> Số chỉ ampe kế : \(I = \frac{{{U_{AD}}}}{{{R_1}}} = \frac{6}{4} = 1,5A\)
b) \({K_1}\)đóng, \({K_2}\) ngắt.
A với C nối với nhau bằng dây nối => chập A lại với điểm C dòng ưu tiên qua dây nối không qua \({R_1};{R_2}\)=> có thể bỏ qua \({R_1};{R_2}\)=> mạch chỉ còn \({R_3}\)
=> Số chỉ ampe kế : \(I = \frac{{{U_{AD}}}}{{{R_3}}} = \frac{6}{{12}} = 0,5A\)
c) \({K_1}\),\({K_2}\)đều ngắt
Mạch mới
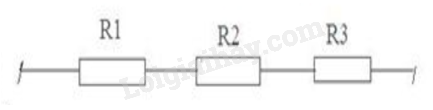
Mạch nối tiếp nên cường độ dòng điện bằng nhau => Số chỉ ampe kế :
\(I = \frac{{{U_{AD}}}}{{{R_N}}} = \frac{{{U_{AD}}}}{{{R_1} + {R_2} + {R_3}}} = \frac{6}{{4 + 6 + 12}} = \frac{3}{{11}}A\)
d) \({K_1}\), \({K_2}\) đều đóng.
Vì ampe kế có điện trở không đáng kể nên:
+ A và C có cùng điện thế → chập C và A lại.
+ B và D có cùng điện thế → chập D và B lại.
Mạch điện được vẽ lại như sau:
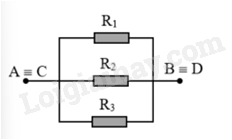
Ta có : \({R_1}//{R_2}//{R_3} = > \frac{1}{{{R_{AB}}}} = \frac{1}{{{R_1}}} + \frac{1}{{{R_2}}} + \frac{1}{{{R_3}}} = \frac{1}{4} + \frac{1}{6} + \frac{1}{{12}} = > {R_{AB}} = 0,5A\)
=> Số chỉ ampe kế \( = > {I_A} = \frac{U}{{{R_{AB}}}} = \frac{6}{{0,5}} = 12A\);
\({I_1} = \frac{U}{{{R_1}}} = \frac{6}{4} = 1,5A\); \({I_3} = \frac{U}{{{R_3}}} = \frac{6}{{12}} = 0,5A\)
=> Số chỉ ampe kế 1 : \({I_A} = {I_1} + {I_{A1}} = > {I_{A1}} = {I_A} - {I_1} = 12 - 1,5 = 10,5A\)
=> Số chỉ ampe kế 2 : \({I_A} = {I_3} + {I_{A2}} = > {I_{A2}} = {I_A} - {I_3} = 12 - 0,5 = 11,5A\)
IV.20
Một dây điện trở có thể làm 500 mL nước tăng nhiệt độ thêm 60° trong 5 phút khi hoạt động ở hiệu điện thế 220 V. Biết nhiệt dung riêng của nước là 4 180 J/kg.K
a) Tính công suất toả nhiệt của điện trở,
b) Cường độ dòng điện qua điện trở là bao nhiêu?
Phương pháp :
Công thức tính nhiệt lượng cần để tăng nhiệt : \(Q = mc\Delta t\)
Lời giải chi tiết :
a) Ta có ; 500ml = 0,5 l = 0,5 kg
Nhiệt lượng cần để tăng nhiệt độ của nước thêm 60° là :
\(Q = mc\Delta t = 0,5.4180.60 = 125400J\)
=> công suất toả nhiệt của điện trở là : \(P = \frac{Q}{t} = \frac{{125400}}{5} = 25080W\)
b) Cường độ dòng điện qua điện trở là : \(I = \frac{P}{U} = \frac{{25080}}{{220}} = 114A\)
IV.21
Hai điện trở \({R_1}\)và \({R_2}\) mắc nối tiếp thì điện trở tương đương lớn gấp 6,25 lần điện trở tương đương khi mắc song song. Tính tỉ số hai điện trở \(\frac{{{R_1}}}{{{R_2}}}\)
Phương pháp :
Định luật Ohm trong các đoạn mạch .
Lời giải chi tiết :
Theo đề bài ta có : \({R_1} + {R_2} = 6,25.\frac{{{R_1}.{R_2}}}{{{R_1} + {R_2}}} = > {\left( {{R_1} + {R_2}} \right)^2} = 4,25{R_1}.{R_2}\)
Đặt \({R_2} = 1 = > R_1^2 - 4,25{R_1} + 1 = 0\) => Giải pt ta được : \({R_1} = 4\)hoặc \({R_1} = 0,25\)
=> \(\frac{{{R_1}}}{{{R_2}}} = 4\) hoặc \(\frac{{{R_1}}}{{{R_2}}} = 0,25\)
IV.22
Cho một nguồn điện có suất điện động \(\xi \) và điện trở trong r. Nguồn điện được mắc với một điện trở R tạo thành mạch kín. Vẽ đồ thị phụ thuộc của hiệu suất nguồn điện vào cường độ dòng điện.
Phương pháp :
Định luật Ohm trong các đoạn mạch .
Lời giải chi tiết :
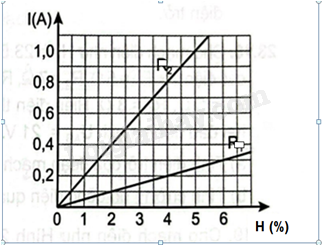
Hiệu suất nguồn điện :\(H = \frac{{{A_{ich}}}}{{{A_{ng}}}} = \frac{{UIt}}{{\xi It}} = \frac{U}{\xi } = \frac{{R.I}}{\xi }\) => đồ thị phụ thuộc của hiệu suất nguồn điện vào cường độ dòng điện là một đường thẳng đi qua gốc tọa độ
Hình minh họa :
IV.23
Một nguồn điện có điện trở trong 0,1 \(\Omega \)được mắc nối tiếp với điện trở R=4,8\(\Omega \) tạo thành mạch kín. Khi đó hiệu điện thế giữa hai cực của nguồn điện là 12 V. Tính suất điện động của nguồn và cường độ dòng điện chạy
trong mạch.
Phương pháp :
Định luật Ohm trong các đoạn mạch .
Công thức tính suất điện động.
Lời giải chi tiết :
Cường độ dòng điện chạy trong mạch là : \(I = \frac{U}{R} = \frac{{12}}{{4,8}} = 2,5A\)
Suất điện động của nguồn điện : \(\xi = U + I.r = 12 + .2,5.0,1 = 12,25V\)
IV.24
Mạch kín gồm nguồn điện có suất điện động \(\xi \)= 24 V, điện trở trong r = 0,5 \(\Omega \) và hai điện trở \({R_1}\)= 10\(\Omega \) ; \({R_2}\)= 50 \(\Omega \) mắc nối tiếp. Một vôn kế mắc
song song với điện trở \({R_2}\)chỉ giá trị 16 V. Tìm điện trở của vôn kế.
Phương pháp :
Định luật Ohm trong các đoạn mạch .
Công thức tính suất điện động.
Lời giải chi tiết :
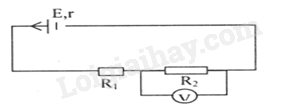
Gọi \({R_v}\)là điện trở của vôn kế , \({R_N}\)là điện trở của mạch ngoài .
Ta có :\(I = \frac{\xi }{{{R_N} + r}} = > I{R_N} + Ir = \xi = > {U_N} = \xi - Ir\left( 1 \right)\)
Mặt khác \({U_N} = {U_1} + {U_2} = I{R_1} + \,{U_2}\left( 2 \right)\)
Từ (1) và (2) ta được : \(I{R_1} + \,{U_2} = \xi - Ir = > I\left( {{R_1} + r} \right) = \xi - {U_2}\)
\( = > I = \frac{{\xi - {U_2}}}{{{R_1} + r}} = \frac{{24 - 16}}{{10 + 0,5}} = 0,76A\)
Mà \(I = {I_1} + {I_2} = > {I_1} = I - {I_2} = I - \frac{{{U_2}}}{{{R_2}}} = > {I_1} = 0,76 - \frac{{16}}{{50}} = 0,44A\)
=> điện trở của vôn kế :\({R_v} = \frac{{{U_v}}}{{{I_1}}} = \frac{{16}}{{0,44}} = 36,36\Omega \)
IV.25
Hai điện trở \({R_1}\) = 2 \(\Omega \), \({R_2}\)= 6 \(\Omega \) mắc vào nguồn điện có suất điện động \(\xi \) và điện trở trong r. Khi \({R_1}\) , \({R_2}\) mắc nối tiếp, cường độ dòng điện trong mạch chính I= 0,5 A. Khi \({R_1}\) , \({R_2}\) mắc song song, cường độ dòng điện trong mạch chính I'= 1,8A. Tìm giá trị của suất điện động \(\xi \) và điện trở trong r.
Phương pháp :
Định luật Ohm trong các đoạn mạch .
Công thức tính suất điện động.
Lời giải chi tiết :
Khi \(\left( {{R_1}nt{R_2}} \right) = > {R_N} = {R_1} + {R_2} = 8\Omega = > {I_N} = \frac{\xi }{{{R_N} + r}} = > \frac{\xi }{{8 + r}} = 0,5\left( 1 \right)\)
Khi \(\left( {{R_1}//{R_2}} \right) = > R_N^' = \frac{{{R_1}.{R_2}}}{{{R_1} + {R_2}}} = 1,5\Omega = > {I_S} = \frac{\xi }{{R_N^' + r}} = > \frac{\xi }{{1,5 + r}} = 1,8\left( 2 \right)\)
Từ (1) và (2) => hệ pt
\(\left\{ {_{2,7 + 1,8r = \xi }^{4 + 0,5r = \xi }} \right.\)
=> \(r = 1\Omega ;\xi = 4,5V\)
IV.26
Hai điện trở \({R_1}\)= 20 \(\Omega \) và điện trở \({R_2}\)chưa biết giá trị được mắc nối tiếp với nhau và mắc vào hiệu điện điện thế U = 220 V thì điện trở \({R_2}\)tiêu thụ một công suất là \({{\rm P}_2}\) = 600 W. Tính giá trị điện trở \({R_2}\)biết rằng dòng điện chạy qua điện trở \({R_2}\)có giá trị không lớn hơn 5 A.
Phương pháp :
Định luật Ohm trong các đoạn mạch .
Công thức tính công suất : \({\rm P} = R{I^2}\)
Lời giải chi tiết :
Ta có : \({{\rm P}_2} = {R_2}I_2^2 = > I_2^2 = \frac{{{{\rm P}_2}}}{{{R_2}}}\) mà ta có \({I_1} = {I_2} = I = > U = {U_1} + {U_2} = {I_1}{R_1} + {I_2}{R_2} = I.\left( {{R_1} + {R_2}} \right) = 220V\)
\( = > I = \frac{{220}}{{\left( {{R_1} + {R_2}} \right)}} = > {I^2} = \frac{{{{220}^2}}}{{{{\left( {{R_1} + {R_2}} \right)}^2}}} = \frac{{{{\rm P}_2}}}{{{R_2}}}\)
\( = > \left\{ {_{{R_2} = \frac{{50}}{3}\Omega }^{{R_2} = 24\Omega }} \right.\)
IV.27
Từ một nguồn điện có hiệu điện thế U, điện năng được truyền qua dây dẫn tới nơi tiêu thụ. Biết điện trở dây dẫn là R = 5 \(\Omega \), công suất của nguồn điện là P = 62 kW. Tìm độ giảm thế trên dây, công suất hao phí và hiệu suất tải điện nếu:
a) U=6200 V.
b) U=620V.
Phương pháp :
Công suất hao phí :\({P_{hp}} = {I^2}.R\)
Hiệu suất tải điện : \(H = 1 - \frac{{{P_{hp}}}}{P}\)
Công thức tính công suất của vật tiêu thụ điện toả nhiệt là : \(P = \frac{{{U^2}}}{R} = U.I = R.{I^2}\)
Lời giải chi tiết :
a) Nguồn điện có hiệu điện thế U=6200 V.
Ta có cường độ dòng điện \(I = \frac{{\rm P}}{U} = \frac{{62000}}{{6200}} = 10A\)
=> Độ giảm thế : \(U = I.R = 10.5 = 50V\)
Công suất hao phí trên đường dây là : \({P_{hp}} = {I^2}.R = \frac{{{P^2}}}{{{U^2}}}.R = {\left( {\frac{{62000}}{{6200}}} \right)^2}.5 = 500W\)
Hiệu suất tải điện : \(H = 1 - \frac{{{P_{hp}}}}{P} = 1 - \frac{{500}}{{62000}} = 99\% \)
b) Nguồn điện có hiệu điện thế U=620 V.
Ta có cường độ dòng điện \(I = \frac{{\rm P}}{U} = \frac{{62000}}{{620}} = 100A\)
=> Độ giảm thế : \(U = I.R = 100.5 = 500V\)
Công suất hao phí trên đường dây là : \({P_{hp}} = {I^2}.R = \frac{{{P^2}}}{{{U^2}}}.R = {\left( {\frac{{62000}}{{620}}} \right)^2}.5 = 50000W\)
Hiệu suất tải điện : \(H = 1 - \frac{{{P_{hp}}}}{P} = 1 - \frac{{50000}}{{62000}} = 19,35\% \)
IV.28
Người ta dùng một ấm nhôm có khối lượng \({m_1}\) = 0,4 kg để đun một lượng nước \({m_2}\) = 2 kg thì sau 20 phút nước sẽ sôi. Bếp điện có hiệu suất H = 60% và được dùng ở mạng điện có hiệu điện thế U = 220 V. Nhiệt độ ban đầu của nước là \({t_1}\) = 20° C, nhiệt dung riêng của nhôm là \({c_1}\) = 920 J/kg.K, của nước là \({c_2}\) = 4 200 J/kg.K. Tìm nhiệt lượng cần cung cấp cho ấm nước và cường độ dòng điện chạy qua bếp điện.
Phương pháp :
Công thức tính nhiệt lượng cần để tăng nhiệt : \(Q = mc\Delta t\)
Lời giải chi tiết :
Nhiệt lượng cần cung cấp cho ấm nước để đun sôi là :
\(Q = {Q_1} + {Q_2} = {m_1}{c_1}\left( {100 - {t_1}} \right) + {m_2}{c_2}\left( {100 - {t_2}} \right) = 0,4.920.\left( {100 - 20} \right) + 2.4200\left( {100 - 20} \right) = 701440J\)
=> Nhiệt lượng cần cung cấp cho ấm nước là : \({Q^'} = \frac{Q}{H} = \frac{{701440}}{{60\% }} = 1169066J\)
Cường độ dòng điện chạy qua bếp điện là : \(I = \frac{{{Q^'}}}{{U.t}} = \frac{{1169066}}{{220.20.60}} = 4,4A\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài tập cuối chương IV trang 64, 65, 66, 67 SBT Vật lí 11 Kết nối tri thức với cuộc sống timdapan.com"







