Bài 23. Điện trở. Định luật Ohm trang 53, 54, 55, 56, 57 SBT Vật lí 11 Kết nối tri thức với cuộc sống
Đơn vị đo điện trở là
23.1
Đơn vị đo điện trở là
A. ôm (\(\Omega \)).
B. fara (F)
G. henry (H).
D. oát (W).
Phương pháp :
Lí thuyết về điện trở .
Lời giải chi tiết :
Đơn vị đo điện trở là ôm (\(\Omega \)).
Đáp án :A
23.2
Phát biểu nào sau đây sai :
A. Điện trở có vạch màu là căn cứ để xác định trị số.
B. Đối với điện trở nhiệt có hệ số dương, khi nhiệt độ tăng thì điện trở tăng.
C. Đối với điện trở biến đổi theo điện áp, khi U tăng thì điện trở tăng.
D. Đối với điện trở quang, khi ánh sáng thích hợp rọi vào thì điện trở giảm.
Phương pháp :
Lí thuyết về điện trở .
Lời giải chi tiết :
Phát biểu nào sau đây sai là : Đối với điện trở biến đổi theo điện áp, khi U tăng thì điện trở tăng
Đáp án :C
23.3
Đặc điểm của điện trở nhiệt có hệ số nhiệt điện trở.
A. dương khi nhiệt độ tăng thì điện trở tăng.
B. dương khi nhiệt độ tăng thì điện trở giảm.
C. âm khi nhiệt độ tăng thì điện trở tăng.
D. âm khi nhiệt độ tăng thì điện trở giảm về bằng 0.
Phương pháp :
Lí thuyết về điện trở .
Lời giải chi tiết :
Đặc điểm của điện trở loại có hệ số dương là khi nhiệt độ tăng thì điện trở tăng, các nhiệt trở được làm bằng kim loại có hệ số nhiệt dương do khi nhiệt độ tăng, các nguyên tử nút mạng dao động mạnh làm cản trở quá trình di chuyển của electron nên giá trị điện trở tăng.
Đáp án :A
23.4
Nếu chiều dài và đường kính của một dây dẫn bằng đồng có tiết diện tròn được tăng lên gấp đôi thì điện trở của dây dẫn sẽ
A. không thay đổi.
B. tăng lên hai lần.
C. tăng lên gấp bồn lần.
D. giảm đi hai lần.
Phương pháp :
Công thức tính điện trở : \(R = \rho .\frac{l}{S}\)
Lời giải chi tiết :
Ta có : \(R = \rho .\frac{l}{S} = \frac{{4\rho l}}{{\pi {d^2}}}\) => tăng l và d lên 2 lần thì R giảm 2 lần .
Đáp án : D
23.5
Chọn biến đổi đúng trong các biền đổi sau.
A. \(1\Omega = 0,001k\Omega = 0,0001M\Omega \)
B. \(10\Omega = 0,1k\Omega = 0,00001M\Omega \).
G. \(1k\Omega = 1000\Omega = 0,01M\Omega \).
D. \(1{\rm M}\Omega = 1000k\Omega = 1000000\Omega \)
Phương pháp :
Một số bội số của ôm
Lời giải chi tiết :
Theo các bội số của ôm : \(1{\rm M}\Omega = 1000k\Omega = 1000000\Omega \)
Đáp án : D
23.6
Biến trở là
A. điện trở có thể thay đổi trị số và dùng để điều chỉnh chiều dòng điện trong mạch.
B. điện trở có thể thay đổi trị số và dùng để điều chỉnh cường độ và chiều dòng điện trong mạch.
C. điện trở có thể thay đổi trị số và dùng để điều chỉnh cường độ dòng điện
trong mạch.
D. điện trở không thay đồi trị số và dùng để điều chỉnh cường độ dòng điện
trong mạch.
Phương pháp :
Khái niệm của biến trở .
Lời giải chi tiết :
Biến trở là điện trở có thể thay đổi trị số và dùng để điều chỉnh cường độ dòng điện trong mạch.
Đáp án : C
23.7
Trước khi mắc biến trở vào mạch điện để điều chỉnh cường độ dòng điện thì cần điều chỉnh biến trở có giá trị nào dưới đây?
A. Có giá trị bằng 0.
B. Có giá trị nhỏ.
C. Có giá trilớn.
D. Có giá trị lớn nhất
Phương pháp :
Khái niệm của biến trở .
Lời giải chi tiết :
Trước khi mắc biến trở vào mạch để điều chỉnh cường độ dòng điện thì cần điều chỉnh biến trở có giá trị lớn nhất, như vậy cường độ dòng điện qua mạch sẽ nhỏ nhất.
Đáp án : D
23.8
Chọn phát biểu đúng về định luật Ohm.
A. Cường độ dòng điện chạy qua dây dẫn tỉ lệ với hiệu điện thế giữa hai đầu
dây dẫn và điện trở của dây.
B. Cường độ dòng điện chạy qua dây dẫn tỉ lệ thuận với hiệu điện thế giữa hai
đầu dây dẫn và không tỉ lệ với điện trở của dây.
C. Cường độ dòng điện chạy qua dây dẫn tỉ lệ thuận với hiệu điện thế giữa hai
đầu dây dẫn và tỉ lệ nghịch với điện trở của dây.
D. Cường độ dòng điện chạy qua dây dẫn tỉ lệ nghịch với hiệu điện thế giữa
hai đầu dây dẫn và tỉ lệ thuận với điện trở của dây.
Phương pháp :
Định luật Ohm
Lời giải chi tiết :
Cường độ dòng điện chạy qua dây dẫn tỉ lệ thuận với hiệu điện thế giữa hai
đầu dây dẫn và tỉ lệ nghịch với điện trở của dây
Đáp án : C
23.9
Biểu thức đúng của định luật Ohm là
A. \(I = \frac{R}{U}\)
B. \(I = \frac{U}{R}\)
C. \(U = \frac{I}{R}\)
D. \(U = \frac{R}{I}\)
Phương pháp :
Định luật Ohm
Lời giải chi tiết :
Biểu thức đúng của định luật Ohm là \(I = \frac{U}{R}\)
Đáp án :B
23.10
Khi hiệu điện thế giữa hai đầu dây dẫn tăng thì
A. cường độ dòng điện chạy qua dây dẫn không thay đổi.
B. cường độ dòng điện chạy qua dây dẫn giảm, tỉ lệ với hiệu điện thế.
C. cường độ dòng điện chạy qua dây dẫn có lúc tăng, có lúc giảm.
D. cường độ dòng điện chạy qua dây dẫn tăng, tỉ lệ với hiệu điện thế.
Phương pháp :
Biểu thức đúng của định luật Ohm là \(I = \frac{U}{R}\)
Lời giải chi tiết :
Cường độ dòng điện chạy qua dây dẫn tỉ lệ thuận với hiệu điện thế giữa hai
đầu dây dẫn => Khi hiệu điện thế giữa hai đầu dây dẫn tăng thì cường độ dòng điện chạy qua dây dẫn tăng, tỉ lệ với hiệu điện thế.
Đáp án :D
23.11
Đồ thị biểu diễn sự phụ thuộc của cường độ dòng điện vào hiệu điện thế giữa hai đầu dây dẫn có dạng là
A. một đường thẳng đi qua gốc toạ độ.
B. một đường cong đi qua gắc toạ độ.
C. một đường thẳng không đi qua gốc toạ độ.
D. một đường cong không đi qua gốc toạ độ.
Phương pháp :
Biểu thức đúng của định luật Ohm là \(I = \frac{U}{R}\)
Lời giải chi tiết :
Ta có biểu thức : \(I = \frac{U}{R}\) => Đồ thị biểu diễn sự phụ thuộc của cường độ dòng điện vào hiệu điện thế giữa hai đầu dây dẫn có dạng là một đường thẳng đi qua gốc toạ độ
Đáp án :A
23.12
Cường độ dòng điện chạy qua dây dẫn tỉ lệ thuận với hiệu điện thế giữa hai đầu dây dẫn. Nếu tăng hiệu điện thế lên 1,6 lần thì
A. cường độ dòng điện tăng 3,2 lần.
B. cường độ dòng điện giảm 3,2 lần.
C. cường độ dòng điện giảm 1,6 lần.
D. cường độ dòng điện tăng 1,6 lần.
Phương pháp :
Biểu thức đúng của định luật Ohm là \(I = \frac{U}{R}\)
Lời giải chi tiết :
Ta có biểu thức : \(I = \frac{U}{R}\) => Nếu tăng hiệu điện thế lên 1,6 lần thì cường độ dòng điện tăng 1,6 lần
Đáp án :D
23.13
Từ đồ thị biểu diễn sự phụ thuộc của cường độ dòng điện vào hiệu điện thế đối với hai điện trở \({R_1};{R_2}\) trong Hình 23.1 .Điện trở \({R_1};{R_2}\) có giá trị là
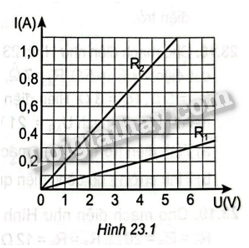
A. \({R_1} = 5\Omega ;{R_2} = 20\Omega \)
B. \({R_1} = 10\Omega ;{R_2} = 5\Omega \)
C. \({R_1} = 5\Omega ;{R_2} = 10\Omega \)
D. \({R_1} = 20\Omega ;{R_2} = 5\Omega \)
Phương pháp :
Biểu thức đúng của định luật Ohm là \(I = \frac{U}{R}\)
Lời giải chi tiết :
Ta có biểu thức : \(I = \frac{U}{R} = > R = \frac{U}{I}\)
Dựa vào đồ thị ta có : \({R_1} = \frac{{{U_1}}}{{{I_1}}} = \frac{4}{{0,2}} = 20\Omega \)
Tương tự ta có : \({R_2} = \frac{{{U_2}}}{{{I_2}}} = \frac{2}{{0,4}} = 5\Omega \)
Đáp án : D
23.14
Muốn đo hiệu điện thế giữa hai cực của một nguồn điện, nhưng không có vôn kế, một học sinh đã sử dụng một ampe kế và một điện trở có giá trị \(R = 50\Omega \) mắc nối tiếp nhau sau, đó mắc vào nguồn điện, biết ampe kế chỉ 1,2A. Hiệu điện thế giữa hai cực nguồn điện có giá trị bằng bao nhiêu?
A.120V.
B. 50V.
C.12V.
D. 60V.
Phương pháp :
Biểu thức đúng của định luật Ohm là \(I = \frac{U}{R}\)
Lời giải chi tiết :
Ta có biểu thức : \(I = \frac{U}{R} = > U = I.R = 50.1,2 = 60V\)
Đáp án : D
23.15
Cho mạch điện như Hình 23.2. Các giá tị điện trở \({R_1} = 6\Omega \), \({R_2} = 4\Omega \), \({R_3} = 2\Omega \), \({R_4} = 3\Omega \), \({R_5} = 6\Omega \)
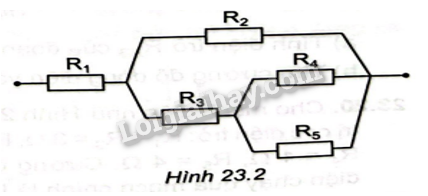
a) Tính hiệu điện thế giữa hai đầu điện trở \({R_2}\) nếu cường độ dòng điện qua
điện trở \({R_1}\)có giá trị 1A.
b) Tính hiệu điện thế giữa hai đầu điện trở \({R_2}\)nếu cường độ dòng điện qua
điện trở \({R_5}\) có giá trị 1A.
Phương pháp :
Vận dụng kiến thức định luật Ohm trong các đoạn mạch .
Lời giải chi tiết :
a) Theo hình vẽ ta có : \({R_1}\) nt \({R_{2345}}\)=> cường độ dòng điện \({I_1} = {I_{2345}} = 1A\)
Ta có : \({R_4}\)//\({R_5}\) => \({R_{45}} = \frac{{{R_4}.{R_5}}}{{{R_4} + {R_5}}} = \frac{{3.6}}{{3 + 6}} = 2\Omega \)
Tương tự \({R_3}\) nt \({R_{45}}\)=> \({R_{345}} = {R_3} + {R_{45}} = 2 + 2 = 4\Omega \)
Tương tự \({R_2}\)// \({R_{345}}\)=> \({R_{2345}} = 2\Omega \)=> \({U_{2345}} = {I_{2345}}.{R_{2345}} = 1.2 = 2V\)
=> \({U_2} = {U_{2345}} = 2V\) => hiệu điện thế giữa hai đầu điện trở \({R_2}\) nếu cường độ dòng điện qua điện trở \({R_1}\)có giá trị 1A là 2V
b) Theo đề bài ta có \({I_5} = 1A = > {U_5} = {I_5}.{R_5} = 6V\)
mà ta có \({R_4}\)//\({R_5}\) => \({U_{45}} = {U_5} = 6V = > {I_{45}} = \frac{{{U_{45}}}}{{{R_{45}}}} = \frac{6}{2} = 3A\)
Tương tự \({R_3}\) nt \({R_{45}}\)=>\({I_3} = {I_{45}} = 3A = > {U_3} = {R_3}.{I_3} = 2.3 = 6V\)
=> \({U_{345}} = {U_3} + {U_{45}} = 6 + 6 = 12V\)
Tương tự \({R_2}\)// \({R_{345}}\)=> \({U_2} = {U_{345}} = 12V\) => hiệu điện thế giữa hai đầu điện trở \({R_2}\)nếu cường độ dòng điện qua điện trở \({R_5}\) có giá trị 1A là 12V.
23.16
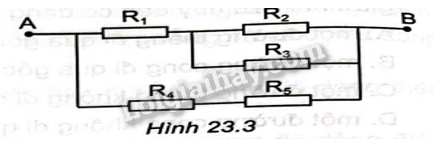
Cho một đoạn mạch điện như Hình 23.3. Biết các giá trị điện trở: \({R_1} = 1\Omega \),\({R_2} = 20\Omega \),\({R_3} = 5\Omega \), \({R_4} = {R_5} = 10\Omega \) . Hãy tính điện trở của đoạn mạch AB.
Phương pháp :
Vận dụng kiến thức định luật Ohm trong các đoạn mạch .
Lời giải chi tiết :
Theo hình vẽ ta có : \({R_2}\)// \({R_3}\) => \({R_{23}} = \frac{{{R_2}.{R_3}}}{{{R_2} + {R_3}}} = \frac{{20.5}}{{20 + 5}} = 4\Omega \)
Tương tự ta có : \({R_1}\) nt \({R_{23}}\)=> \({R_{123}} = {R_1} + {R_{23}} = 1 + 4 = 5\Omega \)
Ta lại có \({R_4}\) nt \({R_5}\)=> \({R_{45}} = 20\Omega \)
Tương tự \({R_{123}}\)// \({R_{45}}\)=> \({R_{AB}} = \frac{{{R_{123}}.{R_{45}}}}{{{R_{123}} + {R_{45}}}} = \frac{{20.5}}{{20 + 5}} = 4\Omega \)
23.17
Cho mạch điện như Hình 23.4. Biết các giá trị điện trở: \({R_1} = 2\Omega \),\({R_2} = 3\Omega \),\({R_3} = 4\Omega \), \({R_4} = 6\Omega \). Hiệu điện thế giữa hai đầu đoạn mạch \({U_{AB}} = 18V\)
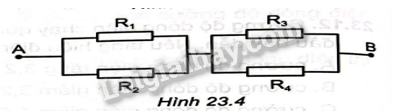
a)Tính điện trở của đoạn mạch AB.
b) Tìm cường độ dòng điện chạy qua các điện trở và hiệu điện thể trên mỗi
điện trở.
Phương pháp :
Vận dụng kiến thức định luật Ohm trong các đoạn mạch .
Lời giải chi tiết :
a) Theo hình vẽ ta có \({R_1}\) // \({R_2}\)=> \({R_{12}} = \frac{{{R_1}.{R_2}}}{{{R_1} + {R_2}}} = \frac{{2.3}}{{2 + 3}} = 1,2\Omega \)
Tương tự ta có \({R_3}\) // \({R_4}\)=>\({R_{34}} = 2,4\Omega \)
Ta lại có \({R_{12}}\) nt \({R_{34}}\) => điện trở của đoạn mạch AB \({R_{AB}} = {R_{12}} + {R_{34}} = 1,2 + 2,4 = 3,6\Omega \)
b) Ta có \({I_{AB}} = \frac{{{U_{AB}}}}{{{R_{AB}}}} = \frac{{18}}{{3,6}} = 5A\)
mà ta có \({R_{12}}\) nt \({R_{34}}\)=> \({I_{12}} = {I_{34}} = 5A\)
hiệu điện thế \({U_{12}} = {I_{12}}.{R_{12}} = 5.1,2 = 6V\) mà ta có \({R_1}\) // \({R_2}\)=> \({U_1} = {U_2} = {U_{12}} = 6V\)
=> Cường độ dòng điện qua \({R_1}\) là : \({I_1} = \frac{{{U_1}}}{{{R_1}}} = \frac{6}{2} = 3A\)
=> Cường độ dòng điện qua \({R_2}\) là : \({I_2} = \frac{{{U_2}}}{{{R_2}}} = \frac{6}{3} = 2A\)
Tương tự ta có \({U_{34}} = {I_{34}}.{R_{34}} = 5.2,4 = 12V\)mà ta có \({R_3}\) // \({R_4}\)=>\({U_3} = {U_4} = {U_{34}} = 12V\)
=> Cường độ dòng điện qua \({R_3}\) là : \({I_3} = \frac{{{U_3}}}{{{R_3}}} = \frac{{12}}{4} = 3A\)
=> Cường độ dòng điện qua \({R_4}\) là : \({I_4} = \frac{{{U_4}}}{{{R_4}}} = \frac{{12}}{6} = 2A\)
23.18
Cho mạch điện như Hình 23.5. Giá trịcác điện trở: \({R_1} = 5\Omega \),\({R_2} = 7\Omega \),\({R_3} = 1\Omega \), \({R_4} = 5\Omega \),\({R_5} = 3\Omega \). Hiệu điện thế giữa hai đầu đoạn mạch \({U_{AB}} = 21V\)
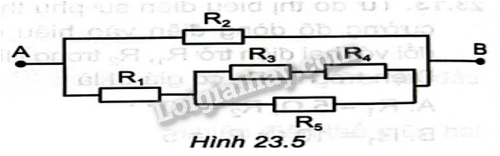
a) Tính điện trở của đoạn mạch AB (\({R_{AB}}\))
b) Tính cường độ dòng điện qua các điện trở.
Phương pháp :
Vận dụng kiến thức định luật Ohm trong các đoạn mạch .
Lời giải chi tiết :
a) Ta có : \({R_3}\) nt \({R_4}\)=> \({R_{34}} = {R_3} + {R_4} = 1 + 5 = 6\Omega \)
\({R_5}//{R_{34}} = > {R_{345}} = \frac{{{R_{34}}.{R_5}}}{{{R_{34}} + {R_5}}} = \frac{{6.3}}{{6 + 3}} = 2\Omega \)
Ta lại có : \({R_1}nt{R_{345}} = > {R_{1345}} = {R_1} + {R_{345}} = 2 + 5 = 7\Omega \)
Và \({R_2}//{R_{1345}}\)=> điện trở của đoạn mạch AB : \({R_{AB}} = \frac{{{R_2}.{R_{1345}}}}{{{R_2} + {R_{1345}}}} = 3,5\Omega \)
b) Ta có \({R_2}//{R_{1345}} = > {U_2} = {U_{1345}} = {U_{AB}} = 21V\)=> cường độ dòng điện qua điện trở \({R_2}\)là \({I_2} = \frac{{{U_2}}}{{{R_2}}} = \frac{{21}}{7} = 3A\)
ta có \({I_{1345}} = \frac{{{U_{1345}}}}{{{R_{1345}}}} = \frac{{21}}{7} = 3A\) mà ta có \({R_1}\) nt \({R_{345}}\)=> \({I_1} = {I_{345}} = 3A\)
cường độ dòng điện qua điện trở \({R_1}\)là 3A
Hiệu điện thế \({U_{345}} = {I_{345}}.{R_{345}} = 3.2 = 6V\)mà \({R_5}//{R_{34}} = > {U_{34}} = {U_5} = {U_{345}} = 6V\)
=> cường độ dòng điện qua điện trở \({R_5}\)là \({I_5} = \frac{{{U_5}}}{{{R_5}}} = \frac{6}{3} = 2A\)
Ta có \({I_{34}} = \frac{{{U_{34}}}}{{{R_{34}}}} = \frac{6}{6} = 1A\) mà \({R_3}\) nt \({R_4}\)=> \({I_3} = {I_4} = 1A\)
23.19
Cho mạch điện như Hình 23.6. Cho biết cáo giá trị điện trở: \({R_1} = 4\Omega \),
\({R_2} = {R_5} = 20\Omega \), \({R_3} = {R_6} = 12\Omega \),\({R_4} = {R_7} = 8\Omega \). Hiệu điện thể giữa hai đầu đoạn
mạch \({U_{AB}} = 48V\)
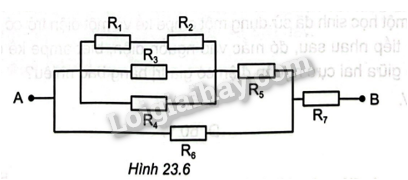
a) Tính điện trở \({R_{AB}}\) của đoạn mạch AB.
b) Tìm cường độ dòng điện và hiệu điện thể của mỗi điện trở.
Phương pháp :
Vận dụng kiến thức định luật Ohm trong các đoạn mạch .
Lời giải chi tiết :
a) Ta có \({R_1}nt{R_2} = > {R_{12}} = {R_1} + {R_2} = 4 + 20 = 24\Omega \)
\({R_3}//{R_4} = > {R_{34}} = \frac{{{R_3}.{R_4}}}{{{R_3} + {R_4}}} = 4.8\Omega \) và ta có \({R_{12}}//{R_{34}} = > {R_{1234}} = 4\Omega \)
Ta lại có : \({R_5}nt{R_{1234}} = > {R_{12345}} = {R_5} + {R_{1234}} = 4 + 20 = 24\Omega \)
Tương tự \({R_6}//{R_{12345}} = > {R_{123456}} = 8\Omega \) và \({R_7}nt{R_{123456}}\)=> điện trở \({R_{AB}}\) của đoạn mạch AB \({R_{AB}} = {R_7} + {R_{123456}} = 8 + 8 = 16\Omega \)
b) ta có \({I_{AB}} = \frac{{{U_{AB}}}}{{{R_{AB}}}} = \frac{{48}}{{16}} = 3A\) mà \({R_7}nt{R_{123456}} = > {I_7} = {I_{123456}} = 3A\)
=> hiệu điện thế \({U_7} = {I_7}.{R_7} = 3.8 = 24V\)
Ta có \({U_{123456}} = {U_{AB}} - {U_7} = 48 - 24 = 24V\)mà ta có \({R_6}//{R_{12345}} = > {U_6} = {U_{12345}} = 24V\)
=> Cường độ dòng điện : \({I_6} = \frac{{{U_6}}}{{{R_6}}} = \frac{{24}}{{12}} = 2A\)
Ta có : \({I_{12345}} = \frac{{{U_{12345}}}}{{{R_{12345}}}} = \frac{{24}}{{24}} = 1A\)mà \({R_5}nt{R_{1234}} = > {I_5} = {I_{1234}} = 1A\)
=> hiệu điện thế \({U_5} = {I_5}.{R_5} = 1.20 = 20V = > {U_{1234}} = {U_{12345}} - {U_5} = 24 - 20 = 4V\)
Mà \({R_{12}}//{R_{34}} = > {U_{12}} = {U_{34}} = 4V\) mà => \({I_3} = \frac{{{U_3}}}{{{R_3}}} = \frac{4}{{12}} = \frac{1}{3}A\) và \({I_4} = \frac{{{U_4}}}{{{R_4}}} = \frac{4}{8} = \frac{1}{2}A\)
Ta có \({I_{12}} = \frac{{{U_{12}}}}{{{R_{12}}}} = \frac{4}{{24}} = \frac{1}{6}A\) mà \({R_1}nt{R_2} = > {I_1} = {I_2} = \frac{1}{6}A\)
=> \({U_1} = {I_1}.{R_1} = \frac{1}{6}.4 = \frac{2}{3}V\) và \({U_2} = {I_2}.{R_2} = \frac{1}{6}.20 = \frac{{10}}{3}V\)
23.20
Cho mạch điện như Hình 23.7. Giá trị các điện trở: \({R_1} = {R_3} = 3\Omega \),\({R_2} = 2\Omega \),\({R_4} = 1\Omega \),\({R_5} = 4\Omega \). Cường độ dòng điện chạy qua mạch chính là \(I = 3A\)
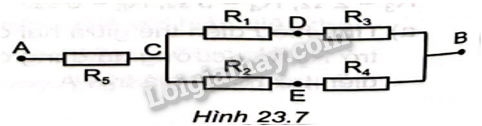
Tính:
a) Hiệu điện thế giữa hai đầu đoạn mạch \({U_{AB}}\) và hiệu điện thế của mỗi điện trở.
b) Hiệu điện thế giữa hai điểm A và D; E và D.
Phương pháp :
Vận dụng kiến thức định luật Ohm trong các đoạn mạch .
Lời giải chi tiết :
a) Theo hình ta có : \({R_1}nt{R_3} = > {R_{13}} = {R_1} + {R_3} = 3 + 3 = 6\Omega \)
Tương tự :\({R_2}nt{R_4} = > {R_{24}} = 3\Omega \)
Mà ta có : \({R_{13}}//{R_{24}} = > {R_{1234}} = \frac{{{R_{13}}.{R_{24}}}}{{{R_{13}} + {R_{24}}}} = 2\Omega \)
\({R_5}nt{R_{1234}} = > {R_{AB}} = {R_5} + {R_{1234}} = 4 + 2 = 6\Omega \)
=> Hiệu điện thế giữa hai đầu đoạn mạch \({U_{AB}} = {I_{AB}}.{R_{AB}} = 3.6 = 18V\)
Ta có \({R_5}\) nt \({R_{1234}}\) => \({I_5} = {I_{1234}} = 3A = > {U_5} = {I_5}.{R_5} = 3.4 = 12V = > {U_{1234}} = {U_{AB}} - {U_5} = 18 - 12 = 6V\)
Mà ta có : \({R_{13}}//{R_{24}} = > {U_{13}} = {U_{24}} = 6V\)
Ta có \({I_{13}} = \frac{{{U_{13}}}}{{{R_{13}}}} = \frac{6}{6} = 1A\) mà \({R_1}nt{R_3} = > {I_1} = {I_3} = 1A\)
=> hiệu điện thế \({U_1} = {I_1}.{R_1} = 1.3 = 3V\) và \({U_3} = {I_3}.{R_3} = 1.3 = 3V\)
Tương tự ta có : \({I_{24}} = \frac{{{U_{24}}}}{{{R_{24}}}} = \frac{6}{3} = 2A\) mà \({R_2}nt{R_4} = > {I_2} = {I_4} = 2A\)
=> hiệu điện thế \({U_2} = {I_2}.{R_2} = 2.2 = 4V\) và \({U_4} = {I_4}.{R_4} = 2.1 = 2V\)
b) Trong đoạn dây AD có \({U_{AD}} = {U_{AC}} + {U_{CD}} = > {U_{AD}} = {U_5} + {U_1} = 12 + 3 = 15V\)
trong đoạn dây ED có \(\)\({U_{ED}} = {U_{EC}} + {U_{CD}} = {U_2} - {U_1} = 4 - 3 = 1V\)
23.21
Cho mạch điện như Hình 23.8. Giá trị các điện trở:\({R_1} = {R_3} = {R_5} = 1\Omega \)
\({R_4} = 2\Omega \),\({R_2} = 3\Omega \). Biết dòng điện chạy qua điện trở \({R_4}\) là 1A
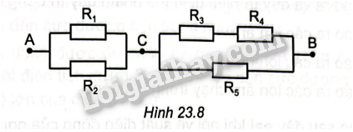
a) Tính điện trở của đoạn mạch AB.
b) Tính cường độ dòng điện qua các điện trở.
c) Tính hiệu điện thế giữa hai đàu đoạn mạch AB.
Phương pháp :
Vận dụng kiến thức định luật Ohm trong các đoạn mạch .
Lời giải chi tiết :
a) Theo hình ta có R \({R_1}//{R_2} = > {R_{12}} = \frac{{{R_1}.{R_2}}}{{{R_1} + {R_2}}} = \frac{3}{4}\Omega \)
Tương tự \({R_3}nt{R_4} = > {R_{34}} = {R_3} + {R_4} = 1 + 2 = 3\Omega \)
Và \({R_{34}}//{R_5} = > {R_{345}} = \frac{{{R_{34}}.{R_5}}}{{{R_{34}} + {R_5}}} = \frac{3}{4}\Omega \)
\({R_{12}}\) nt \({R_{345}}\) => điện trở của đoạn mạch AB =>\({R_{AB}} = {R_{12}} + {R_{345}} = \frac{3}{4} + \frac{3}{4} = 1,5\Omega \)
b) ta có \({R_3}nt{R_4} = > {I_3} = {I_{34}} = {I_4} = 1A = > {U_{34}} = {I_{34}}.{R_{34}} = 3.1 = 3V\)
ta có \({R_{34}}//{R_5} = > {U_5} = {U_{345}} = {U_{34}} = 3V = > {I_5} = \frac{{{U_5}}}{{{R_5}}} = \frac{3}{1} = 3A\)
mà ta có \({I_{345}} = {I_{34}} + {I_5} = 1 + 3 = 4A\) mà \({R_{12}}\) nt \({R_{345}}\)=> \({I_{12}} = {I_{345}} = 4A = > {U_{12}} = {I_{12}}.{R_{12}} = 4.\frac{3}{4} = 3V\) mà \({R_1}//{R_2} = > {U_1} = {U_2} = 3V\)
=> cường độ dòng điện \({I_1} = \frac{{{U_1}}}{{{R_1}}} = \frac{3}{1} = 3A\) và \({I_2} = \frac{{{U_2}}}{{{R_2}}} = \frac{3}{3} = 1A\)
c) ta có \({R_{12}}\) nt \({R_{345}}\) => hiệu điện thế giữa hai đàu đoạn mạch AB là
\({U_{AB}} = {U_{12}} + {U_{345}} = 3 + 3 = 6V\)
23.22
Cho mạch điện như Hình 23.9. Hiệu điện thể giữa hai đầu đoạn mạch.
AB là\({U_{AB}} = 6V\). Khi K mở ampe kế \({A_1}\) chỉ 1,2A. Khi K đóng, ampe kế \({A_1}\) và \({A_2}\) chỉ lần lượt 14A và 0,5A. Bỏ qua điện trở của các ampe kế.
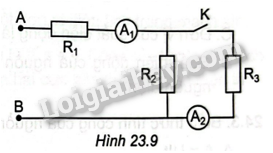
Tính điện trở: \({R_1},{R_2},{R_3}\)
Phương pháp :
Vận dụng kiến thức định luật Ohm trong các đoạn mạch .
Lời giải chi tiết :
Khi K mở thì \({R_1}\) nt \({R_2}\)=> \({R_1} + {R_2} = \frac{{{U_{AB}}}}{{{I_{{a_1}}}}} = \frac{6}{{1,2}} = 5\Omega \)
Khi K đóng : \({R_1}\) nt \(({R_2}//{R_3})\) => \({I_2} = {I_{{a_1}}} - {I_{{a_2}}} = 1,4 - 0,5 = 0,9A\)
Ta có : \({U_2} = {I_2}{R_2} = {U_{AB}} - {I_1}{R_1} = > 0,9{R_2} = 6 - 1,4{R_1} = > 0,9(5 - {R_1}) = 6 - 1,4{R_1}\)
=> \(4,5 - 0,9{R_1} = 6 - 1,4{R_1} = > 0,5{R_1} = 1,5 = > {R_1} = 3\Omega \)
=> \({R_2} = 5 - {R_1} = 5 - 3 = 2\Omega \)
Mà ta có : \({U_2} = {I_2}{R_2} = {U_{AB}} - {I_1}{R_1} = > 0,9{R_2} = 0,9.2 = 1,8V = > {U_3} = {U_2} = 1,8V = > {R_3} = \frac{{{U_3}}}{{{I_{{a_2}}}}} = \frac{{1,8}}{{0,5}} = 3,6\Omega \)
23.23
Cho mạch điện như Hình 23.10. Cho biết \({R_1} = 15\Omega \),\({R_2} = {R_3} = {R_4} = 10\Omega \). Điện trở của ampe kế và các dây nối không đáng kể.
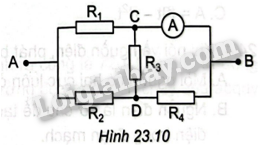
a) Tìm điện trở của đoạn mạch AB.
b) Biết ampe kế chỉ 3 A. Tính hiệu điện thế \({U_{AB}}\) và cường độ dòng điện chạy
qua các điện trở.
Phương pháp :
Vận dụng kiến thức định luật Ohm trong các đoạn mạch .
Lời giải chi tiết :
Ampe kế có điện trở không đáng kể nên C và B cùng điện thế , chấp C và B ta có đoạn mạch mới .
Từ đoạn mạch ta có \(\)\({R_1}//\left[ {{R_2}nt\left( {{R_3}//{R_4}} \right)} \right]\)
Ta có \({R_{34}} = \frac{{{R_3}.{R_4}}}{{{R_3} + {R_4}}} = 5\Omega \) ;\({R_{234}} = {R_2} + {R_{34}} = 10 + 5 = 15\Omega \)
=> điện trở của đoạn mạch AB \({R_{AB}} = \frac{{{R_{234}}.{R_1}}}{{{R_{234}} + {R_1}}} = 7,5\Omega \)
Do \({U_3} = {U_4}\) và \({R_3} = {R_4}\)=> \({I_3} = {I_4}\)
Do \({R_2}nt{R_{34}} = > {I_2} = {I_3} + {I_4} = 2{I_3}\) mà ta có\({U_{AB}} = {I_2}.{R_{234}} = {I_1}.{R_1} = > 2{I_3}.15 = {I_1}.15 = > {I_3} = 0,5{I_1}\)(1)
Giả sử dòng đi từ D đến C
Xét tại nút C : \({I_A} = {I_1} + {I_3} = 3A\) (2)
Từ (1) và (2) => \({I_1} = 2A\) và \({I_3} = 1A = {I_4}\)=> hiệu điện thế \({U_{AB}} = {I_1}.{R_1} = 2.15 = 30V\)
=> \({I_2} = 2{I_3} = 2A\)
23.2
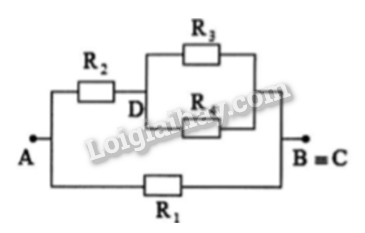
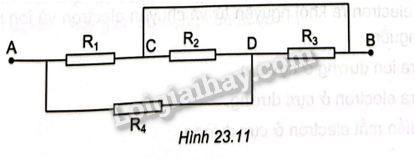
Cho đoạn mạch như Hình 23.11. Tính điện trở của đoạn mạch AB, biết các điện trở có giá trị bằng nhau và bằng R. Biết dây nối có điện trở không đáng kể.
Phương pháp :
Vận dụng kiến thức định luật Ohm trong các đoạn mạch .
Lời giải chi tiết :
Chập B với C ta có đoạn mạch mới :
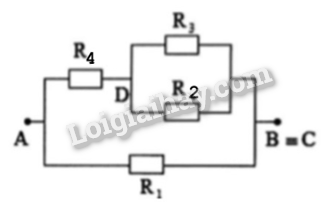
Theo hình vẽ ta có : \({R_1}//\left[ {{R_4}nt\left( {{R_2}//{R_3}} \right)} \right]\)
Ta có \({R_{23}} = \frac{{{R_2}.{R_3}}}{{{R_2} + {R_3}}} = \frac{{R.R}}{{R + R}} = 1,5R\Omega \) và \({R_{234}} = {R_2} + {R_{34}} = 1,5R\Omega \)
=> điện trở của đoạn mạch AB \({R_{AB}} = \frac{{{R_1}.{R_{234}}}}{{{R_1} + {R_{234}}}} = \frac{{R.1,5R}}{{R + 1,5R}} = 0,6R\Omega \)
Search google: "từ khóa + timdapan.com" Ví dụ: "Bài 23. Điện trở. Định luật Ohm trang 53, 54, 55, 56, 57 SBT Vật lí 11 Kết nối tri thức với cuộc sống timdapan.com"