Ôn tập chương II trang 22, 23, 24 SBT Vật lí 10 Kết nối tri thức với cuộc sống

II.1

Trường hợp nào sau đây có thể xác định được vận tốc của chuyển động?

A. Ô tô chạy từ Hà Nội về Nam Định hết 1 giờ 30 phút và chạy được 90 km.

B. Vận động viên bơi trong bể bơi được 1500m hết 20 phút.

C. Chim bồ câu đưa thư bay thẳng theo hướng bắc, từ nơi được thả ra về chuồng cách nhau 80 km hết 2 giờ.

D. Người tập đi bộ quanh công viên trong 1 giờ đi được 7 km.

Phương pháp giải:

Dựa vào khái niệm vận tốc

Lời giải chi tiết:

Vận tốc là đại lượng vật lý có hướng (véctơ) cùng hướng với độ dời \(\overrightarrow {\Delta x} \)được xác định trong khoảng thời gian \(\Delta t\).

Vì vậy trong các đáp án trên chỉ có đáp án C là có hướng và xác định được độ dời và thời gian chuyển động.

Chọn đáp án C.

---

II.2

Hai vật được đồng thời ném lên từ cùng một độ cao với vận tốc ban đầu có cùng độ lớn và có phương vuông góc với nhau (Hình II.1).

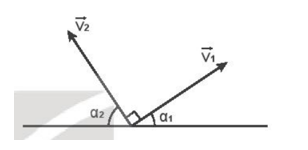
A. Hai vật có tầm bay xa bằng nhau.

B. Hai vật có tầm bay cao bằng nhau.

C. Vật 2 có tầm bay xa lớn hơn vật 1.

D. Vật 1 rơi tới đất sau vật 2.

Phương pháp giải:

Dựa vào công thức tính tầm bay cao và tầm bay xa của vật được ném xiên:

Tầm cao: H = d_ymax = \(\frac{{v_{0y}^2}}{{2g}}\) = \(\frac{{v_0^2.{{\sin }^2}\alpha }}{{2g}}\)

Tầm xa: L = d_xmax =  \(\frac{{v_{0x}^2}}{g}\) = \(\frac{{v_0^2.{{\sin }^2}2\alpha }}{g}\)

Lời giải chi tiết:

Ta có: α₁ + α₂ = 90^o => 2α₁ = 180^o - 2α₂ => sin 2α₁ = sin 2α₂.

Khi đó: L₁ = \(\frac{{v_0^2.{{\sin }^2}2{\alpha _1}}}{g}\); L₂ = \(\frac{{v_0^2.{{\sin }^2}2{\alpha _2}}}{g}\)

=> L₁ = L₂.

Ta có: 0 < α₁ < α₂ < 90^o => 0 < sin α₁ < sinα₂ < 1.

Và |v₀₁| = |v₀₂|

=> \(\frac{{v_{01}^2.{{\sin }^2}{\alpha _1}}}{{2g}}\) < \(\frac{{v_{02}^2.{{\sin }^2}{\alpha _2}}}{{2g}}\)=> H₁ < H₂.

Vậy 2 vật có tầm bay xa bằng nhau, tầm bay xa khác nhau, vật 1 có tầm bay cao nhỏ hơn nên sẽ rơi tới đất trước vật 2.

Chọn đáp án B.

---

II.3

Hình II.2 là đồ thị độ dịch chuyển - thời gian của chuyển động của một xe máy đi giao hàng online chạy trên đường thẳng. Xe khởi hành từ địa điểm cách nơi nhận hàng 200 m về phía bắc.

 

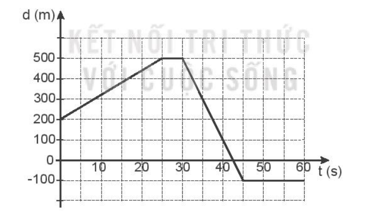
1. a) Trong khoảng thời gian nào xe đi về phía bắc?

b) Trong khoảng thời gian nào xe đi về phía nam?

c) Trong khoảng thời gian nào xe dừng lại?

2. Tỉnh tốc độ trung bình và vận tốc trung bình của xe trong 60 s.

Phương pháp giải:

1. Quan sát đặc điểm đồ thị để trả lời.

2. Biểu thức tính tốc độ trung bình: ϑ = \(\frac{s}{t}\)

Biểu thức tính vận tốc trung bình: v_tb = \(\frac{{\Delta d}}{{\Delta t}}\)

Trong đó:

+ ϑ: tốc độ chuyển động của vật (m/s)

+ s: quãng đường đi được của vật (m)

+ t: thời gian đi được quãng đường s của vật (s)

+ \(\Delta d\): Độ dịch chuyển (m)

+ \(\Delta t\): thời gian chuyển động khoảng

Lời giải chi tiết:

1. a) Từ 0 đến 25 s: xe đi về hướng bắc.

b) Từ 30 s đến 45 s: xe đi về hướng nam.

c) Từ 25 s đến 30 s và từ 45 s đến 60 s: xe không chuyển động.

2. Chọn chiều dương theo hướng nam - bắc:

Tốc độ trung bình của xe là: ϑ = \(\frac{s}{t}\)= \(\frac{{300 + 600}}{{60}}\)= \(\frac{{900}}{{60}}\)= 15 m/s.

Vận tốc trung bình của xe là: v_tb = \(\frac{{300 - 600}}{{60}}\)= \(\frac{{ - 300}}{{60}}\)= -5 m/s.

---

II.4

Một đoàn tàu cao tốc đang chạy thẳng với vận tốc 50 m/s thì người lái tàu giảm vận tộc của đoàn tàu với gia tốc có độ lớn không đổi 0,5 m/s² trong 100 s

a) Mô tả chuyển động của đoàn tàu.

b) Tính quãng đường đoàn tàu chạy được trong thời gian trên.

Phương pháp giải:

- Viết phương trình chuyển động của đoàn tàu:

v = v₀ + at; s = v₀t + \(\frac{1}{2}\)at².

Lời giải chi tiết:

a) Ta có: v = v₀ + at = 50 – 0,5.100 = 0.

=> Đoàn tàu chuyển động chậm dần đều, sau 100 s thì dừng lại.

b) Lại có: s = v₀t + \(\frac{1}{2}\)at² = 50.100 - \(\frac{1}{2}\).0,5.100² = 2500 m.

Vậy quãng đường đoàn tàu chạy được trong thời gian trên là 2500 m.

---

II.5

Hình II.3 là đồ thị vận tốc – thời gian của hai ô tô A và B cùng chạy theo một hướng trong 40 s. Xe A vượt qua xe B tại thời điểm t = 0. Để bắt kịp xe A, xe B tăng tốc trong 20 s để đạt vận tốc 50 m/s.

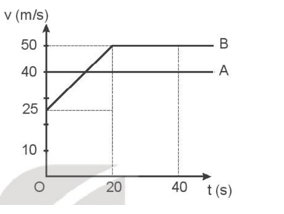
a) Tính độ dịch chuyển của xe A trong 20s.

b) Tính gia tốc của xe B trong 20 s.

c) Sau bao lâu thì xe B đuổi kịp xe A.

d) Tính quãng đường mỗi xe đi được trong 40 s và khi hai xe gặp nhau.

Phương pháp giải:

a) Ta thấy xe A chuyển động thẳng đều nên d_A = v_At_A.

b) Sử dụng công thức tính gia tốc: a = \(\frac{{\Delta {v_B}}}{{\Delta t}}\).

c) Viết phương trình chuyển động của xe B:

d_B = d_B1 + d_B2 =  v_0Bt + \(\frac{1}{2}\)at_B² + v_B(t_B – 20)

Hai xe gặp nhau khi d_A = d_B.

d) Thay số vào phương trình độ dịch chuyển của mỗi xe.

Lời giải chi tiết:

a) Hai xe chuyển động thẳng không đổi chiều nên d = s và v =ϑ.

Ta có xe A chuyển động thẳng đều nên d_A = v_At_A = 40.20 = 800 m.

b) Gia tốc của xe B trong 20 s là: a = \(\frac{{\Delta {v_B}}}{{\Delta t}}\)= \(\frac{{50 - 25}}{{20}}\)= 1,25 m/s².

c)

Ta có: d_A = v_At = 40t                (1)

d_B = d_B1 + d_B2.

Mà d_B1 = v_0Bt_B + \(\frac{1}{2}\)at_B² = 25.20 + \(\frac{1}{2}\).1,25.20² = 750 m.

=> Trong 20 s đầu 2 xe chưa gặp nhau.

Có d_B2 = v_B(t – 20) = 50(t – 20).

=> d_B = 750 + 50(t – 20).          (2)

Khi B đuổi kịp A thì d_A = d_B ⬄ 40t = 750 + 50(t – 20) => t = 25 s.

d) Quãng đường xe A đi được trong 40 s là: d_A = v_At = 40t = 40.40 = 1600 m.

Quãng đường xe B đi được trong 40 s là:

d_B = 750 + 50(t – 20) = 750 + 50(40 – 20) = 1750 m.

Thế t = 25 s vào (1), (2) ta được:

Khi hai xe gặp nhau, hai xe đi được quãng đường là d_A = d_B = 1000 m.

---

II.6

Một cầu thủ tennis ăn mừng chiến thắng bằng cách đánh quả bóng lên trời theo phương thẳng đứng với vận tốc lên tới 30 m/s. Bỏ qua sức cản của không khí và lấy g =10 m/s².

a) Tính độ cao cực đại mà bóng đạt được.

b) Tính thời gian từ khi bóng đạt độ cao cực đại tới khi trở về vị trí được đánh lên.

c) Tính vận tốc của bóng ở thời điểm t = 5s kể từ khi được đánh lên.

d) Vẽ đồ thị vận tốc - thời gian và gia tốc - thời gian của chuyển động của bóng.

Phương pháp giải:

a) Sử dụng công thức liên hệ giữa vận tốc, gia tốc và quãng đường: v² – v₀² = 2gh

=> h = -\(\frac{{v_0^2}}{{2g}}\).

b) Thời gian từ khi bóng đạt độ cao cực đại tới khi trở về vị trí được đánh lên bằng thời gian bóng rơi từ độ cao cực đại về vị trí ban đầu.

Áp dụng công thức: \(v = {v_0} + gt\) => t.

c) Sử dụng công thức tính vận tốc: \(v = {v_0} + gt\).

d) Từ các dữ kiện thu được, vẽ đồ thị vận tốc - thời gian và gia tốc - thời gian của chuyển động của bóng

Lời giải chi tiết:

Chọn hệ trục tọa độ có gốc O là vị trí bóng tiếp xúc với vợt và bắt đầu chuyển động, chiều dương là chiều từ dưới lên (Oy) và chiều từ trái sang phải (Ox).

a) Độ cao cực đại mà bóng đạt được là:

Ta sử dụng công thức liên hệ giữa vận tốc, gia tốc và quãng đường:

\({v_y}^2--{\rm{ }}{v_{0y}}^2 = {\rm{ }}2gh\) => h = -\(\frac{{v_{0y}^2}}{{2g}}\)= 45 m.

b) Thời gian từ khi bóng đạt độ cao cực đại tới khi trở về vị trí được đánh lên bằng thời gian bóng rơi từ độ cao cực đại về vị trí ban đầu.

Tại vị trí bóng đạt độ cao cực đại: v_y = 0.

Ta có: \({v_y} = {v_{0y}} + gt = 0\) => t = -\(\frac{{{v_{0y}}}}{g}\)= 3 s.

c)

Vì từ khi được đánh lên bóng mất 3s để đạt độ cao cực đại nên tại thời điểm t = 5s, bóng đang rơi xuống.

Vận tốc của bóng ở thời điểm t = 5s kể từ khi được đánh lên là:

v₅ = v_0y + gt₅ = 30 + (-10).5 = -20 m/s.

d)

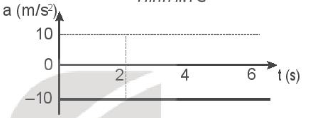
- Đồ thị vận tốc - thời gian

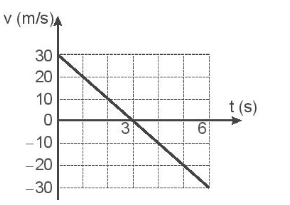
- Đồ thị gia tốc - thời gian

---

II.7

Một quả bóng quần vợt được thả ra từ một khinh khí cầu đang bay lên theo phương thẳng đứng với vận tốc 7,5 m/s. Bóng rơi chạm đất sau 2,5 s. Bỏ qua sức cản của không khí và lấy g = 10 m/s².

a) Mô tả chuyển động của bóng.

b) Vẽ đồ thị vận tốc - thời gian của bóng.

c) Xác định thời điểm bóng đạt độ cao cực đại.

d) Tính quãng đường đi được của bóng từ khi được thả ra tới khi đạt độ cao

cực đại.

e) Độ cao cực đại của bóng cách mặt đất bao nhiêu?

Phương pháp giải:

a) Từ các dữ kiện bài cho, phán đoán và mô tả của chuyển động của bóng.

b) Vẽ đồ thị vận tốc – thời gian của bóng từ các dữ kiện bài cho.

c) Bóng đạt độ cao cực đại khi v = 0. Viết phương trình vận tốc của bóng theo công thức: \(v = {v_0} + at\). Giải phương trình ta tìm được thời điểm t.

d) Sử dụng công thức liên hệ giữa vận tốc, gia tốc và quãng đường: v² – v₀² = 2gh

e) Sử dụng công thức tính độ cao cực đại đối với chuyển động rơi tự do: H = \(\frac{1}{2}g{t^2}\)

Lời giải chi tiết:

a) Bóng được thả ra có vận tốc ban đầu bằng vận tốc của khinh khí cầu tại thời điểm bóng được thả, bóng chuyển động chậm dần đều lên theo khinh khí cầu. Sau đó, dưới tác dụng của trọng lực, bóng có vận tốc v = 0 và từ đó rơi tự do đến khi chạm đất.

b) Đồ thị vận tốc – thời gian của bóng được mô tả như hình vẽ:

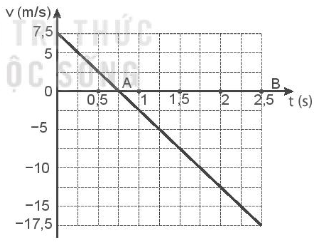
c) Chọn trục tọa độ Ox theo phương thẳng đứng, chiều dương hướng lên trên, gốc tại vị trí thả viên bóng, gốc thời gian t = 0 là lúc thả bóng.

Khí cầu đang bay lên với vận tốc 7,5m/s nên ban đầu hòn đá có vận tốc v₀ = 7,5m/s

Phương trình vận tốc của bóng:  v = v₀ + gt = 7,5 – 10t

Khi bóng đạt độ cao cực đại v = 0:

=> t = \(\frac{{ - 7,5}}{{ - 10}}\)= 0,75 s.

Vậy sau 0,75 s, bóng đạt độ cao cực đại.

Với v₀ = 5 m/s, a = - g = 9,8 m/s², x₀ = 0 nên x = 5t – 4,9t² (m)

Khi chạm đất: x = -300 m, ta có: 4,9t² - 5t – 300 = 0

d) Quãng đường đi được của bóng từ khi được thả ra tới khi đạt độ cao cực đại là:

Sử dụng công thức liên hệ giữa vận tốc, gia tốc và quãng đường: v² – v₀² = 2gh => h = -\(\frac{{v_0^2}}{{2g}}\)= 2,81 m.

e) Thời gian bóng rơi tự do từ độ cao cực đại tới đất: t’ = 2,5 – 0,75 = 1,75 s.

Khi đó độ cao cực đại của bóng cách mặt đất: H = \(\frac{{gt{'^2}}}{2}\)= 15,31 m.

---

II.8

Hình II.4 vẽ quỹ đạo của một quả cầu lông được đánh lên với vận tốc ban đầu v₀ = 10 m/s ở độ cao 2 m so với mặt đất. Bỏ qua sức cản của không khí và lấy g = 9,8 m/s².

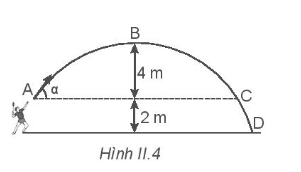
a) Xác định độ lớn của góc α.

b) Xác định vận tốc của quả cầu ở vị trí B.

c) Tính khoảng cách giữa vị trí rơi chạm đất của quả cầu và vị trí đứng của

người đánh cầu.

Phương pháp giải:

Chọn hệ trục tọa độ.

a) Vận dụng công thức: v_yB² – v_0y² = 2gh₁.

Khi đạt độ cao cực đại thì v_yB = 0. Chiếu v_0y lên hệ trục ta đươc:

=> -v₀²sin²α = 2gh₁ => sin\(\alpha \)=> α.

b) Tổng hợp vận tốc ta có: \(\overrightarrow {{v_B}}  = {\overrightarrow v _{xB}} + {\overrightarrow v _{yB}}\). Chiếu lên hệ tọa độ, thay số để tìm được v_B.

c) Khoảng cách giữa vị trí rơi chạm đất của quả cầu và vị trí đứng của người đánh cầu = tổng khoảng cách giữa vị trí người đánh cầu đến vị trí quả cầu đạt độ cao cực đại và vị trí quả cầu đạt độ cao cực đại đến khi quả cầu chạm đất:

L = L₁ + L₂ = v_xt₁ + v_xt₂.

Lời giải chi tiết:

Chọn hệ trục tọa độ Oxy có gốc tại vị trí quả cầu tiếp xúc với vợt và được đánh lên, chiều dương hướng lên trên (Oy) và từ trái sang phải (Ox), gốc thời gian t = 0 là lúc đánh quả cầu.

a) Khi đạt độ cao cực đại thì v_yB = 0.

v_yB² – v_0y² = 2gh₁ => -v₀²sin²α = 2gh₁

=> sinα = \(\sqrt {\frac{{2.9,8.4}}{{{{10}^2}}}} \)= 0,885 => α ≈ 62^o

b) Ta có chuyển động của quả cầu là tổng hợp của 2 loại chuyển động: chuyển động theo phương thẳng đứng và chuyển động theo phương nằm ngang.

Do đó, tổng hợp vận tốc của chuyển động, ta được:

\(\overrightarrow {{v_B}}  = {\overrightarrow v _{xB}} + {\overrightarrow v _{yB}}\)

=> v_B = v₀cosα + 0 ≈ 4,7 m/s.

c) L = L₁ + L₂ = v_xt₁ + v_xt₂ = v_x(t₁ + t₂).

Thời gian t₁ bằng thời gian để quả cầu chuyển động từ A tới B. Do đó:

t₁ = \(\sqrt {\frac{{2{h_1}}}{g}} \)= \(\sqrt {\frac{{2.4}}{{9,8}}} \)= 0,9

Thời gian t2 bằng thời gian để quả cầu rơi từ độ cao B tới mặt đất:t₂ = \(\sqrt {\frac{{2{h_2}}}{g}} \)= \(\sqrt {\frac{{2.(4 + 2)}}{{9,8}}} \)= 1,1 S.Do đó: L = 4,7.(0,9 + 1,1) = 9,4 m.

---

II.9

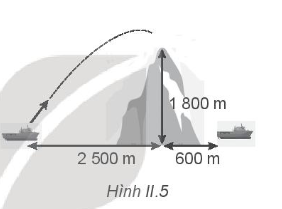
Một con tàu chiến ở bên này ngọn núi trên một hòn đảo, bắn một viên đạn với vận tốc ban đầu 250 m/s theo phương nghiêng góc 75° so với mặt nước biển tới đích là một con tàu khác nằm ở phía bên kia ngọn núi. Biết vị trí của hai con tàu và độ cao của ngọn núi được mô tả như Hình II.5. Hỏi viên đạn có qua được đỉnh núi không và có rơi trúng con tàu kia không?

Phương pháp giải:

Để xác định xem viên đạn có bay được qua đỉnh núi hay không, ta tính độ cao viên đạt đạt được tại vị trí đỉnh núi.

Viết phương trình chuyển động của viên đạn theo phương Ox, Oy:

x = v_0x.t; y = v_0y + \(\frac{1}{2}g{t^2}\).

Khoảng cách đến đỉnh núi = 2500 m => x = 2500 => Tìm ra t. Thế t vào y, ta tìm được độ cao mà viên đạn đạt được.

Để xác định viên đạn có rơi trúng con tàu kia không, ta xác định tầm bay xa của viên đạn bằng công thức: L = d_xmax = \(\frac{{v_0^2{{\sin }^2}\alpha }}{g}\)

Lời giải chi tiết:

Chọn hệ trục tọa độ Oxy như hình vẽ:

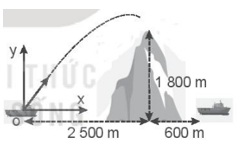
Ta có phương trình chuyển động của viên đạn:

Theo phương Ox:

x = v₀tcosα = (250.cos75^o).t

Theo phương Oy:

y = v₀tsinα - \(\frac{1}{2}\)gt² = (250.sin75^o)t - \(\frac{1}{2}\).10.t²

Để xác định xem viên đạn có bay qua được đỉnh núi hay không, ta thay x = 2500 = (250.cos75^o).t => t ≈ 38,64 s.

=> y = (250.sin75^o)t - \(\frac{1}{2}\).10.t² ≈ 1865,6 m. Vậy viên đạn bay qua được đỉnh núi.

Tầm bay xa của viên đạn: L = \(\frac{{v_0^2\sin 2\alpha }}{g}\)= \(\frac{{{{250}^2}.\sin ({{2.75}^o})}}{{10}}\)= 3125 m.

Viên đạn không bắn trúng tàu.