Bài 12. Chuyển động ném trang 19, 20, 21 SBT Vật lí 10 Kết nối tri thức với cuộc sống

12.1

Bi A có khối lượng lớn gấp 4 lần bi B. Tại cùng một lúc và ở cùng một độ cao, bi A được thả rơi còn bi B được ném theo phương nằm ngang. Nếu coi sức cản của không khí là không đáng kể thì

A. bi A rơi chạm đất trước bi B.

B. bi A rơi chạm đất sau bi B.

C. cả hai bi đều rơi chạm đất cùng một lúc với vận tốc bằng nhau.

D. cả hai bi đều rơi chạm đất cùng một lúc với vận tốc khác nhau.

Phương pháp giải:

Căn cứ vào đặc điểm của chuyển động ném ngang.

Lời giải chi tiết:

Chuyển động của vật bị ném ngang được phân tích thành 2 chuyển động thành phần là chuyển động theo phương thẳng đứng và chuyển động theo phương nằm ngang.

Trong đó:

+ Nếu bỏ qua sức cản không khí thì chuyển động thành phần theo phương thẳng đứng của vật là chuyển động rơi tự do với vận tốc ban đầu bằng 0. Do đó thời gian rơi của vật bị ném ngang chỉ phụ thuộc đồ cao h của vật bị ném, không phụ thuộc vận tốc ném. Nên nếu từ cùng một độ cao, đồng thời ném ngang các vật khác nhau với các vận tốc khác nhau thì chúng đều rơi xuống đất cùng một lúc.

+ Còn chuyển động thành phần theo phương nằm ngang là chuyển động thẳng đều với vận tốc v_x = v₀.

Vì vậy, bi A và bi B sẽ rơi chạm đất cùng lúc nhưng với vận tốc khác nhau.

Chọn đáp án D.

---

12.2

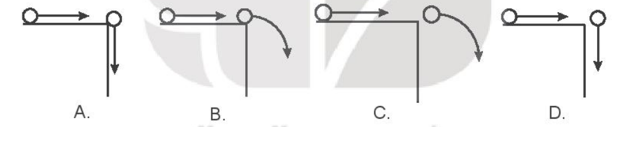
Một quả bóng đặt trên mặt bàn được truyền một vận tốc theo phương nằm ngang. Hình nào dưới đây mô tả đúng quỹ đạo của quả bóng khi rời khỏi mặt bàn?

Phương pháp giải:

Căn cứ vào đặc điểm của chuyển động ném ngang.

Lời giải chi tiết:

Chuyển động của vật bị ném ngang được phân tích thành 2 chuyển động thành phần là chuyển động theo phương thẳng đứng và chuyển động theo phương nằm ngang.

Trong đó:

+ Nếu bỏ qua sức cản không khí thì chuyển động thành phần theo phương thẳng đứng của vật là chuyển động rơi tự do với vận tốc ban đầu bằng 0.

+ Còn chuyển động thành phần theo phương nằm ngang là chuyển động thẳng đều với vận tốc v_x = v₀.

Do đó quỹ đạo của quả bóng được tổng hợp bởi cả 2 loại chuyển động.

A, D sai vì nó chỉ có một loại chuyển động là chuyển động nhanh dần đều theo phương thẳng đứng, chiều từ trên xuống.

C sai vì điểm rơi của quả bóng không tiếp xúc với mặt bàn.

Chọn đáp án B.

---

12.3

Một vật được ném từ độ cao H với vận tốc ban đầu v₀ theo phương nằm ngang. Nếu bỏ qua sức cản của không khí thì tầm xa L

A. tăng 4 lần khi v₀ tăng 2 lần.

B. tăng 2 lần khi H tăng 2 lần.

C. giảm 2 lần khi H giảm 4 lần.

D. giảm 2 lần khi v₀ giảm 4 lần. 

Phương pháp giải:

Áp dụng công thức tính tầm xa của vật bị ném: L = v₀\(\sqrt {\frac{{2H}}{g}} \)_.

Lời giải chi tiết:

A: Xét v₀ tăng 2 lần. Giả sử: v₀₂ = 2v₀₁.Ta có:

L₁ = v₀₁\(\sqrt {\frac{{2H}}{g}} \); L₂ = v₀₂\(\sqrt {\frac{{2H}}{g}} \)= 2v₀₁\(\sqrt {\frac{{2H}}{g}} \)= 2L₁ => L tăng 2 lần.

B: Xét H tăng 2 lần. Giả sử: H₂ = 2H₁. Ta có:

L₁ = v₀\(\sqrt {\frac{{2{H_1}}}{g}} \); L₂ = v₀\(\sqrt {\frac{{2{H_2}}}{g}} \)= v₀\(\sqrt {\frac{{2.2{H_1}}}{g}} \) = \(\sqrt 2 \)L₁ => L tăng \(\sqrt 2 \)lần.

C: Xét H giảm 4 lần. Giả sử: H₁ = 4H₂. Ta có:

L₁ = v₀\(\sqrt {\frac{{2{H_1}}}{g}} \)= v₀\(\sqrt {\frac{{2.4{H_2}}}{g}} \)= 2v₀\(\sqrt {\frac{{2{H_2}}}{g}} \); L₂ = v₀\(\sqrt {\frac{{2{H_2}}}{g}} \).

=> L₁ = 2L₂

=> L giảm 2 lần.

D: Xét v₀ giảm 4 lần. Giả sử: v₀₁ = 4v₀₂.Ta có:

L₁ = v₀₁\(\sqrt {\frac{{2H}}{g}} \) = 4v₀₂\(\sqrt {\frac{{2H}}{g}} \); L₂ = v₀₂\(\sqrt {\frac{{2H}}{g}} \).

=> L₁ = 4L₂ => L giảm 4 lần.

Chọn đáp án C.

---

12.4

Một viên đạn được bán theo phương nằm ngang từ một khẩu súng đặt ở độ cao 45,0 m so với mặt đất. Vận tốc của viên đạn khi vừa ra khỏi nòng súng có độ lớn là 250 m/s. Lấy g = 9,8 m/s.

a) Sau bao lâu thì viên đạn chạm đất?

b) Viên đạn rơi xuống đất cách điểm bắn theo phương nằm ngang bao

nhiêu mét?

c) Ngay trước khi chạm đất, vận tốc của viên đạn có độ lớn bằng bao nhiêu?

Phương pháp giải:

a) Sử dụng công thức tính thời gian rơi của vật bị ném ngang: t = \(\sqrt {\frac{{2h}}{g}} \).

b) Sử dụng công thức tính tầm xa L của chuyển động ném ngang:

L = d_xmax = v_xt = v₀t.

c) Sử dụng công thức tổng hợp vận tốc: v² = v_x² + v_y²

Trong đó: v_x = v₀; v_y = gt.

Lời giải chi tiết:

a) Thời gian rơi của viên đạn là: t = \(\sqrt {\frac{{2h}}{g}} \)= \(\sqrt {\frac{{2.45}}{{9,8}}} \)≈ 3,03 s.

b) Viên đạn rơi xuống đất cách điểm bắn theo phương nằm ngang:

L = d_xmax = v_xt = v₀t = 250.3,03 = 757,5 m.

c) Vận tốc của viên đạn ngay trước khi chạm đất là:

Ta có: v² = v_x² + v_y² => v = \(\sqrt {{v_x}^2 + {\rm{ }}{v_y}^2} \)

Mà v_x = v₀ = 250 m/s; v_y = gt = 9,8.3,03 ≈ 29,7 m/s.

Do đó: v = \(\sqrt {{{250}^2} + {\rm{ 29,}}{{\rm{7}}^2}} \)≈ 252 m/s.

---

12.5

Một vật được ném theo phương nằm ngang từ độ cao 4,9 m, có tầm xa trên

mặt đất L= 5 m. Lấy g= 9,8 m/s²

a) Tính vận tốc ban đầu.

b) Viết phương trình chuyển động và vẽ đồ thị độ dịch chuyền – thời gian.

c) Xác định vận tốc của vật ngay trước khi chạm đất.

Phương pháp giải:

a) Áp dụng công thức tính tầm xa của vật bị ném: L = v₀\(\sqrt {\frac{{2H}}{g}} \)_.

b) Xác định độ dịch chuyển theo phương thẳng đứng y và độ dịch chuyển theo phương nằm ngang x.

c) Sử dụng công thức tổng hợp vận tốc: v² = v_x² + v_y²

Trong đó: v_x = v₀; v_y = gt.

Lời giải chi tiết:

a) Theo công thức tính tầm xa của vật bị ném: L = v₀\(\sqrt {\frac{{2h}}{g}} \)

=> v₀ = L\(\sqrt {\frac{g}{{2h}}} \)= 5\(\sqrt {\frac{{9,8}}{{2.4,9}}} \)= 5 m/s.

b) Ta cần xác định được mối quan hệ giữa độ dịch chuyển theo phương thẳng đứng y và độ dịch chuyển theo phương nằm ngang x:

Ta có: x = v₀t => t = \(\frac{x}{{{v_0}}}\);

y = h = \(\frac{1}{2}\)gt² = 4,9 - \(\frac{1}{2}\)g\(\frac{{{x^2}}}{{v_0^2}}\)= 4,9 – 0,196x²

Ta lập bảng biến thiên với 6 giá trị của x và y:

x (m)	0	1	2	3	4	5
y (m)	4,9	4,7	4,1	3,1	1,8	0

 

Quỹ đạo là \(\frac{1}{2}\)đường parabol như hình vẽ:

 

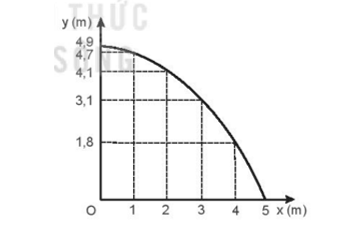
c) Ta có v_x = v₀ = 5 m/s;

v_y = gt = g\(\sqrt {\frac{{2h}}{g}} \)= \(\sqrt {2gh} \)= \(\sqrt {2.9,8.4,9} \)= 9,8 m/s.

Do đó: v =\(\sqrt {{v_x}^2 + {\rm{ }}{v_y}^2} \) =\(\sqrt {{5^2} + {\rm{ 9,}}{{\rm{8}}^2}} \)≈ 11m/s.

Ta có: tanα = \(\frac{{{v_y}}}{{{v_x}}}\)= 1,96 => α ≈ 63^o.

Vậy vận tốc của vật ngay trước khi chạm đất có độ lớn là 11 m/s, hướng xuống dưới 63^o so với phương nằm ngang.

---

12.6

Một máy bay đang bay theo phương nằm ngang ở độ cao 100 m với vận tốc 720 km/h. Muốn thả một vật trúng mục tiêu trên mặt đất thì phải thả khi máy bay còn cách mục tiêu theo phương nằm ngang là bao nhiêu mét?

Phương pháp giải:

Áp dụng công thức tính tầm xa của vật bị ném: L = v₀\(\sqrt {\frac{{2h}}{g}} \)_.

Lời giải chi tiết:

Nếu bỏ qua sức cản của không khí thì:

L = v₀\(\sqrt {\frac{{2h}}{g}} \)= 200\(\sqrt {\frac{{2.100}}{{9,8}}} \)≈ 903,5 m.

Thực tế, do có sức cản không khí nên L sẽ có giá trị nhỏ hơn 903,5 m.

Vậy cần thả vật khi máy bay còn cách mục tiêu theo phương nằm ngang nhỏ hơn 903,5 m.

---

12.7

Trong chuyển động của vật được ném xiên từ mặt đất thì đại lượng nào sau

đây không đổi?

A. Gia tốc của vật.

B. Độ cao của vật

C. Khoảng cách theo phương nằm ngang từ điểm vật được ném tới vật.

D. Vận tốc của vật.

Phương pháp giải:

Dựa vào đặc điểm của chuyển động ném xiên.

Lời giải chi tiết:

Trong các đại lượng trên chỉ có gia tốc của vật là không đổi và bằng gia tốc trọng trường g.

Chọn đáp án A.

---

12.8

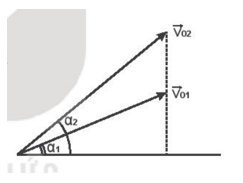
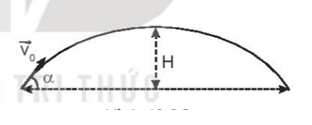
Hai vật được đồng thời ném từ mặt đất lên với vận tốc ban đầu vẽ như Hình 12.1. Nếu bỏ qua sức cản của không khí thì

A. vật 1 chạm đất trước.

B. hai vật chạm đất cùng một lúc.

C. hai vật có tầm bay cao như nhau.

D. vật 1 có tầm bay cao hơn.

Phương pháp giải:

Dựa vào công thức tính tầm bay cao của vật được ném xiên:

Tầm cao: H = d_ymax = \(\frac{{v_{0y}^2}}{{2g}}\)= \(\frac{{v_0^2.{{\sin }^2}\alpha }}{{2g}}\)

Lời giải chi tiết:

Ta có: Tầm cao H = d_ymax = \(\frac{{v_0^2.{{\sin }^2}\alpha }}{{2g}}\)

Từ Hình 12.1 ta thấy 0 < α₁ < α₂ < 90^o => 0 < sin α₁ < sinα₂ < 1.

Và v₀₁ < v₀₂

=> \(\frac{{v_{01}^2.{{\sin }^2}{\alpha _1}}}{{2g}}\) < \(\frac{{v_{02}^2.{{\sin }^2}{\alpha _2}}}{{2g}}\)=> H₁ < H₂.

A đúng, B sai vì vật 1 có tầm bay cao thấp hơn thì thời gian cần để chạm đất cũng nhỏ hơn vật 2.

C, D sai vì hai vật có tầm bay cao khác nhau và vật 1 có tầm bay cao thấp hơn.

Chọn đáp án A.

---

12.9

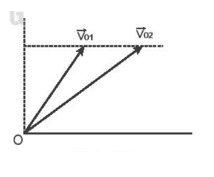
Hai vật được ném đồng thời ném từ mặt đất lên với vận tốc ban đầu như Hình 12.2. Nếu bỏ qua sức cản của không khí thì câu nào sau đây không đúng?

A. Hai vật chạm đất cùng một lúc.

B. Hai vật cùng có tầm bay xa.

C. Vật 2 có tầm bay xa lớn hơn.

D. Hai vật có cùng tầm bay cao.

Phương pháp giải:

Dựa vào công thức tính tầm bay cao và tầm bay xa của vật được ném xiên:

Tầm cao: H = d_ymax = \(\frac{{v_{0y}^2}}{{2g}}\) = \(\frac{{v_0^2.{{\sin }^2}\alpha }}{{2g}}\)

Tầm xa: L = d_xmax =  \(\frac{{v_{0x}^2}}{g}\) = \(\frac{{v_0^2.{{\sin }^2}2\alpha }}{g}\)

Lời giải chi tiết:

Ta có công thức tính tầm bay cao và tầm bay xa của vật được ném xiên như sau:

Tầm cao: H = d_ymax = \(\frac{{v_{0y}^2}}{{2g}}\) = \(\frac{{v_0^2.{{\sin }^2}\alpha }}{{2g}}\)

Tầm xa: L = d_xmax =  \(\frac{{v_{0x}^2}}{g}\) = \(\frac{{v_0^2.{{\sin }^2}2\alpha }}{g}\)

Từ Hình 12.2 chọn hệ tọa độ Oxy, gốc O như hình, chiều dương là chiều từ dưới lên (Oy) và từ trái sang phải (Ox). Khi đó ta có:

+ H₁ = \(\frac{{v_{01y}^2}}{{2g}}\); H₂ = \(\frac{{v_{02y}^2}}{{2g}}\)

Với v_01y = v_01x => H₁ = H₂.

+ L₁ = \(\frac{{v_{01x}^2}}{g}\); L₂ = \(\frac{{v_{02x}^2}}{g}\)

Với v_01x < v_02x => L₁ < L₂.

=> Hai vật có cùng tầm bay cao => Thời gian chạm đất của hai vật là như nhau.

=> Vật 2 có tầm bay xa lớn hơn.

Chọn đáp án B.

---

12.10

Một vật được ném xiên từ mặt đất với vận tốc ban đầu có độ lớn v₀ = 50 m/s. Khi lên tới điểm cao nhất, vận tốc của vật có độ lớn là 40 m/s. Bỏ qua sức cản của không khí, lấy g= 10 m/s².

a) Xác định góc ném α.

b) Vẽ quỹ đạo chuyển động của vật.

c) Tính tầm cao và tầm xa của vật.

Phương pháp giải:

a) Ta có v_x = v₀cosα => cosα = \(\frac{{{v_x}}}{{{v_{_0}}}}\). Từ đó suy ra góc ném α.

b) Quỹ đạo chuyển động của vật có dạng hình parabol với góc ném được xác định ở câu a).

c) Dựa vào công thức tính tầm bay cao và tầm bay xa của vật được ném xiên:

Tầm cao: H = d_ymax = \(\frac{{v_{0y}^2}}{{2g}}\) = \(\frac{{v_0^2.{{\sin }^2}\alpha }}{{2g}}\)

Tầm xa: L = d_xmax =  \(\frac{{v_{0x}^2}}{g}\) = \(\frac{{v_0^2.{{\sin }^2}2\alpha }}{g}\)

Lời giải chi tiết:

a) Tại điểm cao nhất thì vận tốc theo phương thẳng đứng v_y = 0.

=> v_x = \(\sqrt {{v^2} - v_y^2} \)= \(\sqrt {{{40}^2} - {0^2}} \)= 40 m/s.

Mà ta có v_x = v₀cosα => cosα = \(\frac{{{v_x}}}{{{v_{_0}}}}\)= \(\frac{{40}}{{50}}\)=> α ≈ 36,87^o.

b) Quỹ đạo chuyển động của vật có dạng hình parabol với góc ném được xác định ở câu a) như hình vẽ:

c) Ta có:

Tầm cao: H  = \(\frac{{v_0^2.{{\sin }^2}\alpha }}{{2g}}\)= 45 m.

Tầm xa: L= \(\frac{{v_0^2.{{\sin }^2}2\alpha }}{g}\)= 240 m.

---

12.11

Một cầu thủ bóng rổ cao 2m đứng cách xa rổ 10 m theo phương nằm ngang để tập ném bóng vào rổ. Biết miệng rổ ở độ cao 3,05 m. Hỏi người đó phải ném bóng từ độ cao ngang đầu với vận tốc theo phương 45° có độ lớn bằng bao nhiêu đề bóng rơi vào rổ? Lấy g= 9,8 m/s.

Phương pháp giải:

Viết phương trình độ dịch chuyển theo phương Ox và Oy:

d_x = v_0xt; d_y = v_0yt - \(\frac{1}{2}\)gt². Để bóng rơi trúng rổ thì d_x = 10 m, d_y = 1,05 m. Giải phương trình ta tìm được v₀.

Lời giải chi tiết:

Chọn hệ trục tọa độ Oxy như hình vẽ. Ta có:

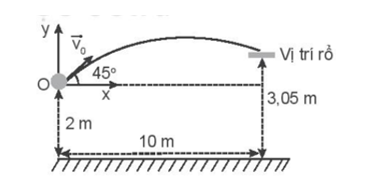
Theo phương Ox: d_x = v_0xt = v₀t.cos45^o = \(\frac{{\sqrt 2 }}{2}\)v₀t (m)_.

Theo phương Oy: d_y = v_0yt - \(\frac{1}{2}\)gt² = \(\frac{{\sqrt 2 }}{2}\)v₀t – 5t² (m).

Để bóng rơi trúng rổ thì d_x = 10 m, d_y = 1,05 m.

Khi đó: d_x = \(\frac{{\sqrt 2 }}{2}\)v₀t = 10 m => d_y = \(\frac{{\sqrt 2 }}{2}\)v₀t – 5t² = 10 – 5t² = 1,05 m.

=> t = \(\frac{{\sqrt {179} }}{{10}}\)s.

=> v₀ = \(\frac{{10.2}}{{\sqrt 2 .\frac{{\sqrt {179} }}{{10}}}}\)≈ 10,57 m/s.

---

12.12

Một diễn viên biểu diễn mô tô bay đang phóng xe trên mật dốc nằm nghiêng 30° để bay qua các ô tô như trong Hình 12.3. Biết vận tốc của xe mô tô khi rời khỏi đỉnh dốc là 14 m/s. Chiều cao của ô tô bằng chiều cao của dốc, Chiều dài của ô tô là 3,2 m. Lấy g = 10 m/s².

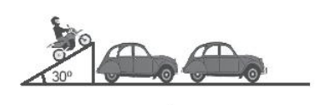
a) Tính thời gian từ khi xe rời đỉnh dốc tới khi đạt độ cao cực đại.

b) Mô tô có thể bay qua được nhiều nhất là bao nhiêu ô tô?

Phương pháp giải:

Chuyển động của mô tô bay được coi như chuyển động ném xiên góc 30^o so với phương nằm ngang, với vận tốc ban đầu v₀ = 14 m/s.

- Sử dụng công thức tính vận tốc: v_y = gt => t = \(\frac{{{v_y}}}{g}\).

- Sử dụng công thức tính tầm bay xa của vật: L = d_xmax =  \(\frac{{v_{0x}^2}}{g}\) = \(\frac{{v_0^2.{{\sin }^2}2\alpha }}{g}\)

Lời giải chi tiết:

Chuyển động của mô tô bay được coi như chuyển động ném xiên góc 30^o so với phương nằm ngang, với vận tốc ban đầu v₀ = 14 m/s.

a) Thời gian từ khi xe rời đỉnh dốc tới khi đạt đò cao cực đại là:

Ta có: v_y = gt => t = \(\frac{{{v_y}}}{g}\)= \(\frac{{{v_0}\sin \alpha }}{g}\)= \(\frac{{14\sin {{30}^o}}}{{10}}\)= 0,7 s.

b) Tầm xa của mô tô bay tính từ vị trí xe rời đỉnh dốc:

L = \(\frac{{v_0^2.{{\sin }^2}2\alpha }}{g}\) = \(\frac{{{{14}^2}{{\sin }^2}({{2.30}^o})}}{{10}}\)≈16,97 m.

Vì mỗi xe dài 3,2 m => mô tô có thể bay qua nhiều nhất 5 xe ô tô.

---

1

Hình 12.4 vẽ đồ thị vận tốc – thời gian và của chuyển động của một quả bóng được thả rơi không vận tốc ban đầu.

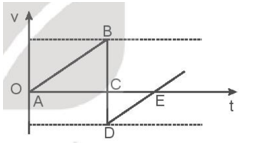
a) Hãy mô tả chuyển động của quả bóng từ A đến B và từ D đến E.

b) Tại sao độ dốc của đường AB bằng độ dốc của đường DE?

c) Độ lớn của diện tích hình ABC bằng độ lớn của đại lượng nào của chuyển động?

d) Tại sao diện tích hình ABC lớn hơn diện tích hình CDE?

Phương pháp giải:

Quan sát đặc điểm đồ thị để mô tả và giải thích.

Lời giải chi tiết:

a) Mô tả chuyển động của quả bóng:

- Từ A đến B: Tại A là vị trí bóng được thả rơi (v_A = 0), bóng chuyển động nhanh dần đều theo chiều từ trên xuống dưới và chạm đất tại B.

- Từ D đến E: Sau khi chạm đất, bóng đổi chiều chuyển động, rồi chuyển động chậm dần đều theo chiều từ dưới lên trên. Bóng đạt độ cao cực đại tại E (v_E = 0).

b) Vì trong quá trình bóng rơi xuống và bay lên thì nó có cùng gia tốc g, nên đồ thị vận tốc – thời gian của hai quá trình này có độ dốc như nhau.

c) Độ lớn của diện tích ABC bằng quãng đường chuyển động của quả bóng từ lúc bắt đầu thả rơi đến lúc nó chạm đất.

d) Vì độ lớn vận tốc của bóng ngay sau khi chạm đất nhỏ hơn độ lớn vận tốc của bóng ngay trước khi chạm đất, tức là đã có sự hao phí năng lượng trong quá trình bóng chạm đất, nên quãng đường chuyển động khi bóng rơi xuống (A đến B) lớn hơn quãng đường chuyển động khi bóng nảy lên (D đến E) dẫn tới diện tích hình ABC lớn hơn diện tích hình CDE.

---

2

Quả bóng được thả từ độ cao 1,2 m. Sau khi chạm đất, nó nảy lên tới độ

cao 0,8 m. Thời gian bóng tiếp xúc với mặt đất giữa B và D là 0,16 s (Vì thời gian này quá nhỏ nên trong hình vẽ đã bỏ qua). Coi sức cản của không khi là không đáng kể, lấy g = 10 m/s².

a) Tính vận tốc của quả bóng ngay trước khi tiếp đất và ngay sau khi nảy lên.

b) Tính gia tốc của quả bóng trong thời gian tiếp xúc với đất.

Phương pháp giải:

Áp dụng công thức tính vận tốc và gia tốc của chuyển dộng:

v =\(\sqrt {2gh} \); v = v₀ + at; v² – v₀² = 2as.

Lời giải chi tiết:

a)

Chọn trục tọa độ Ox theo phương thẳng đứng, chiều dương hướng xuống.

Vận tốc của quả bóng ngay trước khi tiếp đất:

v₁ = \(\sqrt {2g{h_1}} \)= \(\sqrt {2.1,2.10} \)= 4,9 m/s.

Do thời gian bóng tiếp xúc với đất là 0,16 s nên vận tốc của quả bóng ngay sau khi tiếp đất là:

v₂ = v₁ – gt = 4,9 – 10.0,16 = 3,3 m/s (vì khi chạm đất, đất là nguyên nhân làm cho quả bóng bị cản lại nên gia tốc a = -g).

b) Khi bóng bật lên đến độ cao 0,8 m (ngay tại độ cao đó vận tốc tức thời bằng v = 0)

Gia tốc của quả bóng trong thời gian tiếp xúc với đất là:

a = \(\frac{{v - {v_2}}}{{2{h_2}}}\)= \(\frac{{{0^2} - 3,{3^2}}}{{2.0,8}}\)≈ -6,8 m/s².

Độ lớn của gia tốc là 6,8 m/s², phương của gia tốc là phương thẳng đứng và có chiều ngược với chiều chuyển động.