Bài 21. Động lực học của chuyển động tròn. Lực hướng tâm trang 71, 72, 73 SBT Vật lí 10 Chân trời sáng tạo

21.1

Chuyển động của Trái Đất quanh Mặt Trời có thể xem như là chuyển động tròn đều vì

A. lực hấp dẫn giữa Trái Đất và Mặt Trời có độ lớn đáng kể.

B. lực hấp dẫn giữa Trái Đất và Mặt Trời có độ lớn rất nhỏ.

C. lực hấp dẫn giữa Trái Đất và Mặt Trời là lực hướng tâm, có độ lớn không đổi.

D. vecto vận tốc của Trái Đất luôn không đổi.

Phương pháp giải:

Vận dụng kiến thức về lực hướng tâm.

Lời giải chi tiết:

Chuyển động của Trái Đất quanh Mặt Trời có thể xem như là chuyển động tròn đều vì lực hấp dẫn giữa Trái Đất và Mặt Trời là lực hướng tâm, có độ lớn không đổi.

=> Chọn C

21.2

Để một vật có khối lượng bằng 12 kg chuyển động tròn đều trên quỹ đạo có bán kính 0,4 m với tốc độ 8 m/s thì lực hướng tâm phải có độ lớn gần nhất với giá trị nào sau đây?

A. 3,8.10³ N.               B. 9,6.10² N.              

C. 1,9.10³ N.               D. 3,8.10² N.

Phương pháp giải:

Vận dụng kiến thức về lực hướng tâm.

Lời giải chi tiết:

Tóm tắt:

m = 12 kg

R = 0,4 m

v = 8 m/s

F_ht =?

Lời giải:

Lực hướng tâm có độ lớn là:

\({F_{ht}} = m.\frac{{{v^2}}}{R} = 12.\frac{{{8^2}}}{{0,4}} = 1920N \approx 1,{9.10^3}N.\)

=> Chọn C

21.3

Một vật nặng có khối lượng 4 kg được buộc vào đầu một sợi dây dài L = 1,2 m. Người ta dùng một máy cơ để quay đầu còn lại của dây sao cho vật nặng chuyển động tròn đều. Biết lực căng dây tối đa để dây không đứt có giá trị bằng 300 N. Để dây không đứt, vật được phép quay với tốc độ tối đa là

A. 7,91 vòng/s.                        B. 1,26 vòng/s.           

C. 2,52 vòng/s.                        D. 1,58 vòng/s.

Phương pháp giải:

Vận dụng kiến thức về lực hướng tâm.

Lời giải chi tiết:

Tóm tắt:

m = 4 kg

L = 1,2 m

T = 300 N

\(\omega  = ?\)

Lời giải:

Lực căng dây đóng vai trò lực hướng tâm:

\(T = m.\frac{{{v^2}}}{R} = m.L.{\omega ^2} \Rightarrow \omega  = 7,91\,rad/s.\)

Từ đây, ta có: \(\omega  = 2\pi .n \Rightarrow n = 1,26\,v\`o ng/s.\)

=> Chọn B

21.4

Xét chuyển động của một con lắc đơn (Hình 21.1) gồm một vật nặng, kích thước nhỏ được treo vào đầu của một sợi dây mảnh, không dãn, có khối lượng không đáng kể. Đầu còn lại của dây treo vào một điểm cố định. Trong quá trình chuyển động của vật nặng trong một mặt phẳng thẳng đứng, tại vị trí nào ta có thể xem chuyển động của vật có tính chất tương đương chuyển động tròn đều?

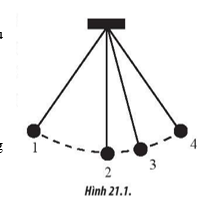
A. Vị trí 1.                               B. Vị trí 2.

C. Vị trí 3.                               D. Vị trí 4.

Phương pháp giải:

Vận dụng kiến thức về lực hướng tâm.

Lời giải chi tiết:

Tại vị trí 2, hợp lực \(m.\overrightarrow g  + \overrightarrow T \) có phương thẳng đứng, chiều hướng vào điểm treo, đóng vai trò lực hướng tâm.

=> Chọn B

21.1

Cho bán kính Trái Đất khoảng 6,37.10⁶ m và gia tốc trọng trường ở gần bề mặt Trái Đất là 9,8 m/s². Một vệ tinh chuyển động tròn đều gần bề mặt Trái Đất phải có tốc độ bằng bao nhiêu để không rơi xuống mặt đất?

Phương pháp giải:

Vận dụng kiến thức về lực hướng tâm.

Lời giải chi tiết:

Tóm tắt:

R = 6,37.10⁶ m

g = 9,8 m/s²

v =?

Lời giải:

Trọng lực tác dụng lên vệ tinh là lực hướng tâm:

\(m.g = m\frac{{{v^2}}}{R} \Rightarrow v = 7,{9.10^3}m/s = 7,9km/s.\)

21.2

Mặt Trăng quay quanh Trái Đất một vòng mất 27,3 ngày. Biết lực hấp dẫn giữa các vật có khối lượng được tính theo công thức: \({F_{hd}} = G.\frac{{{m_1}.{m_2}}}{{{r^2}}}\)

Với G = 6,67.10^-11 N.kg^-2.m² là hằng số hấp dẫn, m₁ và m₂ lần lượt là khối lượng của hai vật và r là khoảng cách giữa hai khối tâm của chúng.

Biết khối lượng của Trái Đất khoảng 5,97.10²⁴ kg. Hãy tính khoảng cách giữa tâm của Trái Đất và Mặt Trăng.

Phương pháp giải:

Vận dụng kiến thức về lực hấp dẫn.

Lời giải chi tiết:

Lực hấp dẫn giữa Mặt Trăng (khối lượng m) và Trái Đất (khối lượng M) là lực hướng tâm:

\(G.\frac{{m.M}}{{{r^2}}} = m.\frac{{{v^2}}}{r} \Rightarrow r = \sqrt[3]{{G.\frac{M}{{{{\left( {2\pi /T} \right)}^2}}}}} \approx 3,{83.10^8}m.\)

21.3

Một vật nặng có khối lượng bằng 5 kg được buộc vào một dây dài 0,8 m và thả cho chuyển động trong mặt phẳng thẳng đứng như Hình 21.2. Khi qua vị trí cân bằng O, vật có tốc độ 2,8 m/s. Tính gia tốc hướng tâm và lực căng dây khi vật đi qua vị trí cân bằng O. Lấy g = 9,8 m/s².

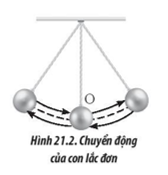
Phương pháp giải:

Vận dụng kiến thức về lực hướng tâm.

Lời giải chi tiết:

Tại vị trí cân bằng 0: \({a_{ht}} = \frac{{{v^2}}}{l} = 9,8m/{s^2}.\)

\(T = m.g + m.\frac{{{v^2}}}{l} = 98N.\)

21.4

Một chiếc xe đua có khối lượng 800 kg chạy với tốc độ lớn nhất (mà không bị trượt) theo đường tròn nằm ngang có bán kính 80 m (Hình 21.3) được một vòng sau khoảng thời gian 28,4 s. Tính:

a) gia tốc hướng tâm của xe.

b) hệ số ma sát nghỉ giữa các bánh xe và mặt đường. Lấy g = 9,8 m/s².

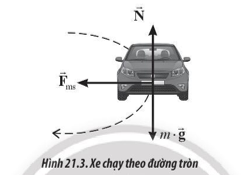
Phương pháp giải:

Vận dụng kiến thức về gia tốc hướng tâm.

Lời giải chi tiết:

a) \(v = \frac{{2\pi R}}{T} \approx 17,7m/s;\,{a_{ht}} = \frac{{{v^2}}}{R} \approx 3,92m/{s^2}.\)

b) Vì tốc độ xe lớn nhất nên lực ma sát nghỉ (đóng vai trò lực hướng tâm) có giá trị lớn nhất:

\({F_{ms}} = \mu .N = \mu .m.g = m.{a_{ht}} \Rightarrow \mu  = \frac{{{a_{ht}}}}{g} = 0,4.\)

21.5

Một vệ tinh địa tĩnh (là vệ tĩnh có vị trí tương đối không đổi đối với một vị trí trên Trái Đất) chuyển động quanh Trái Đất với lực hướng tâm là lực hấp dẫn giữa Trái Đất và vệ tinh (công thức được cho trong Bài 21.2). Biết gia tốc trọng trường tại mặt đất được tính theo biểu thức:                       \(g = G.\frac{M}{{{R^2}}}\)

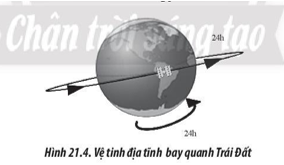
Với G = 6,67.10^-11 N.kg^-2.m² là hằng số hấp dẫn, M và R lần lượt là khối lượng và bán kính Trái Đất. Lấy gia tốc trọng trường tại mặt đất bằng 9,8 m/s² và bán kính Trái Đất khoảng 6,4.10⁶ m. Tính:

a) bán kính quỹ đạo của vệ tinh.

b) tốc độ của vệ tinh trên quỹ đạo.

Phương pháp giải:

Vận dụng kiến thức về lực hấp dẫn.

Lời giải chi tiết:

a) Chu kì của vệ tinh cũng là chu kì của Trái Đất:

\(G.\frac{{m.M}}{{{r^2}}} = m.\frac{{{v^2}}}{r} \Rightarrow G.\frac{{m.M}}{{{r^2}}} = \frac{{m.4{\pi ^2}.r}}{{{T^2}}}.\)

Suy ra: \({r^3} = G.\frac{M}{{4{\pi ^2}}}.{T^2} = g.\frac{{{T^2}.{R^2}}}{{4{\pi ^2}}} \Rightarrow r = 4,{22.10^7}m.\)

b) \(v = \frac{{2\pi r}}{T} = 3,{07.10^3}m/s.\)