Bài 20. Động học của chuyển động tròn trang 68, 69, 70 SBT Vật lí 10 Chân trời sáng tạo

20.1

Để chuyển đổi đơn vị số đo một góc từ rad (radian) sang độ và ngược lại, từ độ sang rad, hệ thức nào sau đây không đúng?

A. \({\alpha ^0} = \frac{{{{180}^0}}}{\pi }.\alpha \,rad\)                                      

B. \({60^0} = \frac{{{{180}^0}}}{\pi }.\frac{\pi }{3}rad\)

C. \({45^0} = \frac{{{{180}^0}}}{\pi }.\frac{\pi }{8}rad\)                                   

D. \(\frac{\pi }{2}rad = \frac{{{{180}^0}}}{\pi }.\frac{\pi }{2}\)

Phương pháp giải:

Vận dụng kiến thức về định nghĩa radian: \(1rad = \frac{{{{180}^0}}}{\pi } \approx 57,{2958^0}\).

Lời giải chi tiết:

Đáp án sai: C vì \({45^0} = \frac{{{{180}^0}}}{\pi }.\frac{\pi }{4}rad\).

=> Chọn C

20.2

Xét một cung tròn chắn bởi góc ở tâm bằng 1,8 rad. Bán kính đường tròn này bằng 2,4 cm. Chiều dài của cung tròn này và diện tích của hình quạt giới hạn bởi cung tròn này có độ lớn lần lượt bằng

A. 2,16 cm và 5,18 cm².                                 B. 4,32 cm và 10,4 cm².

C. 2,32 cm và 5,18 cm².                                  D. 4,32 cm và 5,18 cm².2

Phương pháp giải:

Vận dụng kiến thức về chiều dài cung tròn:

Khi góc chắn cung có số đo là \(\alpha \) (radian) thì chiều dài cung tròn sẽ bằng: \(s = {\alpha _{\left( {radian} \right)}}.R\).

Lời giải chi tiết:

Chiều dài cung tròn: 1,8.2,4 = 4,32 cm.

Diện tích phần hình quạt: \(\frac{1}{2}.2,{4^2}.1,8 \approx 5,18c{m^2}.\)

=> Chọn D

20.3

Một chất điểm M thực hiện chuyển động tròn đều như Hình 20.1.

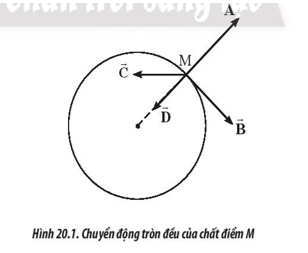
Nhận xét nào sau đây là đúng?

A. \(\overrightarrow A \) là vecto vận tốc, \(\overrightarrow B \) là vecto gia tốc.                                    

B. \(\overrightarrow B \) là vecto vận tốc, \(\overrightarrow A \) là vecto gia tốc.

C. \(\overrightarrow B \) là vecto vận tốc, \(\overrightarrow D \) là vecto gia tốc.

D. \(\overrightarrow C \) là vecto vận tốc, \(\overrightarrow D \) là vecto gia tốc.

Phương pháp giải:

Vận dụng kiến thức về vecto vận tốc và gia tốc trong chuyển động tròn.

Lời giải chi tiết:

Vận tốc trong chuyển động tròn đều có:

- Phương: Tiếp tuyến với quỹ đạo (đường tròn).

- Chiều: Theo chiều chuyển động.

- Độ lớn: Không đổi, bằng \(v = \omega .R\).

=> \(\overrightarrow B \) là vecto vận tốc.

Gia tốc trong chuyển động tròn đều có đặc điểm:

- Phương: Trùng với bán kính

- Chiều: Hướng vào tâm của vòng tròn quỹ đạo (nên có tên là gia tốc hướng tâm)

- Độ lớn: Không đổi và bằng: \({a_{ht}} = \frac{{{v^2}}}{R} = {\omega ^2}.R\)

=> \(\overrightarrow D \) là vecto gia tốc.

=> Chọn C

20.4

Chuyển động nào sau đây có thể xem như là chuyển động tròn đều?

A. Chuyển động của một vật được ném xiên từ mặt đất.

B. Chuyển động trong mặt phẳng thẳng đứng của một vật được buộc vào một dây có chiều dài cố định.

C. Chuyển động của một vệ tinh nhân tạo có vị trí tương đối không đổi đối với một điểm trên mặt đất (vệ tinh địa tĩnh).

D. Chuyển động của một quả táo khi rời ra khỏi cành cây.

Phương pháp giải:

Vận dụng kiến thức về chuyển động tròn đều.

Lời giải chi tiết:

Vì va chạm đàn hồi có những đặc điểm sau: động lượng và động năng của hệ được bảo toàn. Trước va chạm, động năng của hệ khác không. Do đó, sau va chạm, động năng của hệ cũng phải khác không.

=> Chọn C

20.1

Điền vào chỗ trống của bảng dưới đây các độ lớn của các góc theo độ hoặc radian (rad):

Phương pháp giải:

Vận dụng kiến thức về định nghĩa radian: \(1rad = \frac{{{{180}^0}}}{\pi } \approx 57,{2958^0}\).

Lời giải chi tiết:

20.2

Trong mô hình cổ điển Bohr của nguyên tử hydrogen, electron xem như chuyển động tròn đều quanh hạt nhân là proton với quỹ đạo có bán kính 0,529.10^-10 m với tốc độ 2,2.10⁶ m/s. Gia tốc hướng tâm của electron có độ lớn bằng bao nhiêu?

Phương pháp giải:

Vận dụng kiến thức về gia tốc hướng tâm trong chuyển động tròn đều.

Lời giải chi tiết:

\({a_{ht}} = \frac{{{v^2}}}{R} = 9,{15.10^{22}}m/{s^2}.\)

20.3

Một mô tơ điện quay quanh trục với tốc độ 3600 rpm (revolutions/min: vòng/phút). Tốc độ góc của mô tơ này bằng bao nhiêu?

Phương pháp giải:

Vận dụng kiến thức về tốc độ góc trong chuyển động tròn đều.

Lời giải chi tiết:

\(\omega  = \frac{{2\pi .3600}}{{60}} = 120\pi rad/s \approx 377rad/s.\)

20.4

Chuyển động của Mặt Trăng quanh Trái Đất được xem gần đúng là chuyển động tròn đều. Thời gian Mặt Trăng quay một vòng quanh Trái Đất khoảng 27,3 ngày. Khoảng cách trung bình từ tâm của Trái Đất đến Mặt Trăng là 385.10³ km. Hãy xác định:

a) tốc độ của Mặt Trăng (theo đơn vị km/h và m/s) và quãng đường Mặt Trăng chuyển động sau một ngày.

b) gia tốc hướng tâm của Mặt Trăng (theo đơn vị m/s²).

Phương pháp giải:

Vận dụng kiến thức về gia tốc và vận tốc trong chuyển động tròn đều.

Lời giải chi tiết:

a) \(v = \omega .R \approx 3,{69.10^3}km/h \approx 1,{03.10^3}m/s.\)

\(s = v.t \approx 3,{69.10^3}.24 \approx 88,{6.10^3}km.\)

b) \({a_{ht}} = \frac{{{v^2}}}{R} \approx 2,{76.10^{ - 3}}m/{s^2}.\)

20.5

Một chiếc xe chuyển động theo hình vòng cung với tốc độ 36 km/h và gia tốc hướng tâm 4,0 m/s2²²². Giả sử xe chuyển động tròn đều. Hãy xác định:

a) bán kính đường vòng cung.

b) góc quét bởi bán kính quỹ đạo (theo rad và độ) sau thời gian 3 s.

Phương pháp giải:

Vận dụng kiến thức về góc quét và bán kính trong chuyển động tròn đều.

Lời giải chi tiết:

a) \(R = \frac{{{v^2}}}{{{a_{ht}}}} = 25m.\)

b) \(\alpha  = \omega .\Delta t = 1,2rad \approx 68,{8^0}.\)

20.6

Một trái bóng được buộc vào một sợi dây và quay tròn đều trong mặt phẳng ngang như Hình 20.2. Trái bóng quay một vòng trong 1 s với tốc độ 0,5 m/s. Tính bán kính quỹ đạo và chiều dài L của sợi dây, biết góc hợp bởi dây và phương thẳng đứng bằng 30⁰.

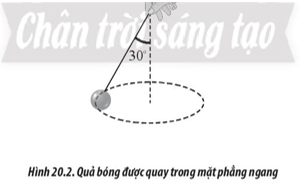
Phương pháp giải:

Vận dụng kiến thức về tốc độ góc trong chuyển động tròn đều.

Lời giải chi tiết:

\(\omega  = \frac{{2\pi }}{l} = \frac{{0,5}}{R} \Rightarrow R \approx 0,08m;L = \frac{R}{{\sin {{30}^0}}} = 0,16m.\)