Phần câu hỏi bài 9 trang 55 Vở bài tập toán 7 tập 2

Câu 25.

Khoanh tròn vào số là nghiệm của đa thức

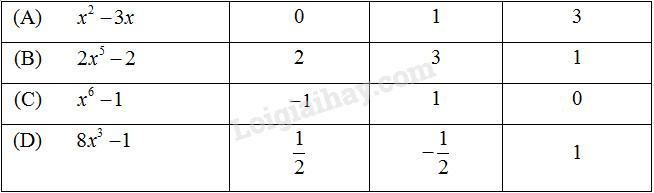
Phương pháp giải :

Ta lần lượt thay các giá trị \(x=x_o\) vào đa thức đã cho, nếu kết quả giá trị của đa thức bằng \(0\) thì \(x_o\) là nghiệm của đa thức đã cho.

Cách giải:

Thay \(x=0\) vào đa thức \(x^2-3x\) ta được:

\({0^2} - 3.0 = 0\)

Vậy \(x=0\) là nghiệm của đa thức \(x^2-3x\).

Thay \(x=3\) vào đa thức \(x^2-3x\) ta được:

\({3^2} - 3.3 = 9 - 9 = 0\)

Vậy \(x=3\) là nghiệm của đa thức \(x^2-3x\).

Thay \(x=1\) vào đa thức \(2{x^5} - 2\) ta được:

\({2.1^5} - 2 = 2 - 2 = 0\)

Vậy \(x=1\) là nghiệm của đa thức \(2{x^5} - 2\).

Thay \(x=-1\) vào đa thức \({x^6} - 1\) ta được:

 \({\left( { - 1} \right)^6} - 1 = 1 - 1 = 0\)

Vậy \(x=-1\) là nghiệm của đa thức \({x^6} - 1\).

Thay \(x=1\) vào đa thức \({x^6} - 1\) ta được:

 \({1^6} - 1 = 1 - 1 = 0\)

Vậy \(x=1\) là nghiệm của đa thức \({x^6} - 1\).

Thay \(x=\dfrac{1}{2}\) vào đa thức \(8{x^3} - 1\) ta được:

\(8.{\left( {\dfrac{1}{2}} \right)^3} - 1 = 8.\dfrac{1}{8} - 1 = 0\)

Vậy \(x=\dfrac{1}{2}\) là nghiệm của đa thức \(8{x^3} - 1\).

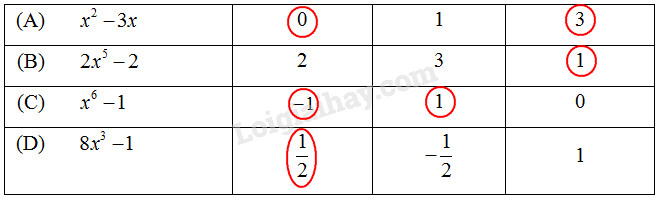
Ta điền vào bảng như sau:

---

Câu 26.

Khoanh tròn vào chữ cái trước khẳng định đúng.

(A) Đa thức \({x^2} - 5x + 6\) có các nghiệm là \(x = 2 ; x = 3\);

(B)  Đa thức \(3{x^2} - x\) có các nghiệm là \(x = 3;x = 0;\)

(C)  Đa thức \(2{x^2} - 2x + 1\) có vô số nghiệm;

(D) Đa thức \({x^3} - 3{x^2} + 2x\) có các nghiệm là \(x = 2; x = 0; x = 3\).

Phương pháp giải :

Vận dụng kiến thức: Nếu tại \(x=a\), đa thức \(P(x)\) có giá trị bằng \(0\) thì ta nói \(a\) (hoặc \(x=a\)) là một nghiệm của đa thức đó.

Cách giải :

(A) Đúng.

Thay \(x=2\) vào đa thức \({x^2} - 5x + 6\) ta được:

\({2^2} - 5.2 + 6 = 4 - 10 + 6 = 0\)

Thay \(x=3\) vào đa thức \({x^2} - 5x + 6\) ta được:

\({3^2} - 5.3 + 6 = 9 - 15 + 6 = 0\)

Vậy đa thức \({x^2} - 5x + 6\) có các nghiệm là \(x = 2 ; x = 3\).

(B) Sai, vì \(x=3\) không phải là nghiệm của đa thức.

Thay \(x=3\) vào đa thức \(3{x^2} - x\) ta được:

\({3.3^2} - 3 = 24\)

Vậy \(x=3\) không phải là nghiệm của đa thức \(3{x^2} - x\).

(C) Sai, vì \(1\) không là nghiệm của đa thức \(2{x^2} - 2x + 1\).

Thay \(x=1\) vào đa thức \(2{x^2} - 2x + 1\) ta được:

\({2.1^2} - 2.1 + 1 = 2 - 2 + 1 = 1\)

Vậy \(x=1\) không là nghiệm của đa thức \(2{x^2} - 2x + 1\), hay đa thức \(2{x^2} - 2x + 1\) không vô số nghiệm.

(D) Sai, vì \(x=3\) không phải là nghiệm của đa thức.

Thay \(x=3\) vào đa thức \({x^3} - 3{x^2} + 2x\) ta được:

\({3^3} - {3.3^2} + 2.3 = 6\)

Vậy \(x=3\) không là nghiệm của đa thức \({x^3} - 3{x^2} + 2x\).

Chọn (A).

---

Câu 27.

Điền vào chỗ trống để được khẳng định đúng.

(A) Đa thức \({x^2} - ....x\) có các nghiệm là \(x = 2; x = 0\);

(B) Đa thức \({x^2} + 6\) ………. nghiệm.

(C) Nếu đa thức \(a\,{x^2} + bx + c\) có nghiệm \(x = -1\) thì \(a – b + c = ………\);

(D) Đa thức \({x^3} - {x^2} - x + 1\) có các nghiệm là \(x = ……; x = 1\).

Phương pháp giải :

Vận dụng kiến thức: Nếu tại \(x=a\), đa thức \(P(x)\) có giá trị bằng \(0\) thì ta nói \(a\) (hoặc \(x=a\)) là một nghiệm của đa thức đó.

Cách giải :

(A) Đa thức \({x^2} - 2x\) có các nghiệm là \(x = 2; x = 0\);

Giải thích: Thay \(x=2\) vào đa thức \({x^2} - 2x\) ta được:

\({2^2} - 2.2 = 4 - 4 = 0\)

Vậy \(x=2\) là nghiệm của đa thức \({x^2} - 2x\).

(B) Đa thức \({x^2} + 6\) vô nghiệm.

Giải thích: \({x^2} \ge 0\) với mọi \(x\) nên \({x^2} + 6>0\) với mọi \(x\) hay đa thức \({x^2} + 6\) vô nghiệm.

(C) Nếu đa thức \(a\,{x^2} + bx + c\) có nghiệm \(x = -1\) thì \(a – b + c = 0\);

Giải thích: Đa thức \(a\,{x^2} + bx + c\) có nghiệm \(x = -1\) thì \(a.{\left( { - 1} \right)^2} + b.\left( { - 1} \right) + c = 0\) hay \(a – b + c = 0\).

(D) Đa thức \({x^3} - {x^2} - x + 1\) có các nghiệm là \(x = -1; x = 1\).

Giải thích: Thay \(x=-1\) vào đa thức \({x^3} - {x^2} - x + 1\) ta được:

\({1^3} - {1^2} - 1 + 1 = 1 - 1 - 1 + 1 = 0\)

Vậy \(x=-1\) là nghiệm của đa thức \({x^3} - {x^2} - x + 1\).