Phần câu hỏi bài 9 trang 39 Vở bài tập toán 6 tập 2

Câu 25

Nối mỗi dòng ở cột bên trái với một dòng ở cột bên phải để được khẳng định đúng :

Phương pháp giải:

Vận dụng định nghĩa : Hai số gọi là đối nhau nếu tổng của chúng bằng \(0\).

Lời giải chi tiết:

(A) Số đối của \(\dfrac{{ - 3}}{4}\) là \(\dfrac{3}{4}\) (A nối với 3)

(B) Số đối của \(\dfrac{{ - 7}}{9}\) là \(\dfrac{7}{9}\) (B nối với 1)

(C) Số đối của \(\dfrac{8}{3}\) là \( - \dfrac{8}{3}\) (C nối với 5)

(D) Số đối của \(0\) là \(0\) (D nối với 2).

Câu 26

Điền phân số thích hợp vào ô vuông :

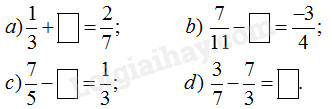
Phương pháp giải:

- Nhẩm lại quy tắc chuyển vế.

- Quy tắc trừ phân số : Muốn trừ một phân số cho một phân số, ta cộng số bị trừ với số đối của số trừ.

Lời giải chi tiết:

a) Vì \(\dfrac{2}{7} - \dfrac{1}{3} = \dfrac{2}{7} + \left( { - \dfrac{1}{3}} \right)\)\( = \dfrac{{6 + \left( { - 7} \right)}}{{21}}\)\( = \dfrac{{ - 1}}{{21}}\) nên điền vào ô trống phân số \(\dfrac{{ - 1}}{{21}}.\)

b) Vì \(\dfrac{7}{{11}} - \dfrac{{ - 3}}{4} = \dfrac{7}{{11}} + \dfrac{3}{4}\)\( = \dfrac{{28 + 33}}{{44}} = \dfrac{{61}}{{44}}\) nên cần điền vào ô trống phân số \(\dfrac{{61}}{{44}}.\)

c) Vì \(\dfrac{7}{5} - \dfrac{1}{3} = \dfrac{7}{5} + \dfrac{{ - 1}}{3} = \dfrac{{21 + \left( { - 5} \right)}}{{15}}\)\( = \dfrac{{16}}{{15}}\) nên cần điền vào ô trống phân số \(\dfrac{{16}}{{15}}.\)

d) Vì \(\dfrac{3}{7} - \dfrac{7}{3} = \dfrac{3}{7} + \dfrac{{ - 7}}{3} = \dfrac{{9 + \left( { - 49} \right)}}{{21}}\)\( = \dfrac{{ - 40}}{{21}}\) nên cần điền vào ô trống phân số \(\dfrac{{ - 40}}{{21}}.\)  

Câu 27

Kết quả của phép tính \(\dfrac{1}{2} + \dfrac{1}{{ - 3}} + \dfrac{1}{4} - \dfrac{{ - 1}}{5}\) là :

(A) \(\dfrac{{37}}{{60}};\)            (B) \(\dfrac{{13}}{{60}};\)

(C)\(\dfrac{{53}}{{60}};\)             (D) \(\dfrac{{77}}{{60}}.\)

Phương pháp giải:

Thực hiện các phép tính theo thứ tự từ trái sang phải.

Lời giải chi tiết:

\(\begin{array}{l}\dfrac{1}{2} + \dfrac{1}{{ - 3}} + \dfrac{1}{4} - \dfrac{{ - 1}}{5}\\ = \dfrac{{3 + \left( { - 2} \right)}}{6} + \dfrac{1}{4} - \dfrac{{ - 1}}{5}\\ = \dfrac{1}{6} + \dfrac{1}{4} - \dfrac{{ - 1}}{5}\\ = \dfrac{{2 + 3}}{{12}} - \dfrac{{ - 1}}{5}\\ = \dfrac{5}{{12}} - \dfrac{{ - 1}}{5}\\ = \dfrac{5}{{12}} + \dfrac{1}{5}\\ = \dfrac{{25 + 12}}{{60}}\\ = \dfrac{{37}}{{60}}\end{array}\)

Chọn (A)