Phần câu hỏi bài 9 trang 101 Vở bài tập toán 8 tập 2

Câu 19a

a) Cho hình vẽ 48. Hãy viết các cặp tam giác đồng dạng (theo đúng thứ tự các đỉnh tương ứng) vào chỗ trống:

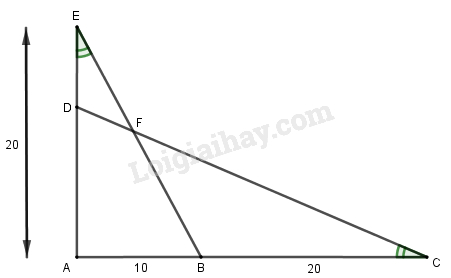
\(\begin{array}{l}{a_1})\,\Delta ....... \backsim \Delta .......\\{a_2})\,\Delta ....... \backsim \Delta .......\end{array}\) 

Phương pháp giải:

Sử dụng trường hợp đồng dạng thứ ba: Hai tam giác có hai cặp góc tương ứng bằng nhau thì đồng dạng với nhau.

Giải chi tiết:

Xét tam giác \(ABE\) và tam giác \(ADC\) có: 

Chung \(\widehat A\)

\(\widehat {AEB} = \widehat {ACD}\left( {gt} \right)\)

\( \Rightarrow \Delta ABE \backsim \Delta ADC\left( {g.g} \right)\)

Xét tam giác \(DEF\) và tam giác \(BCF\) có:

\(\widehat {DEF} = \widehat {BCF}\left( {gt} \right)\)

\(\widehat {DFE} = \widehat {BFC}\) (hai góc đối đỉnh)

Suy ra \(\Delta DEF \backsim \Delta BCF\left( {g.g} \right)\)

Vậy ta điền như sau:

\(\begin{array}{l}{a_1})\,\Delta ABE \backsim \Delta ADC\\{a_2})\,\Delta DEF \backsim \Delta BCF\end{array}\)

Câu 19b

b) Cho biết \(AB = 10,BC = 20,AE = 20\).

\({b_1})\) Độ dài của đoạn thẳng \(DE\) là:

A. \(5\)                             B. \(6,5\)

C. \(5,5\)                          D. \(7\)

Khoanh tròn vào chữ cái trước khẳng định đúng. 

Phương pháp giải:

Sử dụng kết quả câu a, từ hai tam giác đồng dạng suy ra các tỉ số đồng dạng và tính toán.

Giải chi tiết:

Theo câu a) \(\Delta ABE \backsim \Delta ADC\)\( \Rightarrow \dfrac{{AB}}{{AD}} = \dfrac{{AE}}{{AC}}\) \( \Rightarrow \dfrac{{10}}{{AD}} = \dfrac{{20}}{{10 + 20}}\) \( \Rightarrow AD = \dfrac{{10.30}}{{20}} = 15\)

Suy ra \(DE = AE - AD\) \( = 20 - 15 = 5\).

Chọn A.

\({b_2})\) (Tính chính xác đến hai chữ số thập phân). Độ dài của đoạn thẳng \(CD\) là:

A. \(30,25\)                          B. \(35,45\)

C. \(33,54\)                          D. \(32,25\)

Khoanh tròn vào chữ cái trước khẳng định đúng.

Phương pháp:

Sử dụng định lí Pi – ta – go trong tam giác vuông.

Cách giải:

Tam giác \(ACD\) vuông tại \(A\) nên \(A{C^2} + A{D^2} = C{D^2}\)

\( \Rightarrow {\left( {10 + 20} \right)^2} + {15^2} = C{D^2}\) \( \Rightarrow C{D^2} = 1125 \Rightarrow CD \approx 33,54\).

Chọn C. 

\({b_3})\) Cho biết độ dài của đoạn \(CF = 29,8\). Độ dài của đoạn thẳng \(EF\) là:

A. \(7,45\)                             B. \(7,55\)

C. \(7,65\)                             D. \(7,75\)

Khoanh tròn vào chữ cái trước khẳng định đúng.

Phương pháp:

Sử dụng kết quả câu a), từ hai tam giác đồng dạng suy ra các tỉ số và tính toán.

Cách giải:

Từ câu a) ta có \(\Delta DEF \backsim \Delta BCF\)\( \Rightarrow \dfrac{{DE}}{{BC}} = \dfrac{{EF}}{{CF}} \Rightarrow \dfrac{5}{{20}} = \dfrac{{EF}}{{29,8}}\) \( \Rightarrow EF = \dfrac{{5.29,8}}{{20}} = 7,45\)

Chọn A.