Bài 42 trang 102 Vở bài tập toán 8 tập 2

Đề bài

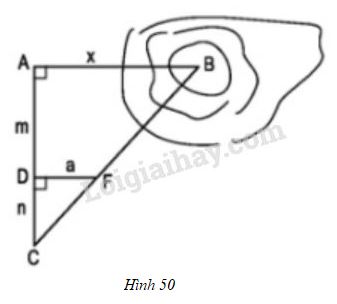
Để đo khoảng cách giữa hai điểm \(A\) và \(B\), trong đó \(B\) không tới được, người ta tiến hành đo và tính khoảng cách như hình 57:

\(AB // DF; AD = m; DC = n; DF = a\).

a) Em hãy nói rõ về cách đo như thế nào.

b) Tính độ dài \(x\) của khoảng cách \(AB\).

Lời giải chi tiết

Bài toán này được đo bằng hai dụng cụ đơn giản là ê ke và thước đo độ dài. Cách đo như sau:

+ Ở một vị trí \(A\) bất kì (có thể tới được), dùng hai cạnh góc vuông của ê ke để xác định góc vuông hợp bởi hai tia \(AB\) và \(AC\). Tia \(AC\) có thể dùng dây để xác định vị trí trên mặt đất.

+ Ở vị trí \(D\) trên tia \(AC\), dựng đoạn \(DF\) vuông góc với \(AC\) bằng cách dung ê ke đo góc \(FDC = {90^0}\)

+ Ngắm nhìn \(BF\) cắt tia \(AD\) tại \(C\) (ba điểm \(B,F,C\) thẳng hàng)

+ Đo độ dài \(AD = m,DC = n,DF = a\)

b) Tính độ dài \(x\) của khoảng cách \(AB\).

\(\Delta ABC\) và \(\Delta DFC\) là hai tam giác vuông có góc nhọn chung \(C\) do đó chúng đồng dạng với nhau.

Từ \(\Delta ABC \backsim \Delta DFC\) ta có:

\(\dfrac{{DC}}{{AC}} = \dfrac{{DF}}{{AB}} \Rightarrow AB = \dfrac{{AC.DF}}{{DC}}\)

Thay số liệu vào biểu thức \(x = \dfrac{{\left( {m + n} \right).a}}{n}\).