Phần câu hỏi bài 4 trang 80 Vở bài tập toán 8 tập 2

Câu 9

\(\Delta A'B'C' \backsim \Delta ABC\) theo tỉ số \(k = \dfrac{1}{3}\). \(\Delta ABC \backsim \Delta ABC\) theo tỉ số \(k'\) bằng:

(A) \(\dfrac{1}{3}\)            (B) \(\dfrac{1}{2}\)                      (C) \(3\)

Khoanh tròn vào chữ cái đứng trước khẳng định đúng.

Phương pháp giải:

Tam giác \(\Delta A'B'C' \backsim \Delta ABC\) theo tỉ số \(k\) thì \(\Delta ABC \backsim \Delta A'B'C'\) theo tỉ số \(\dfrac{1}{k}\). 

Lời giải chi tiết:

Tam giác \(\Delta A'B'C' \backsim \Delta ABC\) theo tỉ số \(k = \dfrac{1}{3}\) thì \(\Delta ABC \backsim \Delta A'B'C'\) theo tỉ số \(\dfrac{1}{k} = 3\).

Chọn C. 

Câu 10

\(\Delta ABC \backsim \Delta DEF\) theo tỉ số \({k_1} = \dfrac{1}{2}\), \(\Delta DEF \backsim \Delta PMN\) theo tỉ số \({k_2} = \dfrac{1}{3}\). Khi đó \(\Delta ABC \backsim \Delta PMN\) theo tỉ số \({k_3}\) bằng:

A. \(\dfrac{5}{6}\)                         B. \(\dfrac{1}{6}\)

C. \(\dfrac{2}{3}\)                         D. \(\dfrac{3}{2}\)

Khoanh tròn vào chữ cái đứng trước khẳng định đúng.

Phương pháp giải:

\(\Delta ABC \backsim \Delta DEF\) theo tỉ số \({k_1}\), \(\Delta DEF \backsim \Delta PMN\) theo tỉ số \({k_2}\). Khi đó \(\Delta ABC \backsim \Delta PMN\) theo tỉ số \({k_3} = {k_1}{k_2}\). 

Lời giải chi tiết:

\(\Delta ABC \backsim \Delta DEF\) theo tỉ số \({k_1} = \dfrac{1}{2}\), \(\Delta DEF \backsim \Delta PMN\) theo tỉ số \({k_2} = \dfrac{1}{3}\).

Khi đó \(\Delta ABC \backsim \Delta PMN\) theo tỉ số \({k_3} = {k_1}{k_2} = \dfrac{1}{2}.\dfrac{1}{3} = \dfrac{1}{6}\).

Chọn B.

Câu 11

\(\Delta A'B'C' \backsim \Delta ABC\) theo tỉ số \({k_1} = \dfrac{1}{3}\), \(\Delta A''B''C'' \backsim \Delta ABC\) theo tỉ số \({k_2} = \dfrac{1}{3}\) (h.23). Khi đó \(\Delta A'B'C' \backsim \Delta A''B''C''\) theo tỉ số \({k_3}\) bằng:

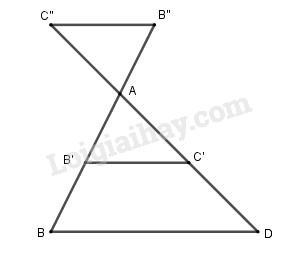
(A) \(\dfrac{1}{6}\)                   (B) \(\dfrac{1}{9}\)                     (C) \(1\)

Khoanh tròn vào chữ cái đứng trước khẳng định đúng.

Phương pháp giải:

Sử dụng tính chất của tam giác đồng dạng: 

- Tam giác \(\Delta A'B'C' \backsim \Delta ABC\) theo tỉ số \(k\) thì \(\Delta ABC \backsim \Delta A'B'C'\) theo tỉ số \(\dfrac{1}{k}\).

- \(\Delta ABC \backsim \Delta DEF\) theo tỉ số \({k_1}\), \(\Delta DEF \backsim \Delta PMN\) theo tỉ số \({k_2}\). Khi đó \(\Delta ABC \backsim \Delta PMN\) theo tỉ số \({k_3} = {k_1}{k_2}\).

Lời giải chi tiết:

\(\Delta A'B'C' \backsim \Delta ABC\) theo tỉ số \({k_1} = \dfrac{1}{3}\).

\(\Delta A''B''C'' \backsim \Delta ABC\) theo tỉ số \({k_2} = \dfrac{1}{3}\)\( \Rightarrow \Delta ABC \backsim \Delta A''B''C''\) theo tỉ số \({k_2}' = \dfrac{1}{{{k_2}}} = 3\)

Khi đó \(\Delta A'B'C' \backsim \Delta A''B''C''\) theo tỉ số \({k_3} = {k_1}.{k_2}' = \dfrac{1}{3}.3 = 1\).

Chọn C.