Giải mục I trang 67, 68 SGK Toán 10 tập 2 - Cánh diều

HĐ Khởi động

Lời giải chi tiết:

Để xác định tọa độ của máy bay trực thăng ta sử dụng biểu thức tọa độ của 2 vectơ

Hoạt động 1

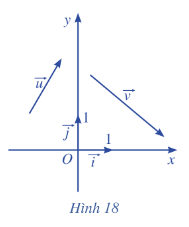
Trong mặt phẳng toạ độ Oxy (Hình 18), cho hai vectơ \(\overrightarrow u  = \left( {{x_1},{y_1}} \right)\) và \(\overrightarrow v  = \left( {{x_2},{y_2}} \right)\)

a) Biểu diễn các vectơ \(\overrightarrow u ,\overrightarrow v \) theo hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \)

b) Biểu diễn các vectơ \(\overrightarrow u  + \overrightarrow v \),\(\overrightarrow u  - \overrightarrow v \),\(k\overrightarrow u \left( {k \in \mathbb{R}} \right)\) theo hai vectơ \(\overrightarrow i \) và \(\overrightarrow j \)

c) Tìm tọa độ của các vectơ \(\overrightarrow u  + \overrightarrow v \),\(\overrightarrow u  - \overrightarrow v \),\(k\overrightarrow u \left( {k \in \mathbb{R}} \right)\)

Lời giải chi tiết:

a) Do \(\overrightarrow u  = \left( {{x_1},{y_1}} \right)\), \(\overrightarrow v  = \left( {{x_2},{y_2}} \right)\) nên \(\overrightarrow u  = {x_1}\overrightarrow i  + {y_1}\overrightarrow j .\), \(\overrightarrow v  = {x_2}\overrightarrow i  + {y_2}\overrightarrow j .\)

b) +) \(\overrightarrow u  + \overrightarrow v  = \left( {{x_1}\overrightarrow i  + {y_1}\overrightarrow j } \right) + \left( {{x_2}\overrightarrow i  + {y_2}\overrightarrow j } \right) = \left( {{x_1}\overrightarrow i  + {x_2}\overrightarrow i } \right) + \left( {{y_1}\overrightarrow j  + {y_2}\overrightarrow j } \right) = \left( {{x_1} + {x_2}} \right)\overrightarrow i  + \left( {{y_1} + {y_2}} \right)\overrightarrow j \)

+) \(\overrightarrow u  - \overrightarrow v  = \left( {{x_1}\overrightarrow i  + {y_1}\overrightarrow j } \right) - \left( {{x_2}\overrightarrow i  + {y_2}\overrightarrow j } \right) = \left( {{x_1}\overrightarrow i  - {x_2}\overrightarrow i } \right) + \left( {{y_1}\overrightarrow j  - {y_2}\overrightarrow j } \right) = \left( {{x_1} - {x_2}} \right)\overrightarrow i  + \left( {{y_1} - {y_2}} \right)\overrightarrow j \)

+) \(k\overrightarrow u  = \left( {k{x_1}} \right)\overrightarrow i  + \left( {k{y_1}} \right)\overrightarrow j \)

c) Tọa độ của các vectơ \(\overrightarrow u  + \overrightarrow v \),\(\overrightarrow u  - \overrightarrow v \),\(k\overrightarrow u \left( {k \in \mathbb{R}} \right)\)lần lượt là:

\(\left( {{x_1} + {x_2};{y_1} + {y_2}} \right),\left( {{x_1} - {x_2};{y_1} - {y_2}} \right),\left( {k{x_1},k{y_1}} \right)\)

Luyện tập – vận dụng 1

a) Cho \(\overrightarrow u  = \left( { - 2;0} \right),\overrightarrow v  = \left( {0;6} \right),\overrightarrow w  = \left( { - 2;3} \right)\). Tìm tọa độ vectơ \(\overrightarrow u  + \overrightarrow v  + \overrightarrow w \)

b) Cho \(\overrightarrow u  = \left( {\sqrt 3 ;0} \right),\overrightarrow v  = \left( {0;\sqrt 7 } \right)\). Tìm tọa độ của vectơ \(\overrightarrow w \)sao cho \(\overrightarrow w  + \overrightarrow u  = \overrightarrow v \)

Lời giải chi tiết:

a) Tọa độ của vectơ \(\overrightarrow u  + \overrightarrow v  + \overrightarrow w \) là: \(\overrightarrow u  + \overrightarrow v  + \overrightarrow w  = \left( { - 2 + 0 + \left( { - 2} \right);0 + 6 + 3} \right) = \left( { - 4;9} \right)\)

b) Ta có: \(\overrightarrow w  + \overrightarrow u  = \overrightarrow v  \Leftrightarrow \overrightarrow w  = \overrightarrow v  - \overrightarrow u \) nên \(\overrightarrow w  = \left( {0 - \sqrt 3 ; - \sqrt 7  - 0} \right) = \left( { - \sqrt 3 ; - \sqrt 7 } \right)\)

Luyện tập – vận dụng 2

Trong bài toán mở đầu, hãy tìm tọa độ của máy bay trực thăng tại thời điểm sau khi xuất phát 2 giờ.          

Phương pháp giải:

Sau khi xuất phát được 2 giờ tức là máy bay đi được \(\frac{2}{3}\) quãng đường thì ta có máy bay ở điểm M hay là ta có \(\overrightarrow {AM}  = \frac{2}{3}\overrightarrow {AB} \)

Tọa độ vectơ \(\overrightarrow {AB}  = \left( { - 300;400} \right) \Rightarrow \overrightarrow {AM}  = \left( { - 200;\frac{{800}}{3}} \right) \Rightarrow \overrightarrow {OM}  = \overrightarrow {AM}  - \overrightarrow {AO}  = \left( { - 600;\frac{{650}}{3}} \right)\)

Vậy tọa độ máy bay sau 2 giờ xuất phát là:  \(\left( { - 600;\frac{{650}}{3}} \right)\)