Giải mục 3 trang 85, 86 SGK Toán 10 tập 2 - Kết nối tri thức
Có ba hộp A, B, C. Hộp A có chứa ba thẻ mang số 1, số 2 và số 3. Hộp B chứa hai thẻ mang số 2 và số 3. Hộp C chứa hai thẻ mang số 1 và số 2. Từ mỗi hộp ta rút ra ngẫu nhiên một thẻ.
HĐ3
Cho E là một biến cố và \(\Omega \) là không gian mẫu. Tính n(\(\overline E \)) theo n(\(\Omega \)) và n(E).
Lời giải chi tiết:
Ta có \(n\left( {\overline E } \right) = n\left( \Omega \right) - n\left( E \right)\).
Luyện tập 4
Có ba hộp A, B, C. Hộp A có chứa ba thẻ mang số 1, số 2 và số 3. Hộp B chứa hai thẻ mang số 2 và số 3. Hộp C chứa hai thẻ mang số 1 và số 2. Từ mỗi hộp ta rút ra ngẫu nhiên một thẻ.
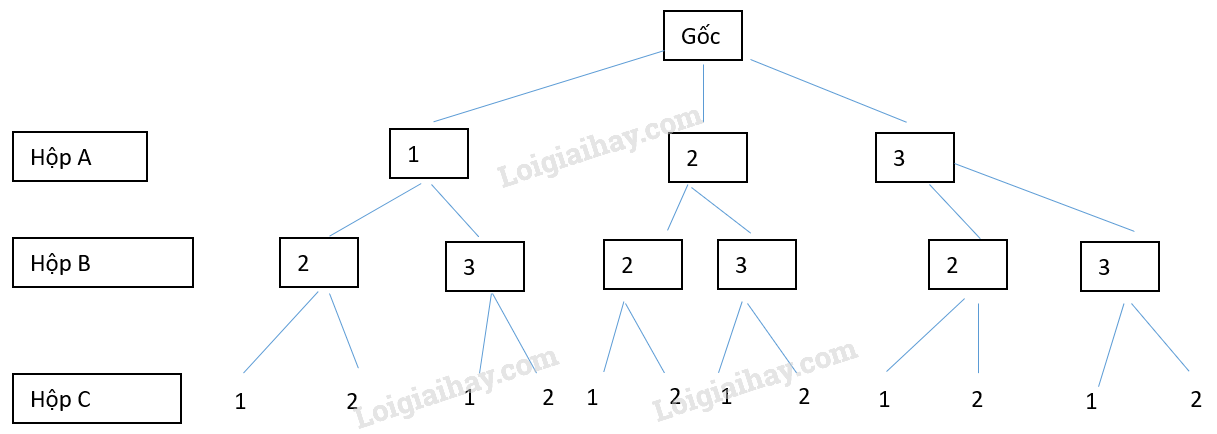
a) Vẽ sơ đồ hình cây để mô tả các phần tử của không gian mẫu.
b) Gọi M là biến cố: “Trong ba thẻ rút ra có ít nhất một thẻ số 1". Biến cố \(\overline M \) là tập con nào của không gian mẫu?
c) Tính P(M) và P(\(\overline M \)).
Lời giải chi tiết:
a) Vẽ sơ đồ cây ba tầng.
b) Chuyển qua biến cố đối: Từ sơ đồ cây xác định không gian mẫu và biến cố \(\overline M \): “Trong ba thẻ rút ra không có thẻ số 1”.
Vận dụng
Giải bài toán trong tình huống mở đầu.
Lời giải chi tiết:
Ta có \(P\left( F \right) = \frac{{n\left( F \right)}}{{n\left( \Omega \right)}} = \frac{1}{{C_{45}^6}} = \frac{1}{{8145060}}\) và \(P\left( G \right) = \frac{{n\left( G \right)}}{{n\left( \Omega \right)}} = \frac{{234}}{{C_{45}^6}} = \frac{{39}}{{1357510}}\).
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 3 trang 85, 86 SGK Toán 10 tập 2 - Kết nối tri thức timdapan.com"







