Giải mục 3 trang 8 SGK Toán 10 tập 2 - Kết nối tri thức
Quan sát bảng giá cước taxi bốn chỗ trong Hình 6.7. a) Tính số tiền phải trả khi di chuyển 25 km. b) Lập công thức tính số tiền cước taxi phải trả theo số kilômét di chuyển. c) Vẽ đồ thị và cho biết hàm số đồng biến trên khoảng nào, nghịch biến trên khoảng nào.
HĐ5
Cho hàm số \(y = - x + 1\) và \(y = x\). Tính giá trị y theo giá trị x để hoàn thành bảng sau:

Khi giá trị x tăng, giá trị y tương ứng của mỗi hàm số \(y = - x + 1\) và \(y = x\) tăng hay giảm?
Lời giải chi tiết:
Thay x vào ta có:

Dựa vào bảng trên ta thấy:
Khi x tăng, giá trị y của hàm số y=-x+1 giảm
Khi x tăng, giá trị y của hàm số y=x tăng
HĐ6
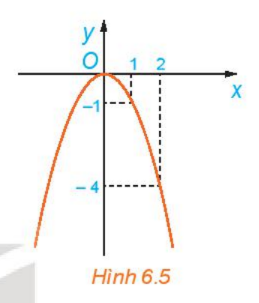
Quan sát đồ thị của hàm số \(y = f(x) = - {x^2}\) trên \(\mathbb{R}\)(H.6.5).
a) Giá trị của f(x) tăng hay giảm khi x tăng trên khoảng \(( - \infty ;0)\)?
b) Giá trị của f(x) tăng hay giảm khi x tăng trên khoảng \((0; + \infty )\)?
Lời giải chi tiết:
Dựa vào đồ thị, ta thấy:
a) Trên khoảng \(\left( { - \infty ;0} \right)\) , giá trị của f(x) tăng
b) Trên khoảng \(\left( {0; + \infty } \right)\) , giá trị của f(x) giảm
Luyện tập 3
Vẽ đồ thị của hàm số \(y = 3x + 1\) và \(y = - 2{x^2}\). Hãy cho biết:
a) Hàm số \(y = 3x + 1\)đồng biến hay nghịch biến trên \(\mathbb{R}\)
b) Hàm số \(y = - 2{x^2}\)đồng biến hay nghịch biến trên \(( - \infty ;0)\) và \((0; + \infty )\).
Phương pháp giải:
Quan sát đồ thị hàm số trên (a;b)
Hàm số đồng biến nếu đồ thị có dạng đi lên từ trái sang phải.
Hàm số nghịch biến nếu đồ thị có dạng đi xuống từ trái sang phải.
Lời giải chi tiết:
Vẽ đồ thị \(y = 3x + 1;y = - 2{x^2}\)
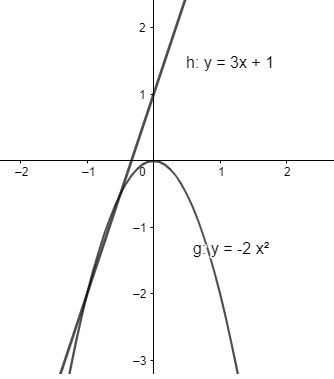
a) Trên \(\mathbb{R}\), đồ thị \(y = 3x + 1\) đi lên từ trái sang phải, như vậy hàm số \(y = 3x + 1\) đồng biến trên \(\mathbb{R}\)
b) Trên khoảng \(\left( { - \infty ;0} \right)\), đồ thị \(y = - 2{x^2}\)đi lên từ trái sang phải với mọi \(x \in \left( { - \infty ;0} \right)\) , như vậy hàm số đồng biến trên \(\left( { - \infty ;0} \right)\)
Trên khoảng \(\left( {0; + \infty } \right)\), đồ thị \(y = - 2{x^2}\)đi xuống từ trái sang phải với mọi \(x \in \left( {0; + \infty } \right)\) , như vậy hàm số nghịch biến trên \(\left( {0; + \infty } \right)\)
Vận dụng 2
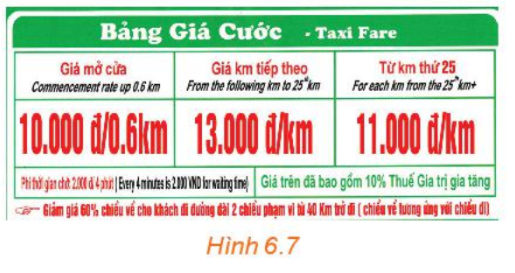
Quan sát bảng giá cước taxi bốn chỗ trong Hình 6.7.
a) Tính số tiền phải trả khi di chuyển 25 km.
b) Lập công thức tính số tiền cước taxi phải trả theo số kilômét di chuyển.
c) Vẽ đồ thị và cho biết hàm số đồng biến trên khoảng nào, nghịch biến trên khoảng nào.
Lời giải chi tiết:
Gọi x là số km taxi đã đi; y (nghìn đồng) là số tiền cước phải trả
a) Khi di chuyển 25km thì
Với 0,6km đầu tiên, số tiền cước phải trả 10000 (đồng)
Với những km tiếp theo, số tiền cước phải trả 13000.(25-0,6)=317200(đồng)
Vậy số tiền cước phải trả 317200+10000=327200(đồng)
b) Khi hành khách đi từ 0km đến 0,6km thì \(y = 10\)(nghìn đồng)
Khi hành khách đi từ 0,7km đến 25km thì \(y = 10 + (x - 0,6).13 = 13x + 2,2\)(nghìn đồng)
Khi khách hàng đi từ 25km trở lên \(y = 13.25 + 2,2 + (x - 25).11 = 11x + 52,2\) (nghìn đồng)
c) Vẽ đồ thị hàm số
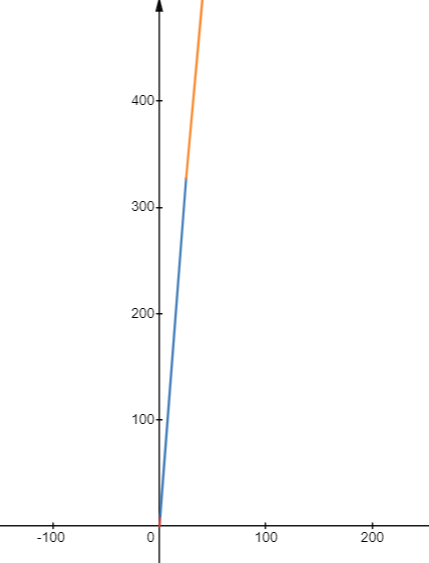
Nhìn trên đồ thị ta có thể thấy đồ thị đồng biến trên \(\left( {0; + \infty } \right)\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 3 trang 8 SGK Toán 10 tập 2 - Kết nối tri thức timdapan.com"







