Giải mục 2 trang 76, 77, 78 SGK Toán 8 - Cùng khám phá
Từ định nghĩa và tính chất của hình bình hành
Hoạt động 1
Từ định nghĩa và tính chất của hình bình hành, ta có thể suy ra tính chất nào về cạnh, góc và đường chéo của hình thoi \(ABCD\)?
Phương pháp giải:
Áp dụng định nghĩa và tính chất của hình bình hành để suy ra tính chất về cạnh, góc và đường chéo của hình thoi \(ABCD\).
Lời giải chi tiết:
Trong hình thoi:
Có các cạnh bằng nhau
Có các cặp góc đối bằng nhau.
Hai đường chéo cắt nhau tại trung điểm của mỗi đường
Hoạt động 2
Cho hình thoi \(ABCD\) (Hình 3.66).
a) Tam giác \(ABC\) là tam giác gì?
b) Vì sao \(BO\) là đường trung tuyến của tam giác \(ABC\)?
c) Em rút ra thêm được tính chất gì về hai đường chéo của hình thoi?

Phương pháp giải:
Dựa vào định nghĩa và các tính chất của hình bình hành và hình thoi để xác định.
Lời giải chi tiết:
a) Xét \(\Delta ABC\) ta có:
\(AB = BC\) (vì \(ABCD\) là hình thoi)
→ \(\Delta ABC\) là tam giác cân
b) Ta có:
\(AC\) và \(BD\) là hai đường chéo của hình thoi \(ABCD\)
Nên O là trung điểm của \(AC\) và \(BD\).
→ \(BO\) là đường trung tuyến của tam giác \(ABC\)
c) Vì \(BO\) là đường trung tuyến của tam giác \(ABC\)
Mà \(\Delta ABC\) là tam giác cân
→ \(BO \bot AC\)
→ Hai đường chéo của hình thoi vuông góc với nhau.
Luyện tập 1
Hình thoi \(MNPQ\) có \(\widehat {NMQ} = 124^\circ \). Tính số đo góc \(MNQ\).
Phương pháp giải:
Áp dụng tính chất của hình thoi để tính số đo góc \(MNQ\).
Lời giải chi tiết:
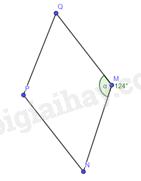
Gọi số đo góc \(MNQ\) là \(x\) =>\(\widehat {MNQ} = \widehat {MQN} = x\)
Xét tam giác cân \(QMN\), ta có:
\(\begin{array}{l}124^\circ + x + x = 180^\circ \\ = > x = \frac{{180^\circ - 124^\circ }}{2} = 28^\circ \end{array}\)
Vậy số đo góc \(MNQ\) là \(28^\circ \).
Vận dụng 1
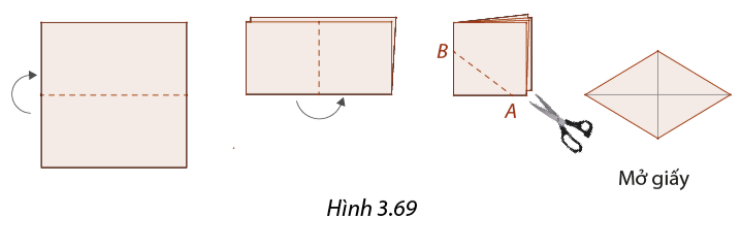
Gấp một tờ giấy làm tư như Hình 3.69 và cắt chéo theo đường \(AB\) bất kì (\(A,B\) nằm trên hai mép gấp). Sau khi mở giấy, tứ giác cắt được là hình gì? Vì sao?
Phương pháp giải:
Dựa vào định nghĩa và tính chất của hình thoi để xác định.
Lời giải chi tiết:
Sau khi mở giấy, tứ giác cắt được là hình thoi.
Bởi vì khi gấp giấy làm bốn và cắt chéo một đường \(AB\) thì sẽ được 4 đường thẳng bằng \(AB\) và 4 đường thẳng đó chính là 4 cạnh của tứ giác sau khi mở giấy. Mà tứ giác có bốn cạnh bằng nhau là hình thoi.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 2 trang 76, 77, 78 SGK Toán 8 - Cùng khám phá timdapan.com"







