Giải mục 2 trang 61, 62 SGK Toán 10 tập 2 - Chân trời sáng tạo
Viết phương trình tiếp tuyến của đường tròn (C) tại điểm A(4;6) Một vận động viên ném đĩa đã vung đĩa theo một đường tròn (C) có phương trình:
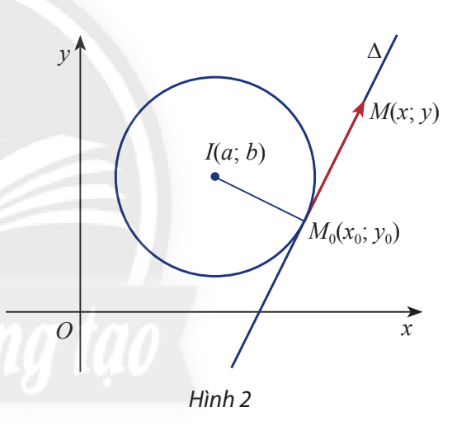
HĐ Khám phá 2
Cho điểm \({M_0}\left( {{x_0};{y_0}} \right)\) nằm trên đường tròn \((C)\) tâm \(I(a;b)\)và cho điểm\(M(x;y)\) tùy ý trong mặt phẳng Oxy. Gọi \(\Delta \) là tiếp tuyến với \((C)\) tại \({M_0}\)
a) Viết biểu thức tọa độ của hai vt \(\overrightarrow {{M_0}M} \) và \(\overrightarrow {{M_0}I} \)
b) Viết biểu thức tọa độ của tích vô hướng của hai vt \(\overrightarrow {{M_0}M} \) và \(\overrightarrow {{M_0}I} \)
c) Phương trình \(\overrightarrow {{M_0}M} .\overrightarrow {{M_0}I} = 0\)là phương trình của đường thẳng nào?
Phương pháp giải:
a) Với \(A(a;b),B(x;y)\) thì tọa độ của vt \(\overrightarrow {AB} = (x - a;y - b)\)
b) Với \(\overrightarrow a = \left( {a,b} \right),\overrightarrow b = (x;y)\) thì \(\overrightarrow a .\overrightarrow b = ax + by\)
c) Từ tích vô hướng đưa ra kết luận là \(\overrightarrow {{M_0}M} = \left( {x - {x_0};y - {y_0}} \right)\), \(\overrightarrow {{M_0}I} = \left( {a - {x_0};b - {y_0}} \right)\)
Lời giải chi tiết:
a) Biểu thức tọa độ của hai vt \(\overrightarrow {{M_0}M} \) và \(\overrightarrow {{M_0}I} \) là \(\overrightarrow {{M_0}M} = \left( {x - {x_0};y - {y_0}} \right)\), \(\overrightarrow {{M_0}I} = \left( {a - {x_0};b - {y_0}} \right)\)
b) Ta có:
\(\overrightarrow {{M_0}M} .\overrightarrow {{M_0}I} = \left( {x - {x_0}} \right)\left( {a - {x_0}} \right) + \left( {b - {y_0}} \right)\left( {y - {y_0}} \right)\)
c) \(\overrightarrow {{M_0}M} .\overrightarrow {{M_0}I} = 0 \Rightarrow \overrightarrow {{M_0}M} \bot \overrightarrow {{M_0}I} \)
Mà \({M_0}I\) là đoạn thẳng nối tâm với điểm nằm ngoài
Vậy ta thấy pt đường thẳng \(M{M_0}\) là tiếp tuyến của đường tròn tại điểm \({M_0}\)
Thực hành 3
Viết phương trình tiếp tuyến của đường tròn \((C):{x^2} + {y^2} - 2x - 4y - 20 = 0\) tại điểm \(A(4;6)\)
Phương pháp giải:
Phương trình tiếp tuyến của đường tròn tâm \(I(a;b)\) tại điểm \(M({x_0};{y_0})\)nằm trên đường tròn là: \(\left( {a - {x_0}} \right)\left( {x - {x_0}} \right) + \left( {b - {y_0}} \right)\left( {y - {y_0}} \right) = 0\)
Lời giải chi tiết:
Ta có \({4^2} + {6^2} - 2.4 - 4.6 - 20 = 0\), nên điểm A thuộc (C)
Đường tròn \((C):{x^2} + {y^2} - 2x - 4y - 20 = 0\) có tâm \(I(1;2)\)
Phương trình tiếp tuyến d của (C) tại \(A(4;6)\) là:
\(\begin{array}{l}\left( {4 - 1} \right)\left( {x - 4} \right) + \left( {6 - 2} \right)\left( {y - 6} \right) = 0\\ \Leftrightarrow 3x + 4y + 16 = 0\end{array}\)
Vận dụng 3
Một vận động viên ném đĩa đã vung đĩa theo một đường tròn \((C)\) có phương trình:
\({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = \frac{{169}}{{144}}\).
Khi người đó vung đĩa đến vị trí điểm \(M\left( {\frac{{17}}{{12}};2} \right)\) thì buông đĩa (hình 4). Viết phương trình tiếp tuyến của đường tròn \((C)\) tại điểm M
Phương pháp giải:
Phương trình tiếp tuyến của đường trong tâm \(I(a;b)\) tại điểm \(M({x_0};{y_0})\)nằm trên đường tròn là: \(\left( {a - {x_0}} \right)\left( {x - {x_0}} \right) + \left( {b - {y_0}} \right)\left( {y - {y_0}} \right) = 0\)
Lời giải chi tiết:
Ta có \({\left( {\frac{{17}}{{12}} - 1} \right)^2} + {\left( {2 - 1} \right)^2} = \frac{{169}}{{144}}\), nên điểm M thuộc (C)
Đường tròn \({\left( {x - 1} \right)^2} + {\left( {y - 1} \right)^2} = \frac{{169}}{{144}}\) có tâm \(I(1;1)\)
Phương trình tiếp tuyến d của (C) tại \(M\left( {\frac{{17}}{{12}};2} \right)\) là:
\(\begin{array}{l}\left( {\frac{{17}}{{12}} - 1} \right)\left( {x - \frac{{17}}{{12}}} \right) + \left( {2 - 1} \right)\left( {y - 2} \right) = 0\\ \Leftrightarrow \frac{5}{2}x + y - \frac{{133}}{{24}} = 0\end{array}\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 2 trang 61, 62 SGK Toán 10 tập 2 - Chân trời sáng tạo timdapan.com"