Giải mục 2 trang 17, 18 Chuyên đề học tập Toán 11 - Kết nối tri thức
Khi mặt bàn ăn quay, mặc dù các đĩa thức ăn trên bàn đều dịch chuyển tới vị trí mới nhưng khoảng cách giữa hai đĩa thức ăn có bị thay đổi hay không?
Hoạt động 2
Khi mặt bàn ăn quay, mặc dù các đĩa thức ăn trên bàn đều dịch chuyển tới vị trí mới nhưng khoảng cách giữa hai đĩa thức ăn có bị thay đổi hay không?
Phương pháp giải:
Suy luận thực tiễn để trả lời
Lời giải chi tiết:
Khoảng cách giữa hai đĩa thức ăn không bị thay đổi khi mặt bàn ăn quay.
Luyện tập 2
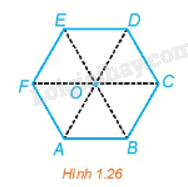
Trong Hình 1.26, ABCDEF là lục giác đều có tâm O. Tìm ảnh của tam giác ACE qua các phép quay \({Q_{\left( {O,\,\frac{\pi }{3}} \right)}},\,\,{Q_{\left( {O,\, - \frac{{2\pi }}{3}} \right)}}\)
Phương pháp giải:
Phép quay tâm O, góc quay :
Khi đó, \(\left\{ \begin{array}{l}x' = x\cos \alpha - y\sin \alpha \\y' = x\sin \alpha + y\cos \alpha \end{array} \right.\)
Lời giải chi tiết:
Ta có: ABCDEF là lục giác đều nên
\(\widehat {AOB} = \widehat {BOC} = \widehat {COD} = \widehat {DOE} = \widehat {EOF} = \widehat {FOA} = 60^\circ = \frac{\pi }{3}\) và \(OA{\rm{ }} = {\rm{ }}OB{\rm{ }} = {\rm{ }}OC{\rm{ }} = {\rm{ }}OD{\rm{ }} = {\rm{ }}OE{\rm{ }} = {\rm{ }}OF\).
Do đó, phép quay \({Q_{\left( {O,\frac{\pi }{3}} \right)}}\) biến các điểm A, C, E tương ứng thành các điểm B, D, F.
Vậy phép quay \({Q_{\left( {O,\frac{\pi }{3}} \right)}}\) biến tam giác ACE thành tam giác BDF.
Ta có: \(\widehat {AOE} = \widehat {AOF} + \widehat {EOF} = \frac{{2\pi }}{3}\), tương tự \(\widehat {COA} = \widehat {EOC} = \frac{{2\pi }}{3}\)
Vì OA = OE và góc quay \( - \frac{{2\pi }}{3}\) nên phép quay \({Q_{\left( {O,\, - \frac{{2\pi }}{3}} \right)}}\) biến điểm A thành điểm E.
Vì OC = OA và góc quay \( - \frac{{2\pi }}{3}\) nên phép quay \({Q_{\left( {O,\, - \frac{{2\pi }}{3}} \right)}}\) biến điểm C thành điểm A.
Vì OE = OC và góc quay \( - \frac{{2\pi }}{3}\) nên phép quay \({Q_{\left( {O,\, - \frac{{2\pi }}{3}} \right)}}\) biến điểm E thành điểm C.
Vậy phép quay \({Q_{\left( {O,\, - \frac{{2\pi }}{3}} \right)}}\) biến tam giác ACE thành tam giác ECA hay biến tam giác ACE thành chính nó.
Vận dụng 1
Trong tình huống mở đầu, mặt bàn tròn đặt đồ ăn được thiết kế để có thể quay quanh tâm mặt bàn. Coi mặt bàn tròn là hình tròn tâm O, bán kính R. Hỏi, khi thực hiện phép quay tâm O với góc quay \(\alpha \) bất kì thì:
- Điểm O biến thành điểm nào?
- Đường tròn (O, R) biến thành đường tròn nào?
- Vị trí của mặt bàn có bị dịch chuyển hay không?
Phương pháp giải:
Trong mặt phẳng, cho điểm O cố định và góc lượng giác \(\alpha \) không đổi. Phép biến hình biến điểm O thành điểm O và biến mỗi điểm M khác O thành M’ sao cho \(OM = OM'\) và góc lượng giác \(\left( {OM,OM'} \right) = \alpha \) được gọi là phép quay tâm O với góc quay \(\alpha \), kí hiệu \({Q_{\left( {O,\alpha } \right)}}\). O gọi là tâm quay, \(\alpha \) gọi là góc quay.
Lời giải chi tiết:
Điểm O là tâm quay nên khi thực hiện phép quay tâm O với góc quay α bất kì thì điểm O biến thành điểm O, đường tròn (O; R) biến thành đường tròn (O; R).
Vậy vị trí của mặt bàn không bị dịch chuyển.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 2 trang 17, 18 Chuyên đề học tập Toán 11 - Kết nối tri thức timdapan.com"







