Giải bài 1.12 trang 20 Chuyên đề học tập Toán 11 Kết nối tri thức

Đề bài

Cho hình vuông ABCD có tâm O. Trên đường tròn ngoại tiếp hình vuông, theo chiều dương (ngược chiều kim đồng hồ), thứ tự các đỉnh hình vuông là A, B, C, D.

a) Tìm ảnh của các điểm A, B, C, D qua phép quay tâm O góc quay \(\;\frac{\pi }{2}\).

b) Mỗi phép quay \({Q_{(O,{\rm{ }}o)}},\)\({Q_{\left( {O,\,\frac{\pi }{2}} \right)}},\,{Q_{\left( {O,\,\pi } \right)}},\,{Q_{\left( {O,\,\frac{{3\pi }}{2}} \right)}}\) biến hình vuông ABCD thành hình nào?

Lời giải chi tiết

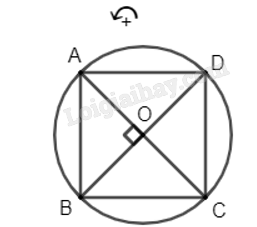
a) Vì ABCD là hình vuông nên hai đường chéo AC và BD vuông góc với nhau tại tâm O và OA = OB = OC = OD.

Khi đó, phép quay \({Q_{\left( {O,\,\frac{\pi }{2}} \right)}}\) biến các điểm A, B, C, D tương ứng thành các điểm B, C, D, A.

b) Phép quay \({Q_{(O,{\rm{ }}o)}}\) biến hình vuông ABCD thành hình vuông ABCD.

Từ câu a, suy ra phép quay \({Q_{\left( {O,\,\frac{\pi }{2}} \right)}}\) biến hình vuông ABCD thành hình vuông BCDA.

Phép quay \({Q_{\left( {O,\,\pi } \right)}}\) biến các điểm A, B, C, D tương ứng thành các điểm C, D, A, B. Do đó phép quay Q_{(O, π)} biến hình vuông ABCD thành hình vuông CDAB.

Phép quay \({Q_{\left( {O,\,\frac{{3\pi }}{2}} \right)}}\) biến các điểm A, B, C, D tương ứng thành các điểm D, A, B, C. Do đó phép quay \({Q_{\left( {O,\,\frac{{3\pi }}{2}} \right)}}\) biến hình vuông ABCD thành hình vuông DABC.