Giải mục 2 trang 113, 114 SGK Toán 8 tập 1 - Cánh diều
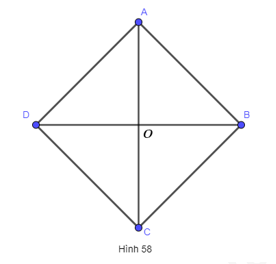
Cho hình thoi ABCD có hai đường chéo là AC và BD cắt nhau tại O (hình 58) a) Hình thoi ABCD có là hình bình hành hay không? b) Hai đường chéo AC và BD có vuông góc với nhau hay không? c) Hai tam giác ABC và ADC có bằng nhau hay không? Tia AC có phải là tia phân giác của \(\widehat {BA{\rm{D}}}\) hay không?
HĐ2
Cho hình thoi ABCD có hai đường chéo là AC và BD cắt nhau tại O (hình 58)
a) Hình thoi ABCD có là hình bình hành hay không?
b) Hai đường chéo AC và BD có vuông góc với nhau hay không?
c) Hai tam giác ABC và ADC có bằng nhau hay không? Tia AC có phải là tia phân giác của \(\widehat {BA{\rm{D}}}\) hay không?
Phương pháp giải:
Quan sát hình và chứng minh các tam giác tương ứng bằng nhau
Lời giải chi tiết:
a) Hình thoi ABCD có là hình bình hành (vì AB = BC = CD = DA)
b) Xét tam giác ABC có AB = AC nên tam giác ABC là tam giác cân tại A.
Suy ra đường trung tuyến AO đồng thời là đường cao.
Suy ra AO vuông góc với BC
Hay AD vuông góc với BC
c) Xét tam giác ABC và tam giác ADC có:
AD = AB
CD = CB
AC chung
\(\begin{array}{l}\Delta ABC = \Delta A{\rm{D}}C\\ \Rightarrow \widehat {DAC} = \widehat {BAC}\end{array}\)
Mà AC nằm giữa 2 tia AB và AD
Suy ra: AC là tia phân giác của góc BAD
Luyện tập vận dụng 1
Cho hình thoi ABCD có \(\widehat {ABC} = {120^o}\). Chứng minh tam giác ABD là tam giác đều.
Phương pháp giải:
Vận dụng các tính chất của hình thoi: chứng minh tam giác ABD cân tại A và có \(\widehat A = {60^o}\)
Lời giải chi tiết:
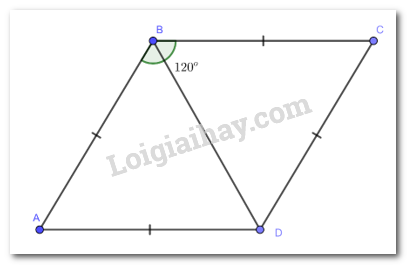
Vì ABCD là hình thoi
Suy ra: \(\widehat B = \widehat C = {120^o}\)
Mà: \(\widehat A = \widehat D\)
Mặt khác: \(\widehat A + \widehat B + \widehat C + \widehat D = {360^o}\)
Suy ra: \(\widehat A = \widehat D = \dfrac{{{{360}^o} - \widehat B - \widehat C}}{2} = \dfrac{{{{360}^o} - {{120}^o} - {{120}^o}}}{2} = {60^o}\)
Xét tam giác ABD có AB = AD nên tam giác ABD là tam giác cân tại A mà \(\widehat A = {60^o}\)
Suy ra tam giác ABD là tam giác đều
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 2 trang 113, 114 SGK Toán 8 tập 1 - Cánh diều timdapan.com"