Giải mục 1 trang 60 Chuyên đề học tập Toán 10 - Cánh diều
Quan sát Hình 22a, Hình 22b, Hình 22c và nêu tỉ số khoảng cách từ một điểm M nằm trên mỗi đường conic đến tiêu điểm của nó và khoảng cách từ điểm M đến đường chuẩn tương ứng với tiêu điểm đó.
Đề bài
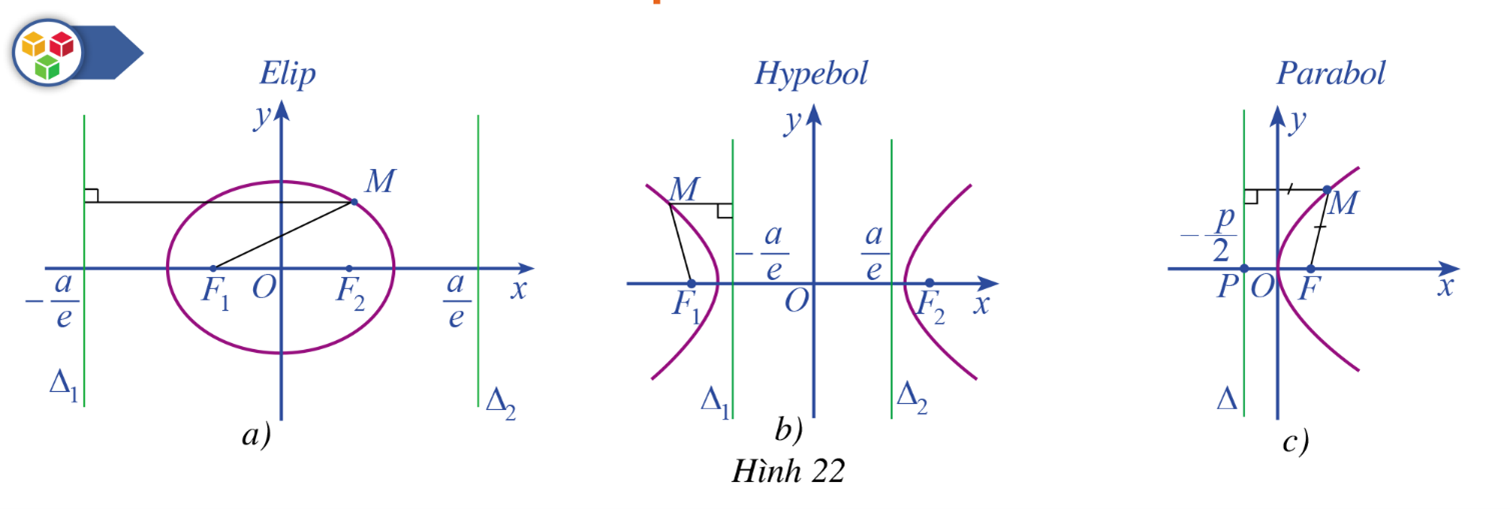
Quan sát Hình 22a, Hình 22b, Hình 22c và nêu tỉ số khoảng cách từ một điểm M nằm trên mỗi đường conic đến tiêu điểm của nó và khoảng cách từ điểm M đến đường chuẩn tương ứng với tiêu điểm đó.
Lời giải chi tiết
+ Với mọi điểm M thuộc elip (E): \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\left( {a > b > 0} \right)\), ta luôn có \(\frac{{MF}}{{d\left( {M,\Delta } \right)}} = e\left( {0 < e < 1} \right)\), trong đó F là một trong hai tiêu điểm \({F_1},{F_2}\) và \(\Delta \) là đường chuẩn ứng tiêu điểm F
+ Với mọi điểm M thuộc hypebol (H): \(\frac{{{x^2}}}{{{a^2}}} - \frac{{{y^2}}}{{{b^2}}} = 1\left( {a > 0,b > 0} \right)\), ta luôn có \(\frac{{MF}}{{d\left( {M,\Delta } \right)}} = e\left( {e > 1} \right)\), trong đó F là một trong hai tiêu điểm \({F_1},{F_2}\) và \(\Delta \) là đường chuẩn ứng tiêu điểm F
+ Với mọi điểm M thuộc parabol (P): \({y^2} = 2px\left( {p > 0} \right)\), ta luôn có \(\frac{{MF}}{{d\left( {M,\Delta } \right)}} = 1\), trong đó F là một trong hai tiêu điểm \({F_1},{F_2}\) và \(\Delta \) là đường chuẩn ứng tiêu điểm F
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 1 trang 60 Chuyên đề học tập Toán 10 - Cánh diều timdapan.com"







