Giải mục 1 trang 6, 7, 8 SGK Toán 8 - Cùng khám phá
Nhiệt độ
Hoạt động 1
Nhiệt độ \(T\left( {^\circ C} \right)\) tại các thời điểm t (giờ) trong ngày 16/10/2022 tại Thành phố Hồ Chí Minh được cho trong Bảng 5.2.

a) Hãy cho biết nhiệt độ tại Thành phố Hồ Chí Minh lúc 7 giờ, 10 giờ, 16 giờ ngày 16/10/2022.
b) Với mỗi giá trị của t có bao nhiêu giá trị tương ứng của T.
Phương pháp giải:
Quan sát Bảng 5.2 và xác định nhiệt độ tại Thành phố Hồ Chí Minh lúc 7 giờ, 10 giờ, 16 giờ ngày 16/10/2022.
Lời giải chi tiết:
a) Quan sát Bảng 5.2 ta thấy nhiệt độ tại Thành phố Hồ Chí Minh lúc 7 giờ là 230C, lúc 10 giờ là 280C, lúc 16 giờ là 320C.
b) Với mỗi giá trị của t chỉ có 1 giá trị tương ứng của T.
Hoạt động 2
Viết công thức tính diện tích \(y\left( {c{m^2}} \right)\) của hình vuông có độ dài cạnh đáy bằng x (cm). Ứng với mỗi giá trị của x, tìm được bao nhiêu giá trị tương ứng của y?
Phương pháp giải:
Áp dụng công thức tính diện tích hình vuông để xác định mỗi giá trị của x thì tìm được bao nhiêu giá trị của y.
Lời giải chi tiết:
Diện tích của hình vuông đó là:
\(y = x.x\left( {c{m^2}} \right)\)
Vậy ta thấy với mỗi giá trị của x thì chỉ tìm được 1 giá trị của y.
Hoạt động 3
Trong hộp đồ chơi lắp ráp có năm mảnh hình chữ nhật khác nhau. Diện tích \(S\left( {c{m^2}} \right)\) và chiều rộng r (cm) của các mảnh hình chữ nhật được thống kê trong Bảng 5.3.
a) Tìm chiều rộng của hình chữ nhật có diện tích \(S = 3\left( {c{m^2}} \right)\)
b) Tìm chiều rộng của hình chữ nhật có diện tích \(S = 6\left( {c{m^2}} \right)\)
c) Quan hệ giữa S và r có thỏa mãn điều kiện “cứ mỗi giá trị của S có đúng một giá trị của r” không?

Phương pháp giải:
Dựa vào dữ liệu trong Bảng 5.3 và công thức tính diện tích hình chữ nhật để tìm chiều rộng của hình chữ nhật có diện tích \(S = 3\left( {c{m^2}} \right)\) và chiều rộng của hình chữ nhật có diện tích \(S = 6\left( {c{m^2}} \right)\), sau đó đưa ra nhận xét về các giá trị.
Lời giải chi tiết:
a) Quan sát Bảng 5.3 ta thấy chiều rộng của hình chữ nhật có diện tích \(S = 3\left( {c{m^2}} \right)\) là \(r = 1\left( {cm} \right)\)
b) Quan sát Bảng 5.3 ta thấy chiều rộng của hình chữ nhật có diện tích \(S = 6\left( {c{m^2}} \right)\) là \(r = 2\left( {cm} \right)\)
c) Qua đó ta thấy cứ mỗi một giá trị của S thì cho ra đúng một giá trị của r.
Luyện tập 1
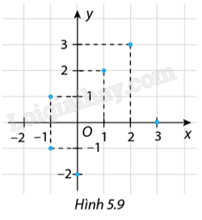
Quan hệ giữa hai đại lượng \(x,y\) được biểu diễn bởi sáu điểm cho trên mặt phẳng tọa độ ở Hình 5.9.
a) Tìm số thích hợp cho ô trống trong Bảng 5.6, với \(\left( {x;y} \right)\) là tọa độ của các điểm đã cho

b) Đại lượng y có là hàm số của đại lượng x không?
Phương pháp giải:
Dựa vào cách xác định tọa độ trong mặt phẳng tọa độ để điền vào Bảng 5.6.
Nếu đại lượng y phụ thuộc vào đại lượng thay đổi x sao cho với mỗi giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y.
Lời giải chi tiết:
a) Dựa vào các tọa độ trong Hình 5.9, ta có Bảng 5.6 như sau:

b) Quan sát Bảng 5.6 ta thấy mỗi giá trị của x luôn luôn xác định được chỉ một giá trị tương ứng của y nên y được gọi là hàm số của x và x được gọi là biến số.
Vận dụng 1
Số tiền y (nghìn đồng) khách hàng phải thanh toán khi di chuyển quãng đường x (km) bằng taxi của hãng A cho bởi công thức \(y = f\left( x \right) = 13x + 10\).
a) Đại lượng y có là hàm số của đại lượng x không?
b) Tính \(f\left( 5 \right)\). Giá trị này cho biết điều gì?
Phương pháp giải:
Xác định xem mỗi giá trị của x ta có luôn xác định được chỉ một giá trị tương ứng của y không bằng cách thay giá trị x bất kì vào y nếu giá trị của x ta luôn xác định được chỉ một giá trị tương ứng của y thì đại lượng y chính là hàm số của đại lượng x.
Thay \(x = 5\) vào công thức \(y = f\left( x \right) = 13x + 10\). Sau đó cho biết giá trị y.
Lời giải chi tiết:
a) Ta có công thức: \(y = f\left( x \right) = 13x + 10\).
Với \(x = 1\) thì \(y = 23\)
Với \(x = 2\) thì \(y = 26\)
Với \(x = 3\) thì \(y = 49\)
Vậy ta thấy với mỗi giá trị của x thì ta luôn xác định được chỉ một giá trị tương ứng y nên y được gọi là hàm số của x và x là biến của y.
b) Thay \(x = 5\) vào công thức \(y = f\left( x \right) = 13x + 10\). Ta có:
\(\begin{array}{l}y = 13.5 + 10\\ = > y = 75\end{array}\)
Với giá trị này cho ta biết số tiền mà khách hàng phải thanh toán khi di chuyển quãng đường 5 km bằng xe taxi của hãng A là 75 nghìn đồng.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 1 trang 6, 7, 8 SGK Toán 8 - Cùng khám phá timdapan.com"







