Giải mục 1 trang 30, 31, 32 SGK Toán 9 tập 2 - Cùng khám phá
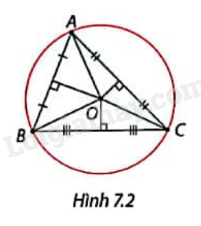
Vẽ tam giác ABC. Vẽ ba đường trung trực của tam giác ABC và xác định giao điểm O của chúng. Giải thích vì sao đường tròn tâm O bán kính OA đi qua cả ba đỉnh của (Delta )ABC. (Hình 7.2)
HĐ1
Trả lời câu hỏi Hoạt động 1 trang 30 SGK Toán 9 Cùng khám phá
Vẽ tam giác ABC. Vẽ ba đường trung trực của tam giác ABC và xác định giao điểm O của chúng. Giải thích vì sao đường tròn tâm O bán kính OA đi qua cả ba đỉnh của \(\Delta \)ABC. (Hình 7.2)
Phương pháp giải:
Ba đường trung trực của một tam giác cùng đi qua một điểm và điểm này cách đều ba đỉnh của tam giác.
Lời giải chi tiết:
Ta có ba đường trung trực của tam giác ABC cùng đi qua một điểm O nên ta có OC = OB = OA. Vì vậy đường tròn tâm O bán kính OA đi qua cả ba đỉnh của \(\Delta \)ABC.
LT1
Trả lời câu hỏi Luyện tập 1 trang 32 SGK Toán 9 Cùng khám phá
Tam giác đều ABC có cạnh bằng 4, M là trung điểm của BC và O là trọng tâm. Xác định tâm, bán kính và vẽ đường tròn ngoại tiếp tam giác ABC và AMC.
Phương pháp giải:
Đường tròn ngoại tiếp tam giác đều cạnh a có tâm là trọng tâm của tam đều có bán kính bằng \(\frac{{a\sqrt 3 }}{3}\).
Lời giải chi tiết:
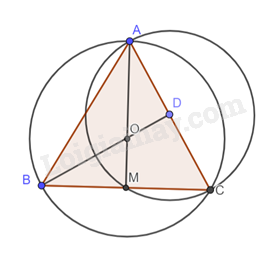
Đường tròn ngoại tiếp tam giác ABC có tâm là O, bán kính OA = \(\frac{{4\sqrt 3 }}{3}\) cm.
Đường tròn ngoại tiếp tam giác AMC có tâm là trung điểm AC là D, bán kính DA.
Ta có DA = \(\frac{1}{2}AC = \frac{1}{2}.4 = 2\) cm.
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 1 trang 30, 31, 32 SGK Toán 9 tập 2 - Cùng khám phá timdapan.com"