Giải mục 1 trang 11, 12 SGK Toán 10 tập 2 - Chân trời sáng tạo
Lợi nhuận (I) thu được trong một ngày làm việc kinh doanh một loại gạo của cửa hàng Các bất phương trình nào sau đây là bất phương trình bậc hai một ẩn? Giải các bất phương trình bậc hai sau: Hãy giải bất phương trình lập được trong hoạt động khám phá và tìm giá bán gạo sao cho cửa hàng có lãi.
HĐ Khởi động
Với giá trị nào của x thì tam thức bậc hai \(f\left( x \right) = 2{x^2} - 5x + 3\) mang dấu dương?
Phương pháp giải:
Bước 1: Xét dấu của biệt thức \(\Delta = {b^2} - 4ac\)
Bước 2: Tìm nghiệm của tam thức (nếu có), xét dấu của hệ số \(a\)
Bước 3: Lập bảng xét dấu và kết luận.
Lời giải chi tiết:
Tam thức \(f\left( x \right) = 2{x^2} - 5x + 3\) có \(\Delta = 1 > 0\), hai nghiệm phân biệt là \({x_1} = 1,{x_2} = \frac{3}{2}\) và \(a = 2 > 0\)
Ta có bảng xét dấu như sau:
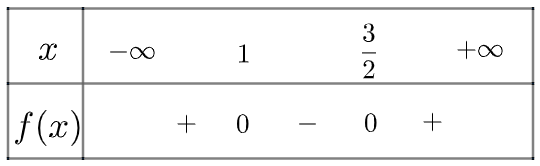
Vậy tam thức đã cho mang dấu dương khi x nằm trong khoảng \(\left( { - \infty ;1} \right) \cup \left( {\frac{3}{2}; + \infty } \right)\)
HĐ Khám phá
Lợi nhuận (I) thu được trong một ngày làm việc kinh doanh một loại gạo của cửa hàng phụ thuộc vào giá bán (x) của một kg loại gạo đó theo công thức \(I = - 3{x^2} + 200x - 2325\) với I và x được tính bằng nghìn đồng. Giá trị x như thế nào thì cửa hàng có lãi từ loại gạo đó?

Phương pháp giải:
Bước 1: Xác định của hàng có lãi thì lợi nhuận lớn hơn 0, suy ra \(I > 0\)
Bước 2: Xác định dấu của \(\Delta ,a\) và tìm nghiệm (nếu có)
Bước 3: Lập bảng xét dấu
Lời giải chi tiết:
Để cửa hàng có lãi thì lợi nhuận lớn hơn 0, suy ra \(I > 0 \Leftrightarrow - 3{x^2} + 200x - 2325 > 0\)
Tam thức \(I = - 3{x^2} + 200x - 2325\) có \(\Delta = 12100 > 0\), có hai nghiệm phân biệt \({x_1} = 15;{x_2} = \frac{{155}}{3}\) và có \(a = - 3 < 0\)
Ta có bảng xét dấu như sau:
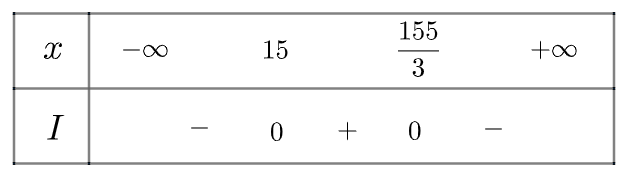
Vậy ta thấy cửa hàng có lợi nhuận khi \(x \in \left( {15;\frac{{155}}{3}} \right)\) (kg)
Thực hành 1
Các bất phương trình nào sau đây là bất phương trình bậc hai một ẩn? Nếu là bất phương trình bậc hai một ẩn, \(x = 2\) có là nghiệm của bất phương trình đó hay không?
a) \({x^2} + x - 6 \le 0\)
b) \(x + 2 > 0\)
c) \( - 6{x^2} - 7x + 5 > 0\)
Phương pháp giải:
Bước 1: Xác định bậc của bất phương trình và số ẩn, nếu bậc là 2 và có một ẩn thì là bất phương trình bậc hai một ẩn
Bước 2: Thay \(x = 2\) vào bất phương trình, nếu thỏa mãn bất phương trình thì là nghiệm
Lời giải chi tiết:
a) \({x^2} + x - 6 \le 0\) là một bất phương trình bậc hai một ẩn
Vì \({2^2} + 2 - 6 = 0\) nên \(x = 2\) là nghiệm của bất phương trình trên
b) \(x + 2 > 0\) không là bất phương trình bậc hai một ẩn
c) \( - 6{x^2} - 7x + 5 > 0\) là một bất phương trình bậc hai một ẩn
Vì \( - {6.2^2} - 7.2 + 5 = - 33 < 0\) nên \(x = 2\) không là nghiệm của bất phương trình trên
Thực hành 2
Giải các bất phương trình bậc hai sau:
a) \(15{x^2} + 7x - 2 \le 0\)
b) \( - 2{x^2} + x - 3 < 0\)
Phương pháp giải:
Bước 1: Tìm nghiệm của tam thức (nếu có)
Bước 2: Xác định dấu của a
Bước 3: Xét dấu của tam thức
Lời giải chi tiết:
a) Tam thức bậc hai \(f\left( x \right) = 15{x^2} + 7x - 2\) có hai nghiệm phân biệt là \({x_1} = - \frac{2}{3};{x_2} = \frac{1}{5}\)
và có \(a = 15 > 0\) nên \(f\left( x \right) \le 0\) khi x thuộc đoạn \(\left[ { - \frac{2}{3};\frac{1}{5}} \right]\)
Vậy tập nghiệm của bất phương trình \(15{x^2} + 7x - 2 \le 0\) là \(\left[ { - \frac{2}{3};\frac{1}{5}} \right]\)
b) Tam thức bậc hai \(f\left( x \right) = - 2{x^2} + x - 3\) có \(\Delta = - 23 < 0\) và \(a = - 2 < 0\)
nên \(f\left( x \right)\) âm với mọi \(x \in \mathbb{R}\)
Vậy bất phương trình \( - 2{x^2} + x - 3 < 0\) có tập nghiệm là \(\mathbb{R}\)
Vận dụng
Hãy giải bất phương trình lập được trong hoạt động khám phá và tìm giá bán gạo sao cho cửa hàng có lãi.
Phương pháp giải:
Bước 1: Lập bất phương trình
Bước 2: Tìm nghiệm của tam thức bậc hai (nếu có)
Bước 3: Xác định dấu của tam thức bậc hai một ẩn
Lời giải chi tiết:
Để cửa hàng có lãi thì lợi nhuận lớn hơn 0
Nên ta có bất phương trình như sau: \( - 3{x^2} + 200x - 2325 > 0\)
Tam thức bậc hai \(f\left( x \right) = - 3{x^2} + 200x - 2325\) có hai nghiệm phân biệt là \({x_1} = 15;{x_2} = \frac{{155}}{3}\) và có \(a = - 3 < 0\)
Nên \(f\left( x \right)\) dương khi x nằm trong khoảng \(\left( {15;\frac{{155}}{3}} \right)\)
Vậy bất phương trình \( - 3{x^2} + 200x - 2325 > 0\) có tập nghiệm là \(\left( {15;\frac{{155}}{3}} \right)\)
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải mục 1 trang 11, 12 SGK Toán 10 tập 2 - Chân trời sáng tạo timdapan.com"







