B. Hoạt động ứng dụng - Bài 8 : Em ôn lại những gì đã học

Đề bài

Quan sát sự tăng trưởng của một cây trong hình vẽ dưới đây :

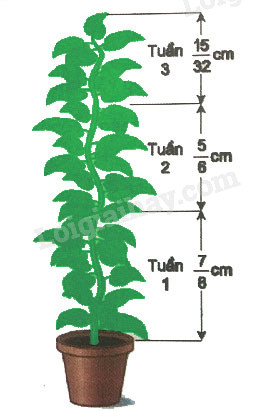
a) Ghi chép lại sự tăng trưởng của cây theo từng tuần.

b) Trả lời câu hỏi :

- Sau 3 tuần cây tăng trưởng được bao nhiêu xăng-ti-mét ?

- Tuần nào cây tăng trưởng nhanh nhất ?

Lời giải chi tiết

a) Sự tăng trưởng của cây từng tuần :

Tuần \(1\) : cây tăng trưởng được \(\dfrac{7}{8}cm\).

Tuần \(2\): cây tăng trưởng được \(\dfrac{5}{6}cm\).

Tuần \(3\): cây tăng trưởng được \(\dfrac{{15}}{{32}}cm\).

b) Sau \(3\) tuần, cây tăng trưởng được số xăng-ti-mét là : 

\(\dfrac{7}{8} + \dfrac{5}{6} + \dfrac{{15}}{{32}} = \dfrac{{209}}{{96}}\,\,(cm)\)

*) Để biết tuần nào cây tăng trưởng nhanh nhất ta sẽ so sánh các phân số \(\dfrac{7}{8}cm\,;\,\,\dfrac{5}{6}cm\) và \(\dfrac{{15}}{{32}}cm\).

Quy đồng mẫu số các phân số ta có :

\(\dfrac{7}{8} = \dfrac{{7 \times 12}}{{8 \times 12}} = \dfrac{{84}}{{96}}\) ;                \(\dfrac{5}{6} = \dfrac{{5 \times 16}}{{6 \times 16}} = \dfrac{{80}}{{96}}\) ;                \(\dfrac{{15}}{{32}} = \dfrac{{15 \times 3}}{{32 \times 3}} = \dfrac{{45}}{{96}}\)

Vì \(\dfrac{{84}}{{96}} > \dfrac{{80}}{{96}} > \dfrac{{45}}{{96}}\) nên \(\dfrac{7}{8} > \dfrac{5}{6} > \dfrac{{15}}{{32}}\).

Hay ta có : \(\dfrac{7}{8}cm > \dfrac{5}{6}cm > \dfrac{{15}}{{32}}cm\).

Vậy tuần \(1\) cây tăng trưởng nhanh nhất.