B. Hoạt động thực hành - Bài 6 : Hỗn số (tiếp theo)

Câu 1

Chuyển các hỗn số sau thành phân số :

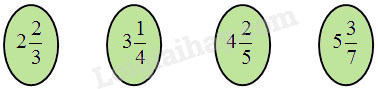
Phương pháp :

Có thể viết hỗn số thành một phân số có :

• Tử số bằng phần nguyên nhân với mẫu số rồi cộng với tử số ở phần phân số.

• Mẫu số bằng mẫu số ở phần phân số.

Cách giải :

\(2\dfrac{2}{3} = \dfrac{{2 \times 3 + 2}}{3} = \dfrac{8}{3}\) ;                                 \(3\dfrac{1}{4} = \dfrac{{3 \times 4 + 1}}{4} = \dfrac{{13}}{4}\)  ;

\(4\dfrac{2}{5} = \dfrac{{4 \times 5 + 2}}{5} = \dfrac{{22}}{5}\) ;                               \(5\dfrac{3}{7} = \dfrac{{5 \times 7 + 3}}{7} = \dfrac{{38}}{7}\).

Câu 2

Chuyển các hỗn số sau thành phân số thập phân : 

\(4\dfrac{3}{{10}}\,\);            \(21\dfrac{7}{{100}}\) ;          \(7\dfrac{{39}}{{100}}\) ;          \(6\dfrac{{123}}{{1000}}.\)

Phương pháp :

Có thể viết hỗn số thành một phân số có :

• Tử số bằng phần nguyên nhân với mẫu số rồi cộng với tử số ở phần phân số.

• Mẫu số bằng mẫu số ở phần phân số.

Lưu ý : Phân số thập phân là phân số có mẫu số là \(10\,;\,\,100\,;\,\,1000\,;\,\,...\)

Cách giải :

\(4\dfrac{3}{{10}}\, = \dfrac{{4 \times 10 + 3}}{{10}} = \dfrac{{43}}{{10}}\)  ;                         \(21\dfrac{7}{{100}} = \dfrac{{21 \times 100 + 7}}{{100}} = \dfrac{{2107}}{{100}}\)  ;

\(7\dfrac{{39}}{{100}} = \dfrac{{7 \times 100 + 39}}{{100}} = \dfrac{{739}}{{100}}\) ;                         \(6\dfrac{{123}}{{1000}} = \dfrac{{6 \times 1000 + 123}}{{1000}} = \dfrac{{6123}}{{1000}}\).

Câu 3

Chuyển các hỗn số sau thành phân số rồi thực hiện phép tình (theo mẫu) : 

a) \(5\dfrac{2}{{10}} + 7\dfrac{1}{{10}}\)                                          b) \(5\dfrac{6}{7} - 3\dfrac{5}{7}\)

c) \(8\dfrac{3}{5} \times 2\dfrac{6}{7}\)                                               d) \(1\dfrac{3}{{10}}:5\dfrac{7}{8}\)

Phương pháp :

Chuyển hỗn số thành phân số rồi thực hiện các phép tính cộng, trừ, nhân, chia hai phân số như thông thường.

Cách giải :

a) \(5\dfrac{2}{{10}} + 7\dfrac{1}{{10}} = \dfrac{{52}}{{10}} + \dfrac{{71}}{{10}} = \dfrac{{123}}{{10}};\)

b) \(5\dfrac{6}{7} - 3\dfrac{5}{7} = \dfrac{{41}}{7} - \dfrac{{26}}{7} = \dfrac{{15}}{7};\)

c) \(8\dfrac{3}{5} \times 2\dfrac{6}{7} = \dfrac{{43}}{5} \times \dfrac{{20}}{7} = \dfrac{{43 \times 20}}{{5 \times 7}}\)\( = \dfrac{{43 \times 5 \times 4}}{{5 \times 7}} = \dfrac{{172}}{7}.\)

d) \(1\dfrac{3}{{10}}:5\dfrac{7}{8} = \dfrac{{13}}{{10}}:\dfrac{{47}}{8} = \dfrac{{13}}{{10}} \times \dfrac{8}{{47}} \) \(= \dfrac{{13 \times 8}}{{10 \times 47}} = \dfrac{{13 \times 4 \times 2}}{{5 \times 2 \times 47}} = \dfrac{{52}}{{235}}.\)

Câu 4

So sánh các hỗn số :

a) \(7\dfrac{9}{{10}}\) và \(4\dfrac{9}{{10}}\) ;                                      b) \(6\dfrac{3}{{10}}\) và \(6\dfrac{5}{{9}}\).

 Chú ý : Khi so sánh hai hỗn số ta đưa về so sánh hai phân số tương ứng.

Phương pháp :

Chuyển hỗn số thành phân số rồi so sánh hai phân số như thông thường.

Cách giải :

a) Ta có : \(7\dfrac{9}{{10}} = \dfrac{{79}}{{10}}\,\,\,;\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,4\dfrac{9}{{10}} = \dfrac{{49}}{{10}}\)

Vì \(\dfrac{{79}}{{10}} > \dfrac{{49}}{{10}}\) nên \(7\dfrac{9}{{10}} > 4\dfrac{9}{{10}}.\)

b) Ta có : \(6\dfrac{3}{{10}} = \dfrac{{63}}{{10}}\,\,;\,\,\,\,\,\,\,  6\dfrac{5}{9} = \dfrac{{59}}{9}\)

Quy đồng mẫu số hai phân số \(\dfrac{{63}}{{10}}\) và \(\dfrac{{59}}{9}\) ta được :

\(\dfrac{{63}}{{10}} = \dfrac{{63 \times 9}}{{10 \times 9}} = \dfrac{{567}}{{90}}\,  \,\,;\)                          \(\dfrac{{59}}{9} = \dfrac{{59 \times 10}}{{9 \times 10}} = \dfrac{{590}}{{10}}\)

Vì \(\dfrac{{567}}{{10}} < \dfrac{{590}}{{10}}\) nên  \(\dfrac{{63}}{{10}} < \dfrac{{59}}{9}\).

Do đó : \(6\dfrac{3}{{10}} < 6\dfrac{5}{9}\).

Câu 5

Đúng ghi Đ, sai ghi S :

a) \(5\dfrac{5}{8} = \dfrac{{33}}{8}\)                                              b) \(6\dfrac{3}{4} = \dfrac{{27}}{4}\)

c) \(6\dfrac{3}{4} = \dfrac{{27}}{4}\)                                              d) \(7\dfrac{5}{6} = \dfrac{{29}}{6}\)

Phương pháp :

- Chuyển hỗn số thành phân số sau đó xác định tính đúng – sai của mỗi khẳng định.

- Có thể viết hỗn số thành một phân số có :

• Tử số bằng phần nguyên nhân với mẫu số rồi cộng với tử số ở phần phân số.

• Mẫu số bằng mẫu số ở phần phân số.

Cách giải :

a) \(5\dfrac{5}{8} = \dfrac{{5 \times 8 + 5}}{8} = \dfrac{{45}}{8}\). Do đó, khẳng định \(5\dfrac{5}{8} = \dfrac{{33}}{8}\) là sai.

b) \(11\dfrac{3}{8} = \dfrac{{11 \times 8 + 3}}{8} = \dfrac{{91}}{8}\). Do đó, khẳng định \(11\dfrac{3}{8} = \dfrac{{91}}{8}\)là đúng.

c) \(6\dfrac{3}{4} = \dfrac{{6 \times 4 + 3}}{4} = \dfrac{{27}}{4}\). Do đó, khẳng định \(6\dfrac{3}{4} = \dfrac{{27}}{4}\) là đúng.

d) \(7\dfrac{5}{6} = \dfrac{{7 \times 6 + 5}}{6} = \dfrac{{47}}{6}\). Do đó, khẳng định \(7\dfrac{5}{6} = \dfrac{{29}}{6}\) là sai.