B. Hoạt động thực hành - Bài 37 : Nhân một số thập phân với một số thập phân

Câu 1

Đặt tính rồi tính :

a) 25,8 × 1,5                                              b) 13,25 × 6,7

c) 0,24 × 4,7                                              d) 7,826 × 4, 5

Phương pháp giải :

- Thực hiện phép nhân như nhân các số tự nhiên.

- Đếm xem trong phần thập phân của cả hai thừa số có bao nhiêu chữ số rồi dùng dấu phẩy tách ở tích ra bấy nhiêu chữ số kể từ phải sang trái.

Cách giải :

---

Câu 2

a) Tính rồi so sánh giá trị của \(a\times b\) và \(b \times a\) :

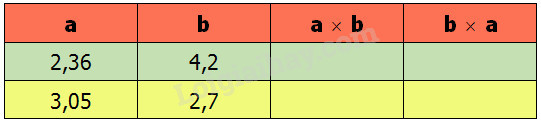
b) Em và bạn đọc rồi giải thích cho nhau nội dung sau :

Nhận xét :

Phép nhân các số thập phân có tính chất giao hoán : Khi đổi chỗ hai thừa số của một tích thì tích không thay đổi.

 c) Viết ngay kết quả tính :

Phương pháp giải :

a) Thực hiện phép nhân các số rồi so sánh.

b) Đọc hiểu nội dung trong phần đóng khung.

c) Vận dụng kiến thức về tính chất giao hoán, quan sát rồi điền kết quả vào chỗ chấm.

Cách giải :

a) 

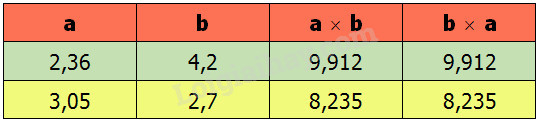
b) Học sinh tự đọc.

c) Viết ngay kết quả tính:

---

Câu 3

Thực hiện lần lượt các hoạt động sau:

a) Đặt tính rồi tính:

    142,57 × 0,1                                                531,75 × 0,01

b) Em và bạn đọc rồi giải thích cho nhau nội dung sau :

c)  Tính nhẩm:

Phương pháp giải :

a) Đặt tính rồi tính theo cách thực hiện phép nhân số thập phân với số thập phân.

b) Đọc nội dung phần đóng khung.

c) Vận dụng kiến thức về phép nhân trong quy tắc phần b; tính nhẩm rồi điền kết quả vào chỗ trống.

Cách giải :

a)

\(\dfrac{{ \times \begin{array}{*{20}{r}}{142,57}\\{0,1}\end{array}}}{{\begin{array}{*{20}{r}}{14257}\\{00000\,\,\,}\\\hline{14,257}\end{array}}}\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\,\dfrac{{ \times \begin{array}{*{20}{r}}{531,75}\\{0,01}\end{array}}}{{\begin{array}{*{20}{r}}{\,\,\,\,53175}\\\begin{array}{l}00000\,\,\\00000\,\,\,\end{array}\\\hline{5,3175}\end{array}}}\)

b) Đọc nội dung phần đóng khung.

c) Tính nhẩm:

---

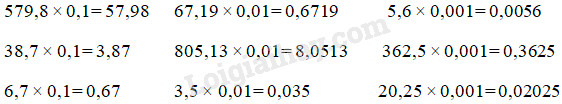
Câu 4

Viết các số đo sau dưới dạng số đo có đơn vị là ki-lô-mét vuông : 

a) 1000ha                                b) 125ha

c) 57,4ha                                 d) 3,2ha.

Phương pháp giải :

- Nhớ lại kiến thức : \(1k{m^2} = 100ha;\) \(1ha = \dfrac{1}{{100}} = 0,01k{m^2}.\)

- Vận dụng quy tắc phép nhân số thập phân với \(0,01\) rồi đổi các số đo theo yêu cầu.

Cách giải :

\({a)\,\,1000ha = {\rm{ }}10k{m^2}}\)

\({b)\,\,125ha{\rm{ }} = {\rm{ }}1,25k{m^2}}\)

\({c)\;{\rm{ }}57,4ha = {\rm{ }}0,574k{m^2}}\) 

\({d)\;{\rm{ }}3,2ha{\rm{ }} = {\rm{ }}0,032k{m^2}}\)

---

Câu 5

Giải bài toán sau: Một vườn cây hình chữ nhật có chiều dài 15,62m và chiều rộng 8,4m. Tính chu vi và diện tích vườn cây đó.

Phương pháp giải :

- Chu vi hình chữ nhật bằng chiều dài cộng chiều rộng (cùng đơn vị đo) rồi nhân với 2.

- Diện tích hình chữ nhật bằng chiều dài nhân với chiều rộng (cùng đơn vị đo).

Cách giải :

Chu vi của vườn cây hình chữ nhật là:

         (15,62 + 8,4) × 2 = 48,04 (m)

Diện tích của vườn cây hình chữ nhật là:

         15,62 × 8,4 = 131,208 (\({m^2}\))

         Đáp số: Chu vi: 48,04 m

                       Diện tích: 131,208 \({m^2}\).

---

Câu 6

Giải bài toán sau: Trên bản đồ tỉ lệ 1: 1000000, quãng đường từ Thành phố Hồ Chí Minh đến Phan Thiết đo được là 19,8cm. Hỏi độ dài thật của quãng đường từ Thành phố Hồ Chí Minh đến Phan Thiết là bao nhiêu ki-lô-mét ?

Phương pháp giải :

- Nhớ lại kiến thức về tỉ lệ bản đồ.

- Vận dụng kiến thức về phép nhân số thập phân rồi tìm kết quả cho bài toán.

Cách giải :

Tỉ lệ 1: 1 000 000 nghĩa là trên bản đồ 1cm ứng với 1000 000 cm độ dài thực tế.

Vậy quãng đường từ Thành phố Hồ Chí Minh đến Phan Thiết dài số ki-lô-mét là :

         19,8 × 1 000 000 = 19 800 000 (cm)

         19 800 000cm = 198km

                            Đáp số: 198km.