A. Hoạt động thực hành - Bài 116 : Em ôn lại những gì đã học

Câu 1

Xếp nhanh các thẻ dưới đây thành phép tính đúng.

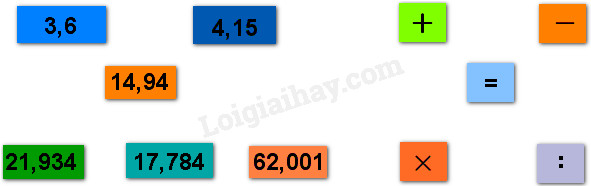
Phương pháp giải:

Nhẩm tính giá trị các phép tính ra nháp rồi xếp các thẻ đã cho thành phép tính đúng.

Lời giải chi tiết:

Ví dụ :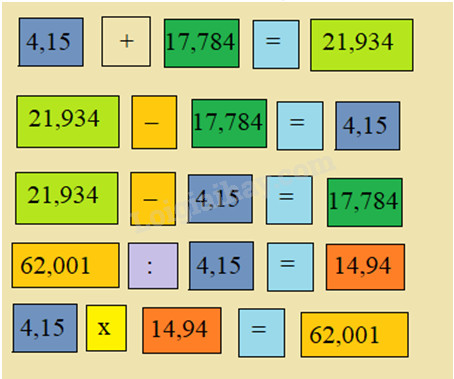

Ngoài những phép tính trên còn có nhiều các phép tính khác, các em tự tìm tiếp nhé.

Câu 2

Tính :

a) \(85793  –  36841 + 3836 \)

b) \(\dfrac{{84}}{{100}} - \dfrac{{29}}{{100}} + \dfrac{{30}}{{100}}\)

c) \(325,97 + 86,54 + 103,46\)

Phương pháp giải:

Biểu thức chỉ có phép cộng và phép trừ thì ta tính lần lượt từ trái sang phải.

Lời giải chi tiết:

Câu 3

 Tìm \(x\) :

 \(a)\;x+ 28 = 4,72 + 2,28\)                         \( b)\;x– 7,2 = 3,9 + 2,7\)

Phương pháp giải:

- Tính giá trị vế phải.

- Tìm \(x\) dựa vào các quy tắc đã học:

+ Muốn tìm số hạng chưa biết ta lấy tổng trừ đi số hạng đã biết.

+ Muốn tìm số bị trừ ta lấy hiệu cộng với số trừ. 

Lời giải chi tiết:

Câu 4

Một mảnh đất hình thang có đáy bé là 150m, đáy lớn bằng \(\dfrac{5}{3}\) đáy bé, chiều cao bằng \(\dfrac{2}{5}\) đáy lớn. Hỏi diện tích mảnh đất bằng bao nhiêu mét vuông, bao nhiêu héc-ta ?

Phương pháp giải:

- Tính đáy lớn = đáy bé × \(\dfrac{5}{3}\).

- Tính chiều cao = đáy lớn × \(\dfrac{2}{5}\).

- Tính diện tích = (đáy lớn \(+\) đáy bé) × chiều cao \(:2\).

- Đổi số đo diện tích sang đơn vị héc-ta, lưu ý rằng \(1ha =10000m^2\).

Lời giải chi tiết:

Đáy lớn của mảnh đất hình thang là :

             150 × \(\dfrac{5}{3}\) = 250 (m)

Chiều cao của mảnh đất hình thang là :

            250 × \(\dfrac{2}{5}\) = 100 (m)

Diện tích mảnh đất hình thang là :

          (150 + 250) × 100 : 2 = 20000 (m²)

           20 000m²  = 2ha

                        Đáp số : 20 000m² ;  2ha.

Câu 5

 Đoạn đường AB dài 279km. Lúc 7 giờ, một ô tô chở hàng đi từ A với vận tốc 45km/giờ. Đến 8 giờ một ô tô du lịch cũng đi từ A với vận tốc 60km/giờ và đi cùng chiều với ô tô chở hàng. Hỏi đến mấy giờ ô tô du lịch đuổi kịp ô tô chở hàng ? 

Phương pháp giải:

Hai xe chuyển động cùng chiều và xuất phát không cùng lúc. Để giải bài toán này ta có thể làm như sau:

Bước 1: Tính thời gian ô tô chở hàng chở hàng đi trước ô tô du lịch : 8 giờ – 7 giờ = 1 giờ.

Bước 2: Tính số ki-lô-mét ô tô chở hàng đi trước ô tô du lịch (chính là quãng đường ô tô chở hàng đi được trong 1 giờ).

Bước 3: Tính số ki-lô-mét mà mỗi giờ ô tô du lịch gần ô tô chở hàng.

Bước 4: Tính thời gian đi để ô tô du lịch đuổi kịp ô tô chở hàng = số ki-lô-mét ô tô chở hàng đi trước ô tô du lịch \(:\) số ki-lô-mét mà mỗi giờ ô tô du lịch gần ô tô chở hàng.

Bước 5: Thời gian lúc ô tô du lịch đuổi kịp ô tô chở hàng = thời gian lúc ô tô du lịch xuất phát + thời gian đi để ô tô du lịch đuổi kịp ô tô chở hàng.

Lời giải chi tiết:

Ô tô chở hàng đi trước ô tô du lịch số giờ là :

            8 giờ – 7 giờ = 1 giờ

Sau 1 giờ, ô tô chở hàng đi được số ki-lô-mét là :

            45 × 1 = 45 (km)

Sau mỗi giờ ô tô du lịch gần ô tô chở hàng số ki-lô-mét là :

            60 – 45 = 15 (km)

Thời gian để ô tô du lịch đuổi kịp ô tô chở hàng là :

            45 : 15 = 3 (giờ)

Ô tô du lịch đuổi kịp ô tô chở hàng lúc :

             8 giờ + 3 giờ = 11 giờ

                         Đáp số: 11 giờ.

Câu 6

Tìm \(x\) :        \(\dfrac{4}{x} = \dfrac{1}{5}\)

Phương pháp giải:

Áp dụng tính chất cơ bản của phân số: Nếu nhân cả tử số và mẫu số của một phân số với cùng một số tự nhiên khác \(0\) thì được một phân số bằng phân số đã cho.

Lời giải chi tiết:

Ta có: \(\dfrac{1}{5}= \dfrac{1 \times 4}{5 \times 4} = \dfrac{4}{20}\) 

Do đó: \(\dfrac{4}{x}= \dfrac{4}{20}\).

Suy ra: \(x = 20\) (Hai phân số bằng nhau có tử số bằng nhau thì mẫu số cũng bằng nhau).

Câu 7

Tính :

Phương pháp giải:

- Đặt tính rồi tính theo các quy tắc đã học về phép nhân hoặc phép chia số thập phân.

- Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.

- Muốn chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược.

Lời giải chi tiết:

Câu 8

Tìm \(x\) :

Phương pháp giải:

Áp dụng các quy tắc:

- Muốn tìm thừa số chưa biết ta lấy tích chia cho thừa số đã biết.

- Muốn tìm số bị chia ta lấy thương nhân với số chia.

- Muốn tìm số chia ta lấy số bị chia chia cho thương. 

Lời giải chi tiết:

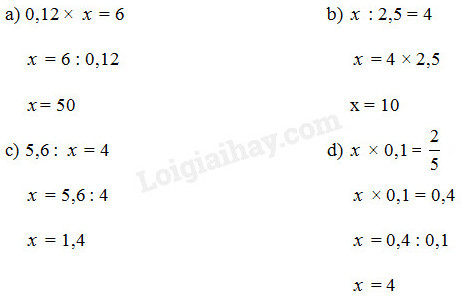
Câu 9

Trong ba ngày một cửa hàng bán được 2400kg đường. Ngày thứ nhất bán được 35% số đường đó, ngày thứ hai bán được 40% số đường ban đầu. Hỏi ngày thứ ba bán được bao nhiêu ki-lô-gam đường ?

Phương pháp giải:

- Tìm số đường bán ngày thứ nhất, ngày thứ hai theo quy tắc:

Muốn tìm a% của B ta có thể lấy B chia cho 100 rồi nhân với a hoặc lấy B  nhân với a rồi chia cho 100.

- Số đường bán ngày thứ ba = số đường bán trong ba ngày \(-\) số đường bán ngày thứ nhất \(-\) số đường bán ngày thứ hai. 

Lời giải chi tiết:

Cách 1:

Cả hai ngày bán được số đường là :

            35% + 40% = 75 % (số đường) 

Trong hai ngày đầu cửa hàng bán được số ki-lô-gam đường là :

            2400 : 100 × 75 = 1800 (kg)

Ngày thứ ba cửa hàng bán được số ki-lô-gam đường là :

            2400  – 1800 = 600 (kg)

                                    Đáp số: 600kg.

Cách 2:

Ngày thứ nhất cửa hàng bán được số ki-lô-gam đường là :

            2400 : 100 × 35 = 840 (kg)

Ngày thứ hai cửa hàng bán được số ki-lô-gam đường là :

            2400 : 100 × 40 =  960 (kg)

Ngày thứ ba cửa hàng bán được số ki-lô-gam đường là :

            2400 – (960 + 840) = 600 (kg)

                                    Đáp số: 600kg.

Câu 10

Một cửa hàng bán hoa quả thu được 1 800 000 đồng. Tính ra số tiền lãi bằng 20% tiền vốn. Hỏi tiền vốn để mua số hoa quả đó là bao nhiêu đồng ?

Phương pháp giải:

Áp dụng công thức:  tiền bán = tiến vốn + tiền lãi. 

Lời giải chi tiết:

Coi số tiền vốn để mua số hoa quả đó là 100%.

Tiền bán hoa quả chiếm số phần trăm so với tiền vốn là :

            100% + 20% = 120% tiền vốn

Số tiền vốn để mua số hoa quả đó là :

   1 800 000 : 120 × 100  = 1 500 000 (đồng)

                    Đáp số: 1 500 000 đồng.