A. Hoạt động thực hành - Bài 105 : Ôn tập về phép nhân, phép chia

Câu 1, 2

Câu 1 (trang 115 toán VNEN lớp 5 tập 2)

a) Đọc kĩ nội dung sau :

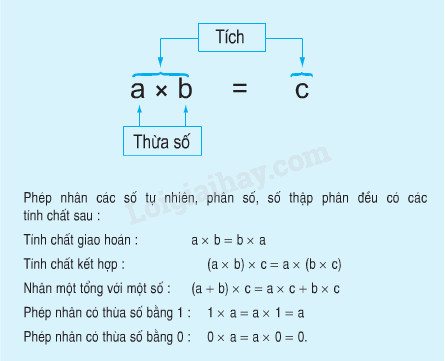
b) Lấy một ví dụ minh họa rồi giải thích cho bạn nghe.

Phương pháp :

Em đọc kĩ nội dung trong phần a) rồi tự lấy các ví dụ minh họa.

Cách giải :

Ví dụ:

• Tính chất giao hoán :  4 × 5 = 5 × 4 = 20.

• Tính chất kết hợp :

  (3 × 25) × 4 =  3 × (25 × 4) = 300.

• Nhân một tổng với một số :

  (37 + 63) × 15 = 37 × 15 + 63 × 15.

• Phép nhân có thừa số bằng 1 :

  1 × 2019 = 2019  × 1 = 2019.

• Phép nhân có thừa số bằng 0 :

  9999 × 0 = 0 × 9999 = 0.

 Câu 2 (trang 115 toán VNEN lớp 5 tập 2)

Tính :

Phương pháp :

- Muốn nhân hai số tự nhiên ta đặt tính rồi tính sao cho các chữ số ở cùng một hàng thì thẳng cột với nhau, sau đó nhân theo thứ tự từ phải sang trái.

- Muốn nhân hai phân số ta lấy tử số nhân với tử số, mẫu số nhân với mẫu số.

- Muốn nhân hai số thập phân ta đặt tính rồi nhân như nhân các số tự nhiên, sau đó đếm ×em trong phần thập phân của cả hai thừa số có bao nhiêu chữ số rồi dùng dấu phẩy tách ở tích ra bấy nhiêu chữ số kể từ phải sang trái.

Cách giải :

---

Câu 3, 4

 Câu 3 (trang 115 toán VNEN lớp 5 tập 2)

Tính nhẩm :

Phương pháp :

- Muốn nhân một số thập phân với 10, 100, 1000, ... ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên phải một, hai, ba, ... chữ số.

- Muốn nhân một số thập phân với 0,1; 0,01; 0,001; ... ta chỉ việc chuyển dấu phẩy của số đó lần lượt sang bên trái một, hai, ba, ... chữ số. 

Cách giải :

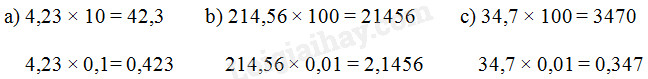
 Câu 4 (trang 115 toán VNEN lớp 5 tập 2)

Tính bằng cách thuận tiện nhất

Phương pháp :

Áp dụng các tính chất của phép nhân như :

Tính chất giao hoán:    a × b =  b × a

Tính chất kết hợp:

       (a × b) × c = a × (b × c)

Nhân một tổng với một số:

      (a + b) × c = a × c + b × c.

Cách giải :

---

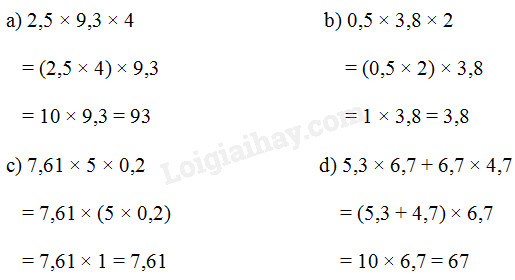
Câu 5, 6

 Câu 5 (trang 115 toán VNEN lớp 5 tập 2)

Một ô tô và xe máy khởi hành cùng một lúc và đi ngược chiều nhau. Ô tô đi từ A với vận tôc 48,5 km/giờ, xe máy đi từ B với vận tốc 33,5 km/giờ. Sau 1 giờ 30 phút ô tô và xe máy gặp nhau tại C. Hỏi quãng đường AB dài bao nhiêu ki-lô-mét?

Phương pháp :

- Đổi : 1 giờ 30 phút = 1,5 giờ.

- Tính quãng đường ô tô đi từ A đi được trong 1,5 giờ ta lấy vận tốc nhân với thời gian.

- Tính quãng đường xe máy đi từ B đi được trong 1,5 giờ ta lấy vận tốc nhân với thời gian.

- Vì hai xe khởi hành cùng lúc và đi ngược chiều nhau nên để tính quãng đường AB ta lấy quãng đường ô tô đi từ A đi được trong 1,5 giờ cộng với quãng đường xe máy đi từ B đi được trong 1,5 giờ.

Cách giải :

Đổi: 1 giờ 30 phút = 1,5 giờ

Quãng đường xe máy đi được trong 1,5 giờ là : 

            33,5 × 1,5 = 50,25 (km)

Quãng đường ô tô đi được trong 1,5 giờ là:  

            48,5 × 1,5 = 72,75 (km)

Vậy đoạn đường AB dài số ki-lô-mét là:

             50,25 + 72,75 = 123 (km)

                                    Đáp số: 123km.

 Câu 6 :

a) Đọc kĩ nội dung sau :

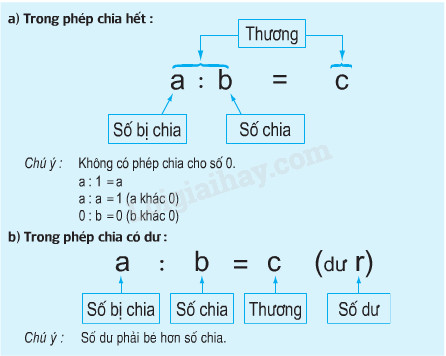
b) Lấy ví dụ minh họa rồi giải thích cho bạn nghe.

Phương pháp :

Em đọc kĩ nội dung trong phần a) rồi tự lấy các ví dụ minh họa.

Cách giải :

b) Ví dụ :

• 99 : 1 = 99 (Vì số nào chia cho 1 cũng bằng chính số đó).

• 2019 : 2019 = 1 (Vì số nào chia cho chính số đó cũng bằng 1).

• 0 : 1234 = 0 (Vì 0 chia cho số bất kì (khác 0) thì đều bằng 0).

---

Câu 7, 8

Câu 7 (trang 116 toán VNEN lớp 5 tập 2)

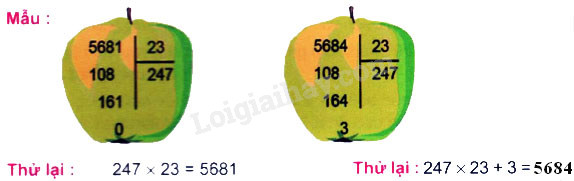
Tính rồi thử lại theo mẫu:

a) 3675 : 35                             20219 : 37

b) 81,92 : 32                            97,65 : 21,7 (thương là số thập phân)

Chú ý :

Phép chia hết : \(a:b = c\), ta có  :  \(a = c \times b\) (\(b\) khác \(0\)).

Phép chia có dư : \(a:b = c\) (dư \(r\)), ta có  \(a = c \times b + r\) (\(0 < r < b\)).

Phương pháp :

Ta đặt tính theo cột dọc, sau đó chia theo thứ tự từ trái sang phải.

Cách giải :

 

 Câu 8 (trang 116 toán VNEN lớp 5 tập 2)

Tính :

Phương pháp :

Để chia hai phân số ta lấy phân số thứ nhất nhân với phân số thứ hai đảo ngược:

                  \( \dfrac{a}{b} :\dfrac{c}{d} = \dfrac{a}{b} \times \dfrac{d}{c}\).

Cách giải :

a) \(\dfrac{3}{8}:\dfrac{5}{4} = \dfrac{3}{8} \times \dfrac{4}{5} = \dfrac{{3 \times 4}}{{8 \times 5}}\)\( = \dfrac{{3 \times 4}}{{4 \times 2 \times 5}} = \dfrac{3}{{10}}\)

b) \(\dfrac{4}{7}:\dfrac{2}{{13}} = \dfrac{4}{7} \times \dfrac{{13}}{2} = \dfrac{{4 \times 13}}{{7 \times 2}}\)\( = \dfrac{{2 \times 2 \times 13}}{{7 \times 2}} = \dfrac{{26}}{7}\)

---

Câu 9, 10

Câu 9 (trang 117 toán VNEN lớp 5 tập 2)

Tính nhẩm :

Phương pháp :

- Muốn chia một số tự nhiên cho 0,1,; 0,01; 0,001; ... ta chỉ việc thêm vào bên phải số đó một, hai, ba, ... chữ số 0.

- Muốn nhân một số tự nhiên với 10; 100; 1000;  ... ta chỉ việc thêm vào bên phải số đó một, hai, ba, ... chữ số 0.

- Muốn chia một số cho 0,25 ta chỉ việc nhân số đó với 4.

-  Muốn chia một số cho 0,5 ta chỉ việc nhân số đó với 2.

Cách giải :

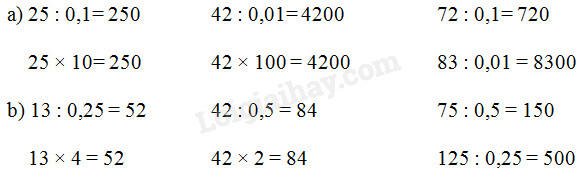
Câu 10 (trang 117 toán VNEN lớp 5 tập 2)

Cuối năm 2013, số dân của nước ta là 90 000 000 người. Nếu tỉ lệ tăng dân số hằng năm là 1,2% thì hết năm 2014 số dân của nước ta là bao nhiêu người ?

Phương pháp :

- Tính số người tăng thêm ta lấy số dân cuối năm 2013 chia cho 100 rồi nhân với 1,2.

- Số dân cuối năm 2014 = số dân cuối năm 2013 + số người tăng thêm.  

Cách giải :

Nếu tỉ lệ tăng dân số hằng năm là 1,2% thì  năm 2014 nước ta tăng thêm số dân là :

90 000 000 : 100 × 1,2 = 1 080 000 (người)

Dân số nước ta đến hết năm 2014 là :

   90 000 000 + 1 080 000 = 91 080 000 (người)

                         Đáp số: 91 080 000 người.