A. Hoạt động cơ bản - Bài 24 : So sánh hai số thập phân

Câu 1

Thực hành lần lượt các hoạt động sau:

- Quan sát hình vẽ dưới đây:

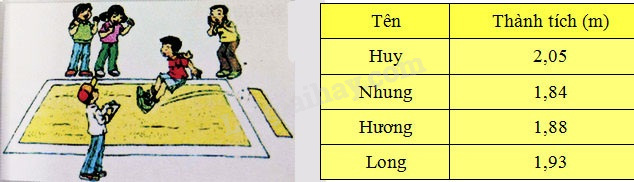
- Đọc bảng ghi thành tích nhảy xa của các bạn trong nhóm

- Thảo luận xem bạn nào nhảy xa hơn bạn nào ? Tại sao ? 

Phương pháp :

- Quan sát bảng đã cho rồi đọc bảng ghi thành tích của các bạn. Muốn đọc một số thập phân, ta đọc lần lượt từ hàng cao đến hàng thấp : trước hết đọc phần nguyên, đọc dấu "phẩy", sau đó đọc phần thập phân rồi đọc thêm tên đơn vị đo (nếu có).

Cách giải :

- Quan sát bảng em thấy :

+ Bạn Huy nhảy xa được 2,05m.

+ Bạn Nhung nhảy xa được 1,84m.

+ Bạn Hương nhảy xa được 1,88m.

+ Bạn Long nhảy xa được 1,93m.

- Bạn nhảy xa nhất là bạn Huy (2,05m) vì đó là thành tích cao nhất trong lớp.

Câu 2

a) Thực hiện lần lượt các hoạt động sau :

- Lấy hai băng giấy đã chia thành 10 phần bằng nhau.

- Tô màu vào 3 phần của băng giấy thứ nhất và 7 phần vào băng giấy thứ hai.

- Viết số thập phân chỉ phần đã tô màu của mỗi băng giấy trên.

- So sánh phần đã tô màu của hai băng giấy và rút ra nhận xét.

Phương pháp :

- Quan sát hình vẽ để viết phân số và số thập phân chỉ phần đã tô màu của mỗi hình.

- So sánh hai phân số rồi từ đó so sánh phần đã tô màu của mỗi băng giấy.

Cách giải :

Số thập phân chỉ phần đã tô màu của băng giấy thứ nhất là \(\dfrac{3}{{10}} = 0,3\).

Số thập phân chỉ phần đã tô màu của băng giấy thứ hai là \(\dfrac{7}{{10}} = 0,7\).

Ta có : \(\dfrac{7}{{10}} > \dfrac{3}{{10}}.\)  Vậy \(0,7 > 0,3.\)

b) Đọc kĩ nội dung sau :

Câu 3

Đọc kĩ nội dung sau và giải thích cho bạn nghe :

a) Ví dụ 1 : So sánh 7,2 và 6,9.

Ta có thể viết : \(7,2 = \dfrac{{72}}{{10}}\,\,\,  ;  6,9 = \dfrac{{69}}{{10}}.\)

Ta có : \(\dfrac{{72}}{{10}} > \dfrac{{69}}{{10}}\) (72 > 69 vì ở hàng chục có 7 > 6).

Vậy : 7,2 > 6,9 (phần nguyên có 7 > 6).

Trong hai số thập phân có phần nguyên khác nhau, số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn.

b) Ví dụ 2 : So sánh : 35,7 và 35,698.

Ta thấy 35,7 và 35,698 đều có phần nguyên bằng nhau (đều bằng 35), ta so sánh các phần thập phân :

Phần thập phân của 35,7 là \(\dfrac{7}{{10}}.\)

Phần thập phân của 35,698 là \(\dfrac{{698}}{{1000}}.\)

Mà \(\dfrac{7}{{10}} = \dfrac{{700}}{{1000}}\,;\,\,\dfrac{{700}}{{1000}} > \dfrac{{698}}{{1000}}\,\) (700 > 698 vì ở hàng phần trăm có 7 > 6).

Vậy \(\dfrac{7}{{10}} > \dfrac{{698}}{{1000}}.\)

Do đó:  35,7 > 35,698 (phần nguyên bằng nhau, phần phần mười có 7 > 6).

Trong hai số thập phân có phần nguyên bằng nhau, số thập phân nào có hàng phần mười lớn hơn thì số đó lớn hơn.

c) Muốn so sánh hai số thập phân ta có thể làm như sau:

- So sánh các phần nguyên của hai số thập phân đó như so sánh hai số tự nhiên, số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn.

Ví dụ: 2012,5  > 1998,7 (vì 2012 > 1998).

- Nếu phần nguyên của hai số thập phân đó bằng nhau thì so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn, ... ; đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn.

 Ví dụ : 74,885 < 74,9 (vì phần nguyên bằng nhau, ở hàng phần mười có 8 < 9).

 430,72 > 430,70 (vì phần nguyên bằng nhau, hàng phần mười bằng nhau, ở hàng phần trăm có 2 > 0).

- Nếu phần nguyên và phần thập phân của hai số đó bằng nhau thì hai số đó bằng nhau.

Câu 4

So sánh hai số thập phân :

a) 3,05 và 2,84                                          b) 4,723 và 4,79

Phương pháp :

- So sánh các phần nguyên của hai số thập phân đó như so sánh hai số tự nhiên, số thập phân nào có phần nguyên lớn hơn thì số đó lớn hơn.

- Nếu phần nguyên của hai số thập phân đó bằng nhau thì ta so sánh phần thập phân, lần lượt từ hàng phần mười, hàng phần trăm, hàng phần nghìn ... đến cùng một hàng nào đó, số thập phân nào có chữ số ở hàng tương ứng lớn hơn thì số đó lớn hơn.

- Nếu phần nguyên và phần thập phân của hai số đó bằng nhau thì hai số đó bằng nhau.

Cách giải :

a) 3,05 > 2,84 (vì 3 > 2).         

b) 4,723 < 4,79 (vì phần nguyên bằng nhau, hàng phần mười bằng nhau, ở hàng phần trăm có 2 < 9).