Giải Hoạt động 1 trang 92, 93 SGK Toán 10 tập 2 - Chân trời sáng tạo
Vẽ các elip sau Thiết kế một đường hầm có mặt cắt hình nửa elip cao 4 m, rộng 10 m
Thực hành 1
Vẽ các elip sau
a) \(\frac{{{x^2}}}{{10}} + \frac{{{y^2}}}{4} = 1\)
b) \(\frac{{{x^2}}}{{12}} + \frac{{{y^2}}}{3} = 1\)
c) \(\frac{{{x^2}}}{{100}} + \frac{{{y^2}}}{{36}} = 1\)
Phương pháp giải:
Bước 1: Khởi động phần mềm Geogebra
Bước 2: Nhập phương trình elip \(\frac{{{x^2}}}{{{a^2}}} + \frac{{{y^2}}}{{{b^2}}} = 1\) theo cú pháp x^2/a^2 + y^2/b^2 = 1 vào vùng nhập lệnh
Bước 3: Quan sát hình vẽ xuất hiện trên vùng làm việc
Lời giải chi tiết:
Thực hiện các bước đã nêu ở phương pháp ta có
a) Nhập phương trình elip theo cú pháp x^2/10 + y^2/4 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
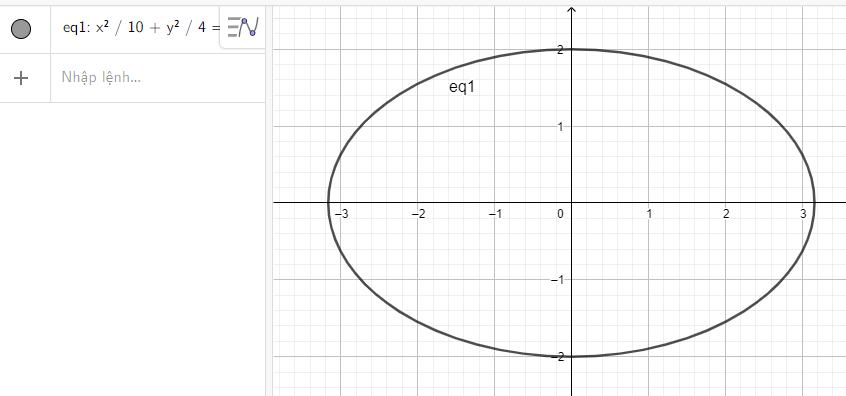
b) Nhập phương trình elip theo cú pháp x^2/12 + y^2/3 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
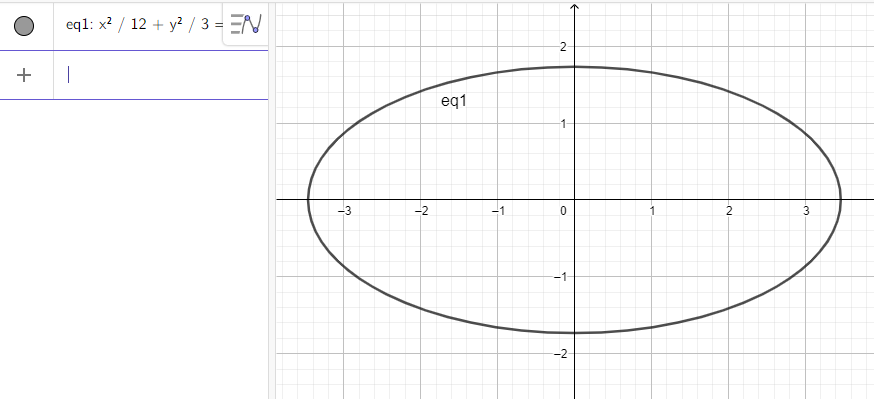
c) Nhập phương trình elip theo cú pháp x^2/100 + y^2/36 = 1 vào vùng nhập lệnh ta được hình elip dưới đây:
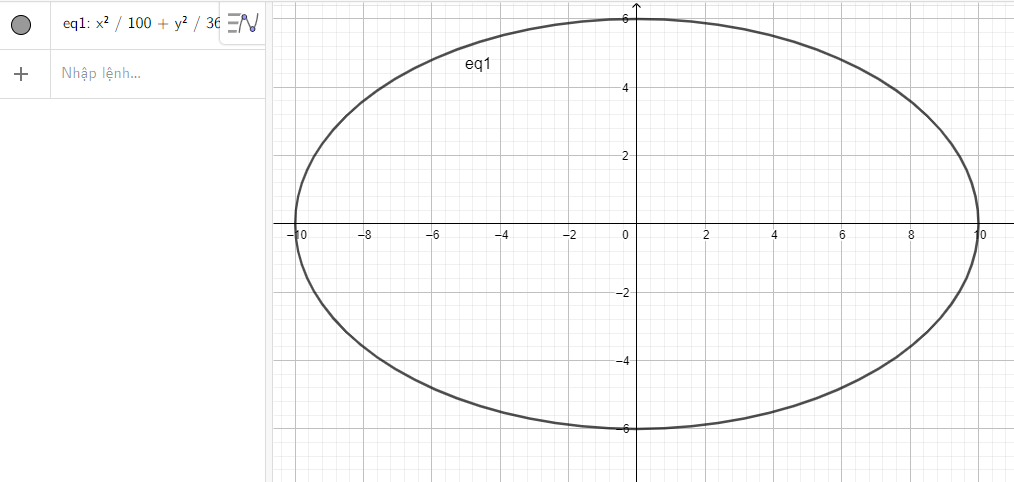
Thực hành 2
Thiết kế một đường hầm có mặt cắt hình nửa elip cao 4 m, rộng 10 m
Phương pháp giải:
Từ chiều rộng và chiều cao xác định a, b. Từ đó xác định công thức elip và hình dạng
Lời giải chi tiết:
Ta có: Chiều cao và chiều rộng của đường hầm là 4m, 10m nên ta có: \(a = 5,b = 4\)
Nên phương trình chính tắc của elip có dạng \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\)
Nhập phương trình elip theo cú pháp x^2/25 + y^2/16 = 1 {y>=0} vào vùng nhập lệnh ta có hình vẽ mô phỏng đường hầm dưới đây
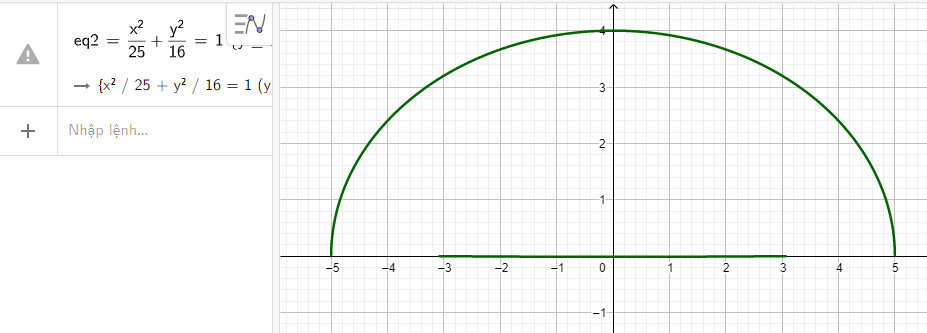
Vậy phương trình mô phỏng đường hầm là \(\frac{{{x^2}}}{{25}} + \frac{{{y^2}}}{{16}} = 1\) với \(y \ge 0\)
Và có hình mô phỏng thực tế như hình trên
Search google: "từ khóa + timdapan.com" Ví dụ: "Giải Hoạt động 1 trang 92, 93 SGK Toán 10 tập 2 - Chân trời sáng tạo timdapan.com"







