Đề thi học kì 2 toán lớp 9 năm 2019 - 2020 PGD quận Thanh Xuân

Đề bài

Bài 1  (2,0 điểm):

Cho hai biểu thức \(A = \dfrac{{\sqrt x  + 1}}{{\sqrt x }}\) và \(B = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x  - 2}} + \dfrac{1}{{\sqrt x  + 2}}\) với \(x \ge 0;x \ne 4.\)

1. Tính giá trị của biểu thức \(A\) khi \(x = 16.\)

2. Rút gọn biểu thức \(B.\)

3. Tìm tất cả các giá trị của \(x\) để \(AB = \dfrac{{\sqrt x  - 1}}{2}.\)

Bài 2 (2,5 điểm):

1. Giải bài toán bằng cách lập hệ phương trình hoặc lập phương trình.

Một phân xưởng theo kế hoạch phải sản xuất 630 sản phẩm trong một số ngày quy định. Do mỗi ngày phân xưởng đó sản xuất vượt mức 5 sản phẩm nên phân xưởng hoàn thành kế hoạch sớm hơn thời gian quy định là 3 ngày. Hỏi theo kế hoạch, mỗi ngày phân xưởng phải sản xuất được bao nhiêu sản phẩm?

2. Một lọ hoa hình trụ có đường kính đáy là 12cm, người ta đổ vào trong lọ một lượng nước với chiều cao của cột nước là 20cm. Tính thể tích nước trong lọ hoa.

Bài 3 (2,0 điểm):

1) Giải phương trình: \(\left\{ \begin{array}{l}\dfrac{1}{{x + 3}} - \dfrac{2}{{y - 1}} = 9\\\dfrac{3}{{x + 3}} + \dfrac{1}{{y - 1}} = 6\end{array} \right.\)

2) Cho phương trình \({x^2} + mx + m - 1 = 0\) (1) với \(x\) là ẩn số và \(m\) là tham số.

a) Giải phương trình khi \(m = 2.\)

b) Tìm tất cả các giá trị của \(m\) để phương trình có hai nghiệm \({x_1};{x_2}\) sao cho \({x_1} = 2{x_2}\).

Bài 4 (3,0 điểm):

Cho đường tròn \(\left( O \right)\) và một điểm A nằm ngoài đường tròn. Kẻ hai tiếp tuyến AB và AC với đường tròn (O), (B, C là tiếp điểm). Trên đoạn OB lấy điểm I (I khác B, I khác O). Đường thẳng AI cắt đường tròn (O) tại hai điểm D và E (D nằm giữa A và E)

1. Chứng minh rằng tứ giác ABOC nội tiếp

2. Chứng minh \(A{B^2} = AD.AE\)

3. Gọi H là giao điểm của \(BC\) và \(AO.\) Chứng minh rằng \(\widehat {AHD} = \widehat {AEO}\).

Bài 5 (0,5 điểm): 

Giải phương trình \(\sqrt {x - 2}  + \sqrt {4 - x}  = {x^2} - 6x + 11\)

HẾT

---

LG bài 1

Phương pháp giải:

1. Thay \(x = 16\) vào biểu thức \(A\) rồi tính toán 

2. Qui đồng mẫu thức rồi thực hiện cộng trừ và rút gọn các phân thức.

3. Tìm \(A.B\) rồi cho \(AB = \dfrac{{\sqrt x  - 1}}{2}\) để giải phương trình ẩn \(x\) thu được.

Lời giải chi tiết:

Cho hai biểu thức \(A = \dfrac{{\sqrt x  + 1}}{{\sqrt x }}\) và \(B = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x  - 2}} + \dfrac{1}{{\sqrt x  + 2}}\) với \(x > 0;x \ne 4.\)

1. Tính giá trị của biểu thức \(A\) khi \(x = 16.\)

Thay \(x = 16\) (thỏa mãn điều kiện) vào biểu thức \(A\) ta được:

\(A = \dfrac{{\sqrt {16}  + 1}}{{\sqrt {16} }}\) \( = \dfrac{{4 + 1}}{4} = \dfrac{5}{4}.\)

Vậy với \(x = 16\) thì \(A = \dfrac{5}{4}.\)

2. Rút gọn biểu thức \(B.\)

Với \(x > 0;x \ne 4.\), ta có:

\(B = \dfrac{x}{{x - 4}} + \dfrac{1}{{\sqrt x  - 2}} + \dfrac{1}{{\sqrt x  + 2}}\)

\( = \dfrac{x}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}} + \dfrac{{\sqrt x  + 2}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\)\( + \dfrac{{\sqrt x  - 2}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\)

\(\begin{array}{l} = \dfrac{{x + \sqrt x  + 2 + \sqrt x  - 2}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\\ = \dfrac{{x + 2\sqrt x }}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\\ = \dfrac{{\sqrt x \left( {\sqrt x  + 2} \right)}}{{\left( {\sqrt x  - 2} \right)\left( {\sqrt x  + 2} \right)}}\\ = \dfrac{{\sqrt x }}{{\sqrt x  - 2}}\end{array}\)

 Với \(x > 0;x \ne 4.\) thì \(B = \dfrac{{\sqrt x }}{{\sqrt x  - 2}}\)

3. Tìm tất cả các giá trị của \(x\) để \(AB = \dfrac{{\sqrt x  - 1}}{2}.\)

Ta có: \(AB = \dfrac{{\sqrt x  + 1}}{{\sqrt x }}.\dfrac{{\sqrt x }}{{\sqrt x  - 2}}\) \( = \dfrac{{\sqrt x  + 1}}{{\sqrt x  - 2}}\)  với \(x > 0;x \ne 4.\)

Theo đề bài: \(AB = \dfrac{{\sqrt x  - 1}}{2}\)

\(\begin{array}{l} \Leftrightarrow \dfrac{{\sqrt x  + 1}}{{\sqrt x  - 2}} = \dfrac{{\sqrt x  - 1}}{2}\\ \Rightarrow 2\left( {\sqrt x  + 1} \right) = \left( {\sqrt x  - 2} \right)\left( {\sqrt x  - 1} \right)\\ \Leftrightarrow 2\sqrt x  + 2 = x - 3\sqrt x  + 2\\ \Leftrightarrow x - 5\sqrt x  = 0\\ \Leftrightarrow \sqrt x \left( {\sqrt x  - 5} \right) = 0\end{array}\)

\( \Leftrightarrow \sqrt x  - 5 = 0\) (do \(\sqrt x  > 0\)) 

\(\begin{array}{l} \Leftrightarrow \sqrt x  = 5\\ \Leftrightarrow x = 25\left( {tm} \right)\end{array}\)

Vậy với \(x = 25\) thì \(AB = \dfrac{{\sqrt x  - 1}}{2}\)

---

LG bài 2

Phương pháp giải:

1) Gọi số sản phẩm mỗi ngày phân xưởng sản xuất được theo kế hoạch là \(x\left( {x > 0} \right)\) sản phẩm

Lập phương trình theo \(x\), giải phương trình ta tìm được \(x\). 

Kết hợp điều kiện để kết luận.

2) Thể tích khối trụ bán kính đáy \(r\) và chiều cao \(h\) là \(V = \pi {r^2}h\)

Lời giải chi tiết:

1. Giải bài toán bằng cách lập hệ phương trình hoặc lập phương trình.

Một phân xưởng theo kế hoạch phải sản xuất 630 sản phẩm trong một số ngày quy định. Do mỗi ngày phân xưởng đó sản xuất vượt mức 5 sản phẩm nên phân xưởng hoàn thành kế hoạch sớm hơn thời gian quy định là 3 ngày. Hỏi theo kế hoạch, mỗi ngày phân xưởng phải sản xuất được bao nhiêu sản phẩm?

Gọi số sản phẩm mỗi ngày phân xưởng sản xuất được theo kế hoạch là \(x\left( {x > 0} \right)\) sản phẩm.

Thời gian phân xưởng hoàn thành theo kế hoạch là: \(\dfrac{{630}}{x}\) ngày

Theo thực tế, mỗi ngày phân  xưởng sản xuất được \(x + 5\) sản phẩm

Thời gian phân xưởng hoàn thành theo thực tế là: \(\dfrac{{630}}{{x + 5}}\) ngày

Vì phân xưởng hoàn thành kế hoạch sớm hơn thời gian quy định là 3 ngày, nên ta có phương trình:

\(\begin{array}{l}\dfrac{{630}}{x} - \dfrac{{630}}{{x + 5}} = 3\\ \Leftrightarrow \dfrac{{630\left( {x + 5} \right) - 630x}}{{x\left( {x + 5} \right)}} = 3\\ \Rightarrow 630x + 3150 - 630x = 3x\left( {x + 5} \right)\\ \Leftrightarrow 3{x^2} + 15x - 3150 = 0\\ \Leftrightarrow {x^2} + 5x - 1050 = 0\\ \Leftrightarrow {x^2} - 30x + 35x - 1050 = 0\\ \Leftrightarrow x\left( {x - 30} \right) + 35\left( {x - 30} \right) = 0\\ \Leftrightarrow \left( {x - 30} \right)\left( {x + 35} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 30 = 0\\x + 35 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 30\left( {tm} \right)\\x =  - 35\left( {ktm} \right)\end{array} \right.\end{array}\)

Vậy mỗi ngày phân xưởng sản xuất được theo kế hoạch là \(30\) sản phẩm.

2. Một lọ hoa hình trụ có đường kính đáy là 12cm, người ta đổ vào trong lọ một lượng nước với chiều cao của cột nước là 20cm. Tính thể tích nước trong lọ hoa.

Thể tích nước trong lọ hoa là thể tích hình trụ có bán kính đáy \(r = 12cm:2 = 6cm\) và chiều cao \(h = 20cm.\)

Thể tích nước là: \(V = \pi {r^2}h\) \( = \pi {.6^2}.20 = 720\pi \left( {c{m^3}} \right)\)

---

LG bài 3

Phương pháp giải:

1) Giải hệ phương trình bằng cách đặt ẩn phụ 

2) Phương trình \(a{x^2} + bx + c = 0\) có hai nghiệm \({x_1};{x_2}\) khi \(\left\{ \begin{array}{l}a \ne 0\\\Delta  \ge 0\end{array} \right.\)

Sử dụng hệ thức Vi-et: \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\)

Lời giải chi tiết:

1) Giải phương trình: \(\left\{ \begin{array}{l}\dfrac{1}{{x + 3}} - \dfrac{2}{{y - 1}} = 9\\\dfrac{3}{{x + 3}} + \dfrac{1}{{y - 1}} = 6\end{array} \right.\)

Điều kiện:  \(x \ne  - 3;y \ne 1\)

Đặt \(\left\{ \begin{array}{l}\dfrac{1}{{x + 3}} = u\\\dfrac{1}{{y - 1}} = v\end{array} \right.\) , ta có hệ phương trình:

\(\begin{array}{l}\left\{ \begin{array}{l}u - 2v = 9\\3u + v = 6\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}u - 2v = 9\\6u + 2v = 12\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}7u = 21\\u - 2v = 9\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}u = 3\\3 - 2v = 9\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}u = 3\\ - 2v = 6\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}u = 3\\v =  - 3\end{array} \right.\end{array}\)

Thay lại cách đặt ta được:

\(\begin{array}{l}\left\{ \begin{array}{l}\dfrac{1}{{x + 3}} = 3\\\dfrac{1}{{y - 1}} =  - 3\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x + 3 = \dfrac{1}{3}\\y - 1 =  - \dfrac{1}{3}\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x =  - \dfrac{8}{3}\left( {tm} \right)\\y = \dfrac{2}{3}\left( {tm} \right)\end{array} \right.\end{array}\)

Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( { - \dfrac{8}{3};\dfrac{2}{3}} \right)\)

2) Cho phương trình \({x^2} + mx + m - 1 = 0\) (1) với \(x\) là ẩn số và \(m\) là tham số.

a) Giải phương trình khi \(m = 2.\)

Thay \(m = 2\) vào phương trình (1) ta được:

\(\begin{array}{l}{x^2} + 2x + 1 = 0\\ \Leftrightarrow {\left( {x + 1} \right)^2} = 0\\ \Leftrightarrow x + 1 = 0\\ \Leftrightarrow x =  - 1\end{array}\)

Vậy với \(m = 2\) thì phương trình có nghiệm \(x =  - 1.\)

b) Tìm tất cả các giá trị của \(m\) để phương trình có hai nghiệm \({x_1};{x_2}\) sao cho \({x_1} = 2{x_2}\).

Phương trình (1) là phương trình bậc hai có: \(\Delta  = {m^2} - 4\left( {m - 1} \right)\) \( = {m^2} - 4m + 4\) \( = {\left( {m - 2} \right)^2}\)

Vì \({\left( {m - 2} \right)^2} \ge 0\) với mọi \(m\) nên \(\Delta  \ge 0\) với mọi \(m\)

Suy ra phương trình (1) luôn có hai nghiệm \({x_1};{x_2}\) với mọi \(m\)

Theo hệ thức Vi-et ta có:

\(\left\{ \begin{array}{l}{x_1} + {x_2} =  - m\left( * \right)\\{x_1}{x_2} = m - 1\end{array} \right.\)

Theo đề bài ta có: \({x_1} = 2{x_2}\)

Thay \({x_1} = 2{x_2}\) vào (*) ta được: \(2{x_2} + {x_2} = -m\) \( \Leftrightarrow 3{x_2} = -m \Leftrightarrow {x_2} = \dfrac{-m}{3}\)

\( \Rightarrow {x_1} = 2{x_2}\) \( = 2.\dfrac{-m}{3} = \dfrac{{-2m}}{3}\)

Thay \({x_1} = \dfrac{{-2m}}{3};{x_2} = \dfrac{-m}{3}\) vào phương trình \({x_1}{x_2} = m - 1\) ta được:

\(\begin{array}{l}\dfrac{{-2m}}{3}.\dfrac{-m}{3} = m - 1\\ \Leftrightarrow 2{m^2} = 9\left( {m - 1} \right)\\ \Leftrightarrow 2{m^2} - 9m + 9 = 0\\ \Leftrightarrow 2{m^2} - 6m - 3m + 9 = 0\\ \Leftrightarrow 2m\left( {m - 3} \right) - 3\left( {m - 3} \right) = 0\\ \Leftrightarrow \left( {2m - 3} \right)\left( {m - 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}2m - 3 = 0\\m - 3 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}m = \dfrac{3}{2}\\m = 3\end{array} \right.\end{array}\)

Vậy \(m = 3;m = \dfrac{3}{2}\) là các giá trị cần tìm. 

---

LG bài 4

Phương pháp giải:

1) Chứng minh tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp.

2) Chứng minh hai tam giác \(ABD\) và \(AEB\) đồng dạng, từ đó suy ra các cạnh tương ứng tỉ lệ.

3) Chứng minh \(AH.AO = A{B^2}\). 

Từ đó suy ra \(AH.AO = AD.AE\) và hai tam giác \(AHD\) và \(AEO\) đồng dạng.

Lời giải chi tiết:

Cho đường tròn \(\left( O \right)\) và một điểm A nằm ngoài đường tròn. Kẻ hai tiếp tuyến AB và AC với đường tròn (O), (B, C là tiếp điểm). Trên đoạn OB lấy điểm I (I khác B, I khác O). Đường thẳng AI cắt đường tròn (O) tại hai điểm D và E (D nằm giữa A và E)

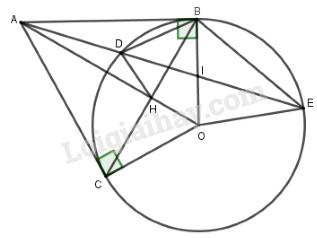
1. Chứng minh rằng tứ giác ABOC nội tiếp 

Ta có:

AB là tiếp tuyến với đường tròn nên \(AB \bot OB \Rightarrow \widehat {ABO} = {90^0}\) (tính chất)

AC là tiếp tuyến với đường tròn nên \(AC \bot OC \Rightarrow \widehat {ACO} = {90^0}\) (tính chất)

Tứ giác ABOC có:

\(\widehat {ABO} + \widehat {ACO}\) \( = {90^0} + {90^0} = {180^0}\)

Do đó ABOC là tứ giác nội tiếp (tứ giác có tổng hai góc đối bằng \({180^0}\) là tứ giác nội tiếp)

Vậy tứ giác ABOC nội tiếp (đpcm).

2. Chứng minh \(A{B^2} = AD.AE\)

Xét tam giác \(ABD\) và \(AEB\) có:

\(\widehat {ABD} = \widehat {AEB}\) (góc giữa tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(BD\))

\(\widehat A\) chung

\( \Rightarrow \Delta ABD \backsim \Delta AEB\left( {g - g} \right)\)

\( \Rightarrow \dfrac{{AB}}{{AE}} = \dfrac{{AD}}{{AB}}\) (cạnh tương ứng)

\( \Rightarrow A{B^2} = AE.AD\) (đpcm)

3. Gọi H là giao điểm của \(BC\) và \(AO.\) Chứng minh rằng \(\widehat {AHD} = \widehat {AEO}\).

Ta có: AB=AC; OB=OC nên AO là đường trung trực của BC.

Do đó AO vuông góc với BC tại trung điểm H của BC.

\( \Rightarrow AO \bot BC\) tại H.

Xét tam giác \(ABO\) vuông tại B có BH là đường cao nên \(AH.AO = A{B^2}\) (hệ thức giữa cạnh và đường cao trong tam giác vuông)

Lại có: \(A{B^2} = AD.AE\left( {cmt} \right)\)

Do đó \(AH.AO = AD.AE\) \( \Rightarrow \dfrac{{AH}}{{AE}} = \dfrac{{AD}}{{AO}}\)

Xét \(\Delta AHD\) và \(\Delta AEO\) có:

\(\widehat A\) chung

\(\dfrac{{AH}}{{AE}} = \dfrac{{AD}}{{AO}}\)(cmt)

\( \Rightarrow \Delta AHD \backsim \Delta AEO\left( {g - g} \right)\)

\( \Rightarrow \widehat {AHD} = \widehat {AEO}\) (góc tương ứng) (đpcm)

---

LG bài 5

Phương pháp giải:

Đánh giá \(VT \le 2\) bằng cách áp dung BĐT Bunhia \({\left( {ax + by} \right)^2} \le \left( {{a^2} + {b^2}} \right)\left( {{x^2} + {y^2}} \right)\).

Đánh giá \(VP \ge 2\) bằng cách đưa về dạng \(a{\left( {x + {x_0}} \right)^2} + b\).

Từ đó suy ra nghiệm của phương trình đã cho.

Lời giải chi tiết:

Giải phương trình \(\sqrt {x - 2}  + \sqrt {4 - x}  = {x^2} - 6x + 11\)

ĐK: \(\left\{ \begin{array}{l}x - 2 \ge 0\\4 - x \le 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 2\\x \le 4\end{array} \right.\) \( \Leftrightarrow 2 \le x \le 4\)

Áp dụng BĐT Bunhia ta có:

\(\begin{array}{l}V{T^2} = {\left( {\sqrt {x - 2}  + \sqrt {4 - x} } \right)^2}\\ = {\left( {1.\sqrt {x - 2}  + 1.\sqrt {4 - x} } \right)^2}\\ \le \left[ {{1^2} + {1^2}} \right]\left[ {{{\left( {\sqrt {x - 2} } \right)}^2} + {{\left( {\sqrt {4 - x} } \right)}^2}} \right]\\ = \left( {1 + 1} \right)\left( {x - 2 + 4 - x} \right)\\ = 2.2 = 4\\ \Rightarrow V{T^2} \le 4\\ \Rightarrow VT \le 2\end{array}\)

Lại có,

\(\begin{array}{l}VP = {x^2} - 6x + 11\\ = {x^2} - 6x + 9 + 2\\ = {\left( {x - 3} \right)^2} + 2 \ge 2\\\left( {do\,{{\left( {x - 3} \right)}^2} \ge 0,\forall x} \right)\\ \Rightarrow VP \ge 2\end{array}\)

Do đó \(VT \le 2 \le VP\).

Dấu “=” xảy ra khi \(VT = 2 = VP\)

\( \Leftrightarrow {\left( {x - 3} \right)^2} = 0 \Leftrightarrow x = 3\left( {TMĐK} \right)\).

Vậy phương trình có nghiệm duy nhất \(x = 3\).

HẾT