Giải đề thi học kì 2 toán lớp 9 năm 2019 - 2020 PGD quận Ba Đình

Đề bài

Bài 1  (2,0 điểm): Cho hai biểu thức:

\(A = \dfrac{{\sqrt x }}{{\sqrt x  - 3}} + \dfrac{3}{{\sqrt x  + 2}} + \dfrac{{5\sqrt x }}{{\left( {\sqrt x  + 2} \right)\left( {3 - \sqrt x } \right)}}\)  và  \(B = \dfrac{{\sqrt x  + 5}}{{\sqrt x  + 2}}\)  với \(x \ge 0;x \ne 9\).

1. Tính giá trị của \(B\) khi \(x = 4.\)

2. Rút gọn biểu thức \(A\)

3. Cho \(S = A:B\), so sánh \(S\) với \(\dfrac{3}{5}\).

Bài 2 (2,5 điểm):

1. Giải bài toán bằng cách lập phương trình hoặc hệ phương trình

Một công nhân phải may 120 chiếc khẩu trang vải trong 1 thời gian quy định. Khi thực hiện, nhờ cải tiến kỹ thuật nên mỗi giờ người đó may thêm được 3 chiếc khẩu trang và hoàn thành kế hoạch sớm hơn 2 giờ. Tính số khẩu trang công nhân phải may trong 1 giờ theo quy định?

2. Người ta làm các viên đá hình cầu có bán kính là 2cm. Cho 6 viên đá như vậy vào một cốc thủy tinh hình trụ rồi rót nước giải khát vào cho đầy cốc. Biết rằng cột nước hình trụ ở cốc có bán kính đáy là 3cm và chiều cao cột nước là 12cm. Tính thể tích nước giải khát rót vào cốc? (Lấy \(\pi  \approx 3,14\), kết quả làm tròn đến chữ số thập phân thứ hai).

Bài 3 (2,0 điểm):

1. Giải hệ phương trình \(\left\{ \begin{array}{l}\sqrt {x - 1}  - 2y = 9\\3\sqrt {x - 1}  + y = 6\end{array} \right.\) .

2. Cho phương trình \({x^2} - \left( {m + 2} \right)x + m = 0\)

a) Chứng minh phương trình luôn có 2 nghiệm phân biệt với mọi \(m.\)

b) Tìm \(m\) để phương trình có 2 nghiệm phân biệt \({x_1};{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 7\)

Bài 4 (3 điểm):

Từ điểm M nằm ngoài đường tròn tâm O, vẽ các tiếp tuyến MA và MB với đường tròn \(\left( O \right),A\) và \(B\) là hai tiếp điểm; vẽ cát tuyến MCD đến đường tròn (O) sao cho tia MC nằm giữa hai tia MA và MO (biết điểm C nằm giữa hai điểm M và D).

1. Chứng minh: tứ giác MAOB nội tiếp được

2. Chứng minh: \(M{A^2} = MC.MD\)

3. Vẽ dây BI của đường tròn (O) sao cho BI song song với MD, AI cắt CD tại H, kéo dài AB cắt OH tại K. Chứng minh H là trung điểm của CD và KD là tiếp tuyến của đường tròn (O).

Bài 5 (0,5 điểm): 

Giải phương trình: \(\sqrt {2x - 5}  + 2\sqrt {7 - x} \) \( = \sqrt 3 {x^2} - 8\sqrt 3 x + 19\sqrt 3 \)

HẾT

---

LG bài 1

Phương pháp giải:

1) Thay \(x = 4\) vào biểu thức \(B\) rồi tính toán

2) Qui đồng mẫu các phân thức rồi rút gọn với mẫu thức chung là \(\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 3} \right)\)

3) Rút gọn \(S = A:B\) sau đó so sánh hiệu \(P - \dfrac{3}{5}\) với số \(0.\)

Lời giải chi tiết:

Cho hai biểu thức:

\(A = \dfrac{{\sqrt x }}{{\sqrt x  - 3}} + \dfrac{3}{{\sqrt x  + 2}} + \dfrac{{5\sqrt x }}{{\left( {\sqrt x  + 2} \right)\left( {3 - \sqrt x } \right)}}\)  và  \(B = \dfrac{{\sqrt x  + 5}}{{\sqrt x  + 2}}\)  với \(x \ge 0;x \ne 9\).

1. Tính giá trị của \(B\) khi \(x = 4.\)

Thay \(x = 4\) (thỏa mãn điều kiện) vào biểu thức \(B\) ta được:

\(B = \dfrac{{\sqrt 4  + 5}}{{\sqrt 4  + 2}}\) \( = \dfrac{{2 + 5}}{{2 + 2}} = \dfrac{7}{4}\)

Vậy với \(x = 4\) thì \(B = \dfrac{7}{4}\).

2. Rút gọn biểu thức \(A\)

Với \(x \ge 0;x \ne 9\) ta có:

\(A = \dfrac{{\sqrt x }}{{\sqrt x  - 3}} + \dfrac{3}{{\sqrt x  + 2}} + \dfrac{{5\sqrt x }}{{\left( {\sqrt x  + 2} \right)\left( {3 - \sqrt x } \right)}}\)

\( = \dfrac{{\sqrt x }}{{\sqrt x  - 3}} + \dfrac{3}{{\sqrt x  + 2}} - \dfrac{{5\sqrt x }}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 3} \right)}}\)

\( = \dfrac{{\sqrt x \left( {\sqrt x  + 2} \right)}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 3} \right)}} + \dfrac{{3\left( {\sqrt x  - 3} \right)}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 3} \right)}}\) \( - \dfrac{{5\sqrt x }}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 3} \right)}}\)

\(\begin{array}{l} = \dfrac{{\sqrt x \left( {\sqrt x  + 2} \right) + 3\left( {\sqrt x  - 3} \right) - 5\sqrt x }}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 3} \right)}}\\ = \dfrac{{x + 2\sqrt x  + 3\sqrt x  - 9 - 5\sqrt x }}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 3} \right)}}\\ = \dfrac{{x - 9}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 3} \right)}}\\ = \dfrac{{\left( {\sqrt x  + 3} \right)\left( {\sqrt x  - 3} \right)}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 3} \right)}}\\ = \dfrac{{\sqrt x  + 3}}{{\sqrt x  + 2}}\end{array}\)

Vậy \(A = \dfrac{{\sqrt x  + 3}}{{\sqrt x  + 2}}\) với \(x \ge 0;x \ne 9.\)

3. Cho \(S = A:B\), so sánh \(S\) với \(\dfrac{3}{5}\).

Với \(x \ge 0;x \ne 9\) ta có:

\(S = A:B\) \( = \dfrac{{\sqrt x  + 3}}{{\sqrt x  + 2}}:\dfrac{{\sqrt x  + 5}}{{\sqrt x  + 2}}\) \( = \dfrac{{\sqrt x  + 3}}{{\sqrt x  + 2}}.\dfrac{{\sqrt x  + 2}}{{\sqrt x  + 5}}\) \( = \dfrac{{\sqrt x  + 3}}{{\sqrt x  + 5}}\)

Xét hiệu \(S - \dfrac{3}{5} = \dfrac{{\sqrt x  + 3}}{{\sqrt x  + 5}} - \dfrac{3}{5}\)

\(\begin{array}{l} = \dfrac{{5\left( {\sqrt x  + 3} \right) - 3\left( {\sqrt x  + 5} \right)}}{{5\left( {\sqrt x  + 5} \right)}}\\ = \dfrac{{5\sqrt x  + 15 - 3\sqrt x  - 15}}{{5\left( {\sqrt x  + 5} \right)}}\\ = \dfrac{{2\sqrt x }}{{5\left( {\sqrt x  + 5} \right)}}\end{array}\) 

Với \(x \ge 0,x \ne 9\) ta có \(2\sqrt x  \ge 0\) và \(5\left( {\sqrt x  + 5} \right) > 0\) nên \(\dfrac{{2\sqrt x }}{{5\left( {\sqrt x  + 5} \right)}} \ge 0\)

Hay \(S - \dfrac{3}{5} \ge 0 \Leftrightarrow S \ge \dfrac{3}{5}.\)

Vậy \(S \ge \dfrac{3}{5}\) với \(x \ge 0;x \ne 9.\)

---

LG bài 2

Phương pháp giải:

1) Gọi số khẩu trang công nhân phải may trong 1 giờ theo quy định là \(x\left( {x > 0} \right)\)

Lập phương trình theo ẩn \(x\) rồi giải phương trình thu được. 

2) Thể tích khối cầu bán kính \(R\) là \(V = \dfrac{4}{3}\pi {R^3}\)

Thể tích khối trụ có bán kính đáy \(r\) và chiều cao \(h\) là \(v = \pi {r^2}h\)

Lời giải chi tiết:

1. Giải bài toán bằng cách lập phương trình hoặc hệ phương trình

Một công nhân phải may 120 chiếc khẩu trang vải trong 1 thời gian quy định. Khi thực hiện, nhờ cải tiến kỹ thuật nên mỗi giờ người đó may thêm được 3 chiếc khẩu trang và hoàn thành kế hoạch sớm hơn 2 giờ. Tính số khẩu trang công nhân phải may trong 1 giờ theo quy định?

Gọi số khẩu trang công nhân phải may trong 1 giờ theo quy định là \(x\left( {x > 0} \right)\)(chiếc)

Thời gian công nhân may 120 chiếc khẩu trang theo quy định là \(\dfrac{{120}}{x}\) giờ

Theo thực tế, mỗi giờ công nhân may được số khẩu trang là \(x + 3\) chiếc

Thời gian công nhân may 120 chiếc khẩu trang theo thực tế là \(\dfrac{{120}}{{x + 3}}\) giờ

Vì công nhân hoành thành kế hoạch sớm hơn 2 giờ nên ta có phương trình:

\(\dfrac{{120}}{x} - \dfrac{{120}}{{x + 3}} = 2\)

\(\begin{array}{l} \Leftrightarrow \dfrac{{120\left( {x + 3} \right) - 120x}}{{x\left( {x + 3} \right)}} = 2\\ \Leftrightarrow \dfrac{{120x + 360 - 120x}}{{x\left( {x + 3} \right)}} = 2\\ \Leftrightarrow \dfrac{{360}}{{{x^2} + 3x}} = 2\\ \Rightarrow 360 = 2{x^2} + 6x\\ \Leftrightarrow 2{x^2} + 6x - 360 = 0\\ \Leftrightarrow {x^2} + 3x - 180 = 0\\ \Leftrightarrow {x^2} - 12x + 15x - 180 = 0\\ \Leftrightarrow x\left( {x - 12} \right) + 15\left( {x - 12} \right) = 0\\ \Leftrightarrow \left( {x - 12} \right)\left( {x + 15} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}x - 12 = 0\\x + 15 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 12\left( {tm} \right)\\x =  - 15\left( {ktm} \right)\end{array} \right.\end{array}\)

Vậy số khẩu trang công nhân phải may trong 1 giờ theo quy định là \(12\) chiếc.

2. Người ta làm các viên đá hình cầu có bán kính là 2cm. Cho 6 viên đá như vậy vào một cốc thủy tinh hình trụ rồi rót nước giải khát vào cho đầy cốc. Biết rằng cột nước hình trụ ở cốc có bán kính đáy là 3cm và chiều cao cột nước là 12cm. Tính thể tích nước giải khát rót vào cốc? (Lấy \(\pi  \approx 3,14\), kết quả làm tròn đến chữ số thập phân thứ hai).

Thể tích cốc nước hình trụ có bán kính đáy \(3cm\) và chiều cao \(12cm\) là \({V_1} = \pi {.3^2}.12 = 108\pi \left( {c{m^3}} \right)\) 

Thể tích 6 viên đá hình cầu bán kính 2cm là \({V_2} = 6.\dfrac{4}{3}\pi {.2^3} = 64\pi \left( {c{m^3}} \right)\)

Thể tích nước giải khát rót vào cốc là \(V = {V_1} - {V_2}\)\( = 108\pi  - 64\pi \) \( = 44\pi  \approx 138,16\left( {c{m^3}} \right)\)

---

LG bài 3

Phương pháp giải:

1) Giải hệ phương trình bằng cách đặt ẩn phụ và dùng phương pháp cộng đại số

2) a) Phương trình có hai nghiệm phân biệt khi \(\left\{ \begin{array}{l}a \ne 0\\\Delta  > 0\end{array} \right.\)

b) Sử dụng hệ thức Vi-et: \(\left\{ \begin{array}{l}{x_1} + {x_2} =  - \dfrac{b}{a}\\{x_1}{x_2} = \dfrac{c}{a}\end{array} \right.\)

Lời giải chi tiết:

1. Giải hệ phương trình \(\left\{ \begin{array}{l}\sqrt {x - 1}  - 2y = 9\\3\sqrt {x - 1}  + y = 6\end{array} \right.\)

Điều kiện: \(x \ge 1\)

Đặt \(\sqrt {x - 1}  = u\left( {u \ge 0} \right)\), ta có hệ phương trình:

\(\begin{array}{l}\left\{ \begin{array}{l}u - 2y = 9\\3u + y = 6\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}u - 2y = 9\\6u + 2y = 12\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}u - 2y = 9\\7u = 21\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}u = 3\\3 - 2y = 9\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}u = 3\\ - 2y = 6\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}u = 3\left( {tm} \right)\\y =  - 3\end{array} \right.\end{array}\)

Với \(u = 3\) ta có \(\sqrt {x - 1}  = 3\) \( \Leftrightarrow x - 1 = 9\)\( \Leftrightarrow x = 10\) (thỏa mãn)

Vậy hệ phương trình có nghiệm \(\left( {x;y} \right) = \left( {10; - 3} \right)\)

2. Cho phương trình \({x^2} - \left( {m + 2} \right)x + m = 0\)

a) Chứng minh phương trình luôn có 2 nghiệm phân biệt với mọi \(m.\)

Phương trình \({x^2} - \left( {m + 2} \right)x + m = 0\) là phương trình bậc hai có:

\(\Delta  = {\left( {m + 2} \right)^2} - 4m\) \( = {m^2} + 4m + 4 - 4m\) \( = {m^2} + 4\)

Vì \({m^2} \ge 0\) với mọi \(m\) nên \({m^2} + 4 \ge 4 > 0\) với mọi \(m\).

Suy ra phương trình \({x^2} - \left( {m + 2} \right)x + m = 0\) luôn có 2 nghiệm phân biệt với mọi \(m.\)

b) Tìm \(m\) để phương trình có 2 nghiệm phân biệt \({x_1};{x_2}\) thỏa mãn \(x_1^2 + x_2^2 = 7\)

Từ câu a) ta có phương trình \({x^2} - \left( {m + 2} \right)x + m = 0\) luôn có 2 nghiệm phân biệt \({x_1};{x_2}\) với mọi \(m.\)

Theo hệ thức Vi-et ta có:

\(\left\{ \begin{array}{l}{x_1} + {x_2} = m + 2\\{x_1}.{x_2} = m\end{array} \right.\)

Ta có: \(x_1^2 + x_2^2 = 7\)

\(\begin{array}{l} \Leftrightarrow {\left( {{x_1} + {x_2}} \right)^2} - 2{x_2}{x_2} = 7\\ \Leftrightarrow {\left( {m + 2} \right)^2} - 2m = 7\\ \Leftrightarrow {m^2} + 4m + 4 - 2m - 7 = 0\\ \Leftrightarrow {m^2} + 2m - 3 = 0\\ \Leftrightarrow {m^2} - m + 3m - 3 = 0\\ \Leftrightarrow m\left( {m - 1} \right) + 3\left( {m - 1} \right) = 0\\ \Leftrightarrow \left( {m - 1} \right)\left( {m + 3} \right) = 0\\ \Leftrightarrow \left[ \begin{array}{l}m - 1 = 0\\m + 3 = 0\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}m = 1\\m =  - 3\end{array} \right.\end{array}\)

Vậy \(m = 1;m =  - 3\) thỏa mãn yêu cầu đề bài.

---

LG bài 4

Phương pháp giải:

1) Chứng minh bốn điểm M, A, O, B cùng thuộc đường tròn đường kính OM.

2) Chứng minh hai tam giác MCA và MAD đồng dạng theo trường hợp góc – góc.

3) +) Chứng minh bốn điểm M, A, H, B cùng thuộc một đường tròn.

Từ đó suy ra H thuộc đường tròn đường kính OM và \(\widehat {OHM} = {90^0}\).

+) Chứng minh hai tam giác OHM và OFK đồng dạng với F là giao điểm của OM và AB.

Chứng minh OH.OK=OF.OM=\(O{D^2}\)

Từ đó suy ra hai tam giác OHD và ODK đồng dạng.

Lời giải chi tiết:

Từ điểm M nằm ngoài đường tròn tâm O, vẽ các tiếp tuyến MA và MB với đường tròn \(\left( O \right),A\) và \(B\) là hai tiếp điểm; vẽ cát tuyến MCD đến đường tròn (O) sao cho tia MC nằm giữa hai tia MA và MO (biết điểm C nằm giữa hai điểm M và D).

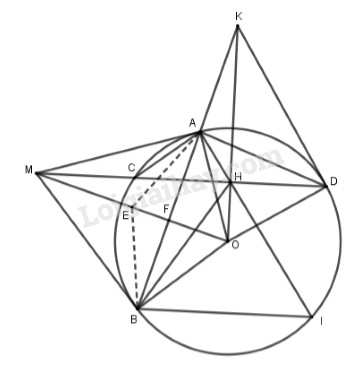
1. Chứng minh: tứ giác MAOB nội tiếp được

Ta có:

MA là tiếp tuyến với đường tròn nên \(MA \bot OA \Rightarrow \widehat {MAO} = {90^0}\) (tính chất)

MB là tiếp tuyến với đường tròn nên \(MB \bot OB \Rightarrow \widehat {MBO} = {90^0}\) (tính chất)

Gọi E là trung điểm của OM thì:

\(AE = EM = EO = \dfrac{1}{2}OM\) (do tam giác MAO vuông tại A)

\(BE = EM = EO = \dfrac{1}{2}OM\) (do tam giác MBO vuông tại B)

Do đó \(EA = EM = EO = EB\) hay 4 điểm \(A,M,O,B\) cùng thuộc đường tròn đường kính OM

Vậy tứ giác MAOB nội tiếp (đpcm).

2. Chứng minh: \(M{A^2} = MC.MD\)

Xét tam giác \(MAC\) và \(MDA\) có:

\(\widehat {MAC} = \widehat {MDA}\) (góc giữa tiếp tuyến và dây cung và góc nội tiếp cùng chắn cung \(AC\))

\(\widehat M\) chung

\( \Rightarrow \Delta MAC \backsim \Delta MDA\left( {g - g} \right)\)

\( \Rightarrow \dfrac{{MA}}{{MD}} = \dfrac{{MC}}{{MA}}\) (cạnh tương ứng)

\( \Rightarrow M{A^2} = MC.MD\) (đpcm)

3. Vẽ dây BI của đường tròn (O) sao cho BI song song với MD, AI cắt CD tại H, kéo dài AB cắt OH tại K. Chứng minh H là trung điểm của CD và KD là tiếp tuyến của đường tròn (O).

Ta có: \(BI//CD\) nên \(\widehat {AHC} = \widehat {AIB}\) (đồng vị)

Mà \(\widehat {AIB} = \widehat {ABM}\) (góc nội tiếp và góc tạo bởi tiếp tuyến và dây cung cùng chắn cung AB)

Nên \(\widehat {AHC} = \widehat {AHM} = \widehat {ABM}\) \(\left( { = \widehat {AIB}} \right)\)

Do đó tứ giác AHBM nội tiếp (hai đỉnh kề một cạnh nhìn cạnh đối diện các góc bằng nhau)

\( \Rightarrow A,H,B,M\) cùng thuộc một đường tròn.

Mà \(A,O,B,M\) cùng thuộc đường tròn đường kính OM (cmt) nên H cùng nằm trên đường tròn đường kính OM.

Do đó \(\widehat {MHO} = {90^0}\) hay \(OH \bot CD\)

\( \Rightarrow H\) là trung điểm của CD (đường kính vuông góc với dây cung thì đi qua trung điểm của dây ấy) (đpcm).

Gọi F là giao điểm của OM và AB.

Khi đó \(\widehat {OFA} = \widehat {OFK} = {90^0}\).

Xét \(\Delta OFK\) và \(\Delta OHM\) có:

\(\widehat {OFK} = \widehat {OHM} = {90^0}\)

Chung \(\widehat O\)

\( \Rightarrow \Delta OFK \backsim \Delta OHM\left( {g - g} \right)\)

\( \Rightarrow \dfrac{{OF}}{{OH}} = \dfrac{{OK}}{{OM}}\) (cạnh tương ứng)

\( \Rightarrow OF.OM = OH.OK\) (1)

Tam giác OAM vuông tại A có AF là đường cao nên:

\(OF.OM = O{A^2}\) (hệ thức giữa cạnh và đường cao trong tam giác vuông) (2)

Từ (1) và (2) suy ra \(OF.OM = OH.OK = O{A^2} = O{D^2}\)

\(\begin{array}{l} \Rightarrow OH.OK = O{D^2}\\ \Rightarrow \dfrac{{OH}}{{OD}} = \dfrac{{OD}}{{OK}}\end{array}\)

Xét \(\Delta OHD\) và \(\Delta ODK\) có:

Chung \(\widehat O\)

\(\dfrac{{OH}}{{OD}} = \dfrac{{OD}}{{OK}}\,\,\left( {cmt} \right)\)

\( \Rightarrow \Delta OHD \backsim \Delta ODK\left( {c - g - c} \right)\)

\( \Rightarrow \widehat {OHD} = \widehat {ODK} = {90^0}\) (góc tương ứng)

Mà \(\widehat {OHD} = {90^0}\) nên \(\widehat {ODK} = {90^0} \Rightarrow OD \bot OK\)

Vậy KD là tiếp tuyến với đường tròn tại D (đpcm).

---

LG bài 5

Phương pháp giải:

Đánh giá \(VT \le 3\sqrt 3 \) bằng cách áp dụng BĐT Bunhia \({\left( {ax + by} \right)^2} \le \left( {{a^2} + {b^2}} \right)\left( {{x^2} + {y^2}} \right)\).

Đánh giá \(VP \ge 3\sqrt 3 \) bằng cách đưa về dạng \(a{\left( {x + {x_0}} \right)^2} + b\).

Từ đó suy ra nghiệm của phương trình đã cho.

Lời giải chi tiết:

Giải phương trình: \(\sqrt {2x - 5}  + 2\sqrt {7 - x} \) \( = \sqrt 3 {x^2} - 8\sqrt 3 x + 19\sqrt 3 \)

ĐK: \(\left\{ \begin{array}{l}2x - 5 \ge 0\\7 - x \ge 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge \dfrac{5}{2}\\x \le 7\end{array} \right.\) \( \Leftrightarrow \dfrac{5}{2} \le x \le 7\) 

Áp dụng BĐT Bunhia ta có:

\(\begin{array}{l}V{T^2} = {\left( {\sqrt {2x - 5}  + 2\sqrt {7 - x} } \right)^2}\\ = {\left( {1.\sqrt {2x - 5}  + \sqrt 2 .\sqrt {14 - 2x} } \right)^2}\\ \le \left[ {{1^2} + {{\left( {\sqrt 2 } \right)}^2}} \right]\left[ {{{\left( {\sqrt {2x - 5} } \right)}^2} + {{\left( {\sqrt {14 - 2x} } \right)}^2}} \right]\\ = \left( {1 + 2} \right)\left( {2x - 5 + 14 - 2x} \right)\\ = 3.9 = 27\\ \Rightarrow V{T^2} \le 27\\ \Rightarrow VT \le 3\sqrt 3 \end{array}\)

Lại có,

\(\begin{array}{l}VP = \sqrt 3 {x^2} - 8\sqrt 3 x + 19\sqrt 3 \\ = \sqrt 3 \left( {{x^2} - 8x + 16} \right) + 3\sqrt 3 \\ = \sqrt 3 {\left( {x - 4} \right)^2} + 3\sqrt 3 \\ \ge \sqrt 3 .0 + 3\sqrt 3 \\ = 3\sqrt 3 \\ \Rightarrow VP \ge \sqrt 3 \end{array}\)

Do đó \(VT \le 3\sqrt 3  \le VP\).

Dấu “=” xảy ra khi \(VT = 3\sqrt 3  = VP\)

\( \Leftrightarrow {\left( {x - 4} \right)^2} = 0 \Leftrightarrow x = 4\).

HẾT