Giải đề thi học kì 2 toán lớp 7 năm 2020 - 2021 trường Archimedes

Đề bài

Bài 1. (2,0 điểm)

Cho đơn thức \(A = \left( {\frac{2}{3}{x^3}y} \right).{\left( {\frac{1}{2}x{y^2}} \right)^3}.\left( {\frac{{ - 8}}{5}{x^2}} \right)\)

a) Thu gọn, xác định hệ số, phần biến và bậc của đơn thức A;

b) Tính giá trị của biểu thức A tại \(x = 2;\,\,y = \frac{{ - 1}}{2}\).

Bài 2. (2,0 điểm) Cho hai đa thức

\(P(x) = {x^4} + 3{x^3} - x + \frac{1}{2} - {x^3} - 4x\)

\(Q(x) = \frac{3}{2} - 4{x^3} + {x^4} - 2x - 3x + 2{x^3}.\)

a) Thu gọn và sắp xếp các đa thức P(x), Q(x) theo lũy thừa giảm của biến.

b) Tính \(P(x) + Q(x);\,\,P(x) - Q(x)\).

Bài 3. (2,0 điểm) Tìm nghiệm của các đa thức sau:

a) \(A(x) = 3x - 2;\)

b) \(B(x) = 2(3x - 1) - 5(x - 1);\)

c) \(C(x) = \frac{1}{2}{x^3} - 2x;\)

d) \(D(x) = 2{x^2} - 5x - 7\).

Bài 4. (3,5 điểm) Cho tam giác ABC cân tại A và \(\widehat A < {90^0}\), CD là tia phân giác của góc ACB (D\( \in \)AB). Từ D kẻ DE \( \bot \) AC tại E, DF \( \bot \) BC tại F. Đường thẳng DE cắt BC tại K, đường thẳng DF cắt AC tại H.

a) Chứng minh \(\Delta \)ECD = \(\Delta \)FCD;

b) Chứng minh \(\Delta \)ECK = \(\Delta \)FCH;

c) Gọi M là trung điểm của HK. Chứng minh ba điểm C, D, M thẳng hàng.

Bài 5. (0,5 điểm) Cho đa thức \(f\left( x \right){\rm{ }} = {\rm{ }}a{x^2} + bx + c\) với a, b, c là các hằng số.

Biết \(f\left( 0 \right),f\left( 1 \right),f\left( { - 1} \right),f\left( {\frac{{ - 1}}{2}} \right)\) là các số nguyên. Chứng minh rằng a, b, c là các số nguyên.

LG bài 1

Phương pháp giải:

a) Rút gọn A

b) Thay \(x = 2;\,\,y = \frac{{ - 1}}{2}\) vào A

Lời giải chi tiết:

a)

\(\begin{array}{l}A = \left( {\frac{2}{3}{x^3}y} \right).{\left( {\frac{1}{2}x{y^2}} \right)^3}.\left( {\frac{{ - 8}}{5}{x^2}} \right)\\A = \left( {\frac{2}{3}.\frac{1}{2}.\frac{{ - 8}}{5}} \right).\left( {{x^3}.{x^3}.{x^2}} \right).\left( {y.{y^6}} \right)\\A = \frac{{ - 8}}{{15}}.{x^8}.{y^7}\end{array}\)

b)

Thay \(x = 2;\,\,y = \frac{{ - 1}}{2}\) vào A ta được:

\(\begin{array}{l}A = \frac{{ - 8}}{{15}}{.2^8}.{\left( {\frac{{ - 1}}{2}} \right)^7}\\A = \frac{{16}}{{15}}\end{array}\)

LG bài 2

Phương pháp giải:

a) Thu gọn và sắp xếp.

b) Đặt tính rồi tính

Lời giải chi tiết:

a)

\(\begin{array}{l}P(x) = {x^4} + 3{x^3} - x + \frac{1}{2} - {x^3} - 4x\\P(x) = {x^4} + (3{x^3} - {x^3}) - (x + 4x) + \frac{1}{2}\\P(x) = {x^4} + 2{x^3} - 5x + \frac{1}{2}\end{array}\)

\(\begin{array}{l}Q(x) = \frac{3}{2} - 4{x^3} + {x^4} - 2x - 3x + 2{x^3}.\\Q(x) = {x^4} + ( - 4{x^3} + 2{x^3}) - (2x + 3x) + \frac{3}{2}\\Q(x) = {x^4} - 2{x^3} - 5x + \frac{3}{2}\end{array}\)

b)

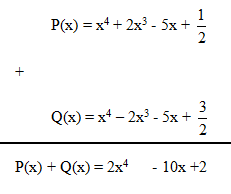
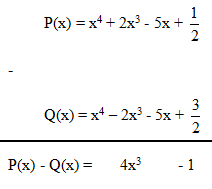
LG bài 3

Phương pháp giải:

Cho các đa thức bằng 0 rồi giải tìm x

Lời giải chi tiết:

a)

\(\begin{array}{l}A(x) = 0 \Leftrightarrow 3x - 2 = 0\\ \Leftrightarrow 3x = 2 \Leftrightarrow x = \frac{2}{3}\end{array}\)

Vậy nghiệm của đã thức A(x) là \(x = \frac{2}{3}\)

b)

\(\begin{array}{l}B(x) = 0\\ \Leftrightarrow 2(3x - 1) - 5(x - 1) = 0\\ \Leftrightarrow 6x - 2 - 5x + 5 = 0\\ \Leftrightarrow x + 3 = 0\\ \Leftrightarrow x =  - 3\end{array}\)

Vậy nghiệm của đã thức B(x) là \(x =  - 3\).

c)

\(\begin{array}{l}C(x) = 0\\ \Leftrightarrow \frac{1}{2}{x^3} - 2x = 0\\ \Leftrightarrow \frac{1}{2}x\left( {{x^2} - 4} \right) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{\frac{1}{2}x = 0}\\{{x^2} - 4 = 0}\end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x = 0}\\{x =  \pm 2}\end{array}} \right.\end{array}\)

Vậy tập  nghiệm của đa thức C(x) là \(\{ 0;\,2: - 2\} \)

d)

\(\begin{array}{l}D(x) = 0\\ \Leftrightarrow 2{x^2} - 5x - 7 = 0\\ \Leftrightarrow 2{x^2} + 2x - 7x - 7 = 0\\ \Leftrightarrow 2x(x + 1) - 7(x + 1) = 0\\ \Leftrightarrow (x + 1)(2x - 7) = 0\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x + 1 = 0}\\{2x - 7 = 0}\end{array}} \right.\\ \Leftrightarrow \left[ {\begin{array}{*{20}{c}}{x =  - 1}\\{x = \frac{7}{2}}\end{array}} \right.\end{array}\).

Vậy nghiệm của đa thức D(x) là -1 và \(\frac{7}{2}\)

LG bài 4

Phương pháp giải:

a) Hai tam giác bằng nhau theo trường hợp cạnh huyền - góc nhọn

b)  Hai tam giác bằng nhau theo trường hợp góc - cạnh - góc

c) Sử dụng tính chất 3 đường cao trong 1 tam giác đồng quy

Lời giải chi tiết:

a)

Xét \(\Delta ECD\) và \(\Delta FCD\) có:

\(\widehat {CFD} = \widehat {CED} = {90^0}\)

\(\widehat {{C_1}} = \widehat {{C_2}}\) (do CD là phân giác góc C)

CD chung

=> \(\Delta ECD\) = \(\Delta FCD\) (ch.gn) (1)

b)

Do (1) nên EC = FC

Xét \(\Delta ECK\) và \(\Delta FCH\) có:

\(\widehat {KEC} = \widehat {HFC} = {90^0}\)

EC = FC

\(\widehat C\) chung

=> \(\Delta ECK\) = \(\Delta FCH\) (g.c.g) (2)

c)

Ta có:

\(KE \bot HC\) và \(HF \bot KC\)

\(HF \cap KE = \left\{ D \right\}\)

=> D là trực tâm tam giác HKC

=> \(CD \bot HK\)(3)

Do (2) suy ra HC = KC => Tam giác HKC cân tại C.

Mà M là trung điểm của HK nên \(CM \bot HK\) (4)

Từ (3) và (4) suy ra C, D, M thẳng hàng.

LG bài 5

Phương pháp giải:

Tính \(f\left( 0 \right),f\left( 1 \right),f\left( { - 1} \right),f\left( {\frac{{ - 1}}{2}} \right)\)

Sử dụng tính chất a, b là số nguyên thì a-b và a+b cũng là số nguyên

Lời giải chi tiết:

+ Ta có: \(f(0) = a{.0^2} + b.0 + c = c\)=> c là số nguyên

+ \(f(1) = a{.1^2} + b.1 + c = a + b + c\) là số nguyên mà c là số nguyên

=> \(a + b\) là số nguyên => 2a + 2b là số nguyên (1)

+ \(f( - 1) = a.{( - 1)^2} + b.( - 1) + c = a - b + c\) là số nguyên mà c là số nguyên

=> \(a - b\) là số nguyên => \(2a - 2b\) là số nguyên (2)

 \(\begin{array}{l}f\left( {\frac{{ - 1}}{2}} \right) = a.{\left( {\frac{{ - 1}}{2}} \right)^2} + b.\left( {\frac{{ - 1}}{2}} \right) + c\\ = \frac{1}{4}a - \frac{1}{2}b + c = \frac{1}{4}.\left( {a - 2b} \right) + c\end{array}\)

Do c là số nguyên nên \(\frac{1}{4}.\left( {a - 2b} \right)\) là số nguyên

=> \(4.\frac{1}{4}.\left( {a - 2b} \right)\) là số nguyên nên \(\left( {a - 2b} \right)\)là số nguyên (3)

Từ (2) và (3) suy ra: \((2a - 2b) - (a - 2b)\) là số nguyên

=> \(2a - 2b - a + 2b\) là số nguyên => a là số nguyên (4)

Từ (1) và (4) suy ra b là số nguyên.

Vậy a, b, c là số nguyên.