Giải đề thi học kì 1 toán lớp 9 năm 2019 - 2020 PGD quận Long Biên

Bài 1  (1,5 điểm). Thực hiện phép tính.

\(a) - 3\sqrt {80}  + 7\sqrt {45}  - \sqrt {500} \)                          \(b)\,\sqrt {{{\left( {\sqrt 3  - 2} \right)}^2}}  + \sqrt {19 + 8\sqrt 3 } \)                        \(c)\,\dfrac{{\sqrt {14} }}{{\sqrt 7 }} - \dfrac{5}{{1 + \sqrt 2 }} + \dfrac{{\sqrt {28}  - 2\sqrt 3 }}{{\sqrt 7  - \sqrt 3 }}\)

Bài 2 (2 điểm). Cho biểu thức  \(P = \left( {\sqrt x  - \dfrac{{x + 2}}{{\sqrt x  + 1}}} \right):\left( {\dfrac{{\sqrt x }}{{\sqrt x  + 1}} + \dfrac{{\sqrt x  - 4}}{{x - 1}}} \right)\)

a) Rút gọn \(P.\)

b) Tính giá trị của \(P\)  với \(x = 4 - 2\sqrt 3 \).

c) Tìm số nguyên \(x\) để biểu thức \(P\) có giá trị nguyên.

Bài 3 (1,5 điểm). Cho hàm số \(y =  - 0,5x\) có đồ thị là \(\left( {{d_1}} \right)\) và hàm số \(y = x + 2\) có đồ thị là \(\left( {{d_2}} \right)\)

a) Vẽ đồ thị \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ \(Oxy.\)

b) Xác định hệ số \(a,b\) của đường thẳng \(\left( d \right):y = ax + b\) biết rằng \(\left( d \right)\) song song với \(\left( {{d_1}} \right)\) và \(\left( d \right)\) cắt \(\left( {{d_2}} \right)\) tại một điểm có tung độ là \( - 3\).

Bài 4 (4,0 điểm).

1) (1 điểm) Cho tam giác \(ABC\) đường cao \(AH\) biết \(BC = 5cm,\) \(AH = 2cm,\) độ lớn góc \(\widehat {ACB} = 30^\circ .\) Tìm độ dài \(AB.\)

2) (3,0 điểm) Cho điểm \(A\) nằm ngoài đường tròn \(\left( O \right),\) kẻ các tiếp tuyến \(AB,\,AC\) với đường tròn \(\left( O \right)\) (\(B\) và \(C\) là 2 tiếp điểm)

a) Chứng minh : Bốn điểm \(A,\,B,\,O,\,C\) cùng thuộc \(1\) đường tròn và \(AO \bot BC.\)

b) Trên cung nhỏ \(BC\) của \(\left( O \right)\) lấy điểm \(M\) bất kì (). Tiếp tuyến tại \(M\) cắt \(AB,\,AC\) lần lượt tại \(D,\,E.\) Chứng minh : Chu vi \(\Delta ADE\) bằng \(2AB.\)

c) Đường thẳng vuông góc với \(AO\) tại \(O\) cắt \(AB\) và \(AC\) lần lượt tại \(P\) và \(Q.\) Chứng minh : \(4PD.QE = P{Q^2}.\)

Bài 5 (1,0 điểm). Cầu Đông Trù bắc qua sông Đuống, nằm trên quốc lộ \(5\) kéo dài, nối xã Đông Hội, huyện Đông Anh ở phía Bắc Hà Nội và phường Ngọc Thụy, quận Long Biên ở phía Nam Hà Nội. Nhịp giữa dài \(120m\) được thiết kế bằng vòm thép nhồi bê tông có hình \(1\) cung tròn. Khoảng cách điểm cao nhất của mái vòm xuống mặt sàn của cầu là \(47m\) (được mô phỏng hình vẽ dưới). Hãy tính độ dài bán kính \(R\) của đường tròn chứa cung tròn là nhịp giữa của cầu Đông Trù ? (kết quả làm tròn đến \(2\) chữ số thập phân).

 

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn

 

Bài 1 (VD):

Phương pháp:

a) Đưa thừa số ra ngoài dấu căn, sử dụng \(\sqrt {{A^2}B}  = \left| A \right|\sqrt B \).

b) Đưa thừa số ra ngoài dấu căn, sử dụng \(\sqrt {{A^2}B}  = \left| A \right|\sqrt B \).

c) Thực hiện rút gọn bằng cách đưa tử và mẫu về dạng tích kết hợp trục căn thức ở mẫu: \(\dfrac{C}{{\sqrt A  + \sqrt B }} = \dfrac{{C\left( {\sqrt A  - \sqrt B } \right)}}{{A - B}}\)

Cách giải:

a) \( - 3\sqrt {80}  + 7\sqrt {45}  - \sqrt {500} \)

\(\begin{array}{l} =  - 3\sqrt {16.5}  + 7.\sqrt {9.5}  - \sqrt {100.5} \\ =  - 12\sqrt 5  + 21\sqrt 5  - 10\sqrt 5 \\ =  - \sqrt 5 \end{array}\)

b) \(\sqrt {{{\left( {\sqrt 3  - 2} \right)}^2}}  + \sqrt {19 + 8\sqrt 3 } \)

\(\begin{array}{l} = \left| {\sqrt 3  - 2} \right| + \sqrt {{{\left( {4 + \sqrt 3 } \right)}^2}} \\ = 2 - \sqrt 3  + 4 + \sqrt 3 \\ = 6\end{array}\)

c) \(\dfrac{{\sqrt {14} }}{{\sqrt 7 }} - \dfrac{5}{{1 + \sqrt 2 }} + \dfrac{{\sqrt {28}  - 2\sqrt 3 }}{{\sqrt 7  - \sqrt 3 }}\)

\(\begin{array}{l} = \sqrt 2  - \dfrac{{5\left( {1 - \sqrt 2 } \right)}}{{1 - 2}} + \dfrac{{2\left( {\sqrt 7  - \sqrt 3 } \right)}}{{\sqrt 7  - \sqrt 3 }}\\ = \sqrt 2  + 5\left( {1 - \sqrt 2 } \right) + 2\\ = \sqrt 2  + 5 - 5\sqrt 2  + 2\\ = 7 - 4\sqrt 2 \end{array}\)

Bài 2 (VD):

Phương pháp:

a) Qui đồng, khử mẫu và rút gọn.

b) Rút gọn \(x\) rồi thay vào biểu thức đã rút gọn được ở câu a.

c) Biến đổi \(P\) và sử dụng tính chất của ước bội để suy ra điều kiện \(P \in \mathbb{Z}\).

Cách giải:

a) Rút gọn \(P.\)

\(P = \left( {\sqrt x  - \dfrac{{x + 2}}{{\sqrt x  + 1}}} \right):\left( {\dfrac{{\sqrt x }}{{\sqrt x  + 1}} + \dfrac{{\sqrt x  - 4}}{{x - 1}}} \right)\)

\( = \left( {\dfrac{{\sqrt x \left( {\sqrt x  + 1} \right) - \left( {x + 2} \right)}}{{\sqrt x  + 1}}} \right)\) \(:\left( {\dfrac{{\sqrt x \left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}} + \dfrac{{\sqrt x  - 4}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}} \right)\)

\( = \dfrac{{x + \sqrt x  - x - 2}}{{\sqrt x  + 1}}:\dfrac{{x - \sqrt x  + \sqrt x  - 4}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}\)

\(\begin{array}{l} = \dfrac{{\sqrt x  - 2}}{{\sqrt x  + 1}}:\dfrac{{x - 4}}{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}\\ = \dfrac{{\sqrt x  - 2}}{{\sqrt x  + 1}}.\dfrac{{\left( {\sqrt x  + 1} \right)\left( {\sqrt x  - 1} \right)}}{{\left( {\sqrt x  + 2} \right)\left( {\sqrt x  - 2} \right)}}\\ = \dfrac{{\sqrt x  - 1}}{{\sqrt x  + 2}}\end{array}\)

ĐKXĐ: \(\left\{ \begin{array}{l}x \ge 0\\x - 1 \ne 0\\x - 4 \ne 0\end{array} \right. \Leftrightarrow \left\{ \begin{array}{l}x \ge 0\\x \ne 1\\x \ne 4\end{array} \right.\)

b) Tính giá trị của \(P\)  với \(x = 4 - 2\sqrt 3 \).

Ta có: \(x = 4 - 2\sqrt 3  = {\left( {\sqrt 3  - 1} \right)^2}\)\( \Rightarrow \sqrt x  = \sqrt 3  - 1\) (TMĐKXĐ)

Thay vào \(P\) ta có: \(P = \dfrac{{\sqrt 3  - 1 - 1}}{{\sqrt 3  - 1 + 2}} = \dfrac{{\sqrt 3  - 2}}{{\sqrt 3  + 1}}\) \( = \dfrac{{\left( {\sqrt 3  - 2} \right)\left( {\sqrt 3  - 1} \right)}}{{3 - 1}} = \dfrac{{5 - 3\sqrt 3 }}{2}\)

Vậy với \(x = 4 - 2\sqrt 3 \) thì \(P = \dfrac{{5 - 3\sqrt 3 }}{2}\)

c) Tìm số nguyên \(x\) để biểu thức \(P\) có giá trị nguyên.

Ta có: \(P = \dfrac{{\sqrt x  - 1}}{{\sqrt x  + 2}} = \dfrac{{\sqrt x  + 2 - 3}}{{\sqrt x  + 2}}\) \( = 1 - \dfrac{3}{{\sqrt x  + 2}}\)

Vì \(x \in \mathbb{Z},1 \in \mathbb{Z}\) nên để \(P \in \mathbb{Z}\) thì \(\sqrt x  + 2 \in U\left( 3 \right) = \left\{ { \pm 1; \pm 3} \right\}\)

Bảng giá trị:

 

Vậy không có giá trị \(x\) nguyên thỏa mãn điều kiện xác định để biểu thức \(P\) có giá trị nguyên.

Bài 3 (VD ):

Phương pháp:

a) Lập bảng giá trị các điểm đi qua của mỗi đồ thị hàm số và vẽ đồ thị.

b) Sử dụng \(d//d'\) thì \(a = a',b \ne b'\).

Cách giải:

a) Vẽ đồ thị \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ \(Oxy.\)

Vẽ \(\left( {{d_1}} \right)\) và \(\left( {{d_2}} \right)\) trên cùng một mặt phẳng tọa độ \(Oxy\)

Bảng giá trị \(y =  - 0,5x\)

Bảng giá trị \(y = x + 2\)

Đồ thị:

 

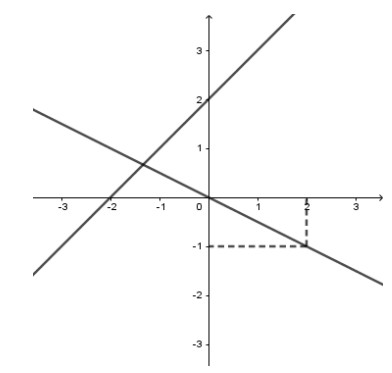
b) Xác định hệ số \(a,b\) của đường thẳng \(\left( d \right):y = ax + b\) biết rằng \(\left( d \right)\) song song với \(\left( {{d_1}} \right)\) và \(\left( d \right)\) cắt \(\left( {{d_2}} \right)\) tại một điểm có tung độ là \( - 3\).

Vì \(\left( d \right)//\left( {{d_1}} \right)\) nên \(a =  - 0,5\) và \(b \ne 0.\) Khi đó \(\left( d \right):y =  - 0,5x + b\)

Gọi \(A\left( {{x_0}; - 3} \right)\) là tọa độ giao điểm của \(\left( d \right)\) và \(\left( {{d_2}} \right)\)

+\(A\left( {{x_0}; - 3} \right) \in \left( {{d_2}} \right)\) \( \Rightarrow  - 3 = {x_0} + 2 \Rightarrow {x_0} =  - 5\)

+\(A\left( { - 5; - 3} \right) \in \left( d \right)\) \( \Rightarrow  - 3 =  - 0,5.\left( { - 5} \right) + b\) \( \Rightarrow b =  - 5,5\) (TMĐK)

Vậy \(\left( d \right):y =  - 0,5x - 5,5\)

Bài 4 (VD ):

Phương pháp:

1) Sử dụng giá trị lượng giác của một góc nhọn trong tam giác vuông tính \(HC\).

Từ đó tính \(HB\) và suy ra \(AB\) theo định lí Pi-ta-go.

2) a) +) Gọi \(N\) là trung điểm \(AO\) và chứng minh \(NO = NA = NB = NC\)

+) Chứng minh \(AO\) là trung trực của đoạn \(BC.\)

b) Sử dụng tính chất tiếp tuyến cắt nhau.

c) Chứng minh các tam giác \(\Delta ODE \sim \Delta QOE\) và \( \Rightarrow \Delta ODE \sim \Delta PDO\) suy ra các tỉ số đồng dạng.

Cách giải:

1) (1 điểm) Cho tam giác \(ABC\) đường cao \(AH\) biết \(BC = 5cm,\) \(AH = 2cm,\) độ lớn góc \(\widehat {ACB} = 30^\circ .\) Tìm độ dài \(AB.\)

 

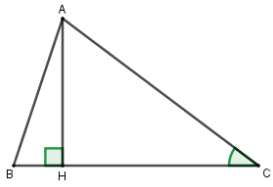
Tam giác \(AHC\) vuông tại \(H\) có:

\(HC = \dfrac{{AH}}{{\tan C}} = \dfrac{2}{{\tan {{30}^0}}} = 2\sqrt 3 cm;\) \(BH = BC - CH = 5 - 2\sqrt 3 cm\)

Tam giác \(AHB\) vuông tại \(H\) có \(A{B^2} = A{H^2} + H{B^2}\)

\( \Rightarrow AB = \sqrt {A{H^2} + B{H^2}} \)  \( = \sqrt {{2^2} + {{\left( {5 - 2\sqrt 3 } \right)}^2}} \) \( = 41 - 20\sqrt 3  \approx 2,52cm\)

Vậy \(AB = 2,52\left( {cm} \right)\).

2) (3,0 điểm) Cho điểm \(A\) nằm ngoài đường tròn \(\left( O \right),\) kẻ các tiếp tuyến \(AB,\,AC\) với đường tròn \(\left( O \right)\) (\(B\) và \(C\) là 2 tiếp điểm)

 

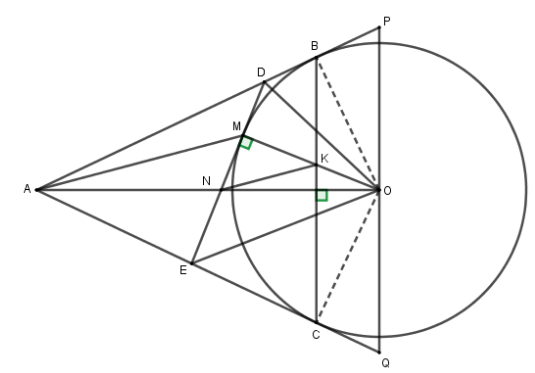
a) Chứng minh : Bốn điểm \(A,\,B,\,O,\,C\) cùng thuộc \(1\) đường tròn và \(AO \bot BC.\)

Gọi \(N\) là trung điểm của \(AO\).

Tam giác \(AOB\) vuông tại \(B\) nên \(BN = \dfrac{1}{2}AO = NA = NO\) (1)

Tương tự ta có \(CN = \dfrac{1}{2}AO = NA = NO\) (2)

Từ (1) và (2) suy ra \(NB = NA = NO = NC\).

Vậy \(A,B,O,C\) cùng thuộc đường tròn tâm \(N,\) đường kính \(AO\).

Vì \(AB,AC\) là các tiếp tuyến nên \(AB = AC\left( {t/c} \right)\).

Mà \(OA = OB\) (bán kính) nên \(AO\) là trung trực của đoạn \(BC.\)

Suy ra \(AO\) vuông góc \(BC\)

b) Trên cung nhỏ \(BC\) của \(\left( O \right)\) lấy điểm \(M\) bất kì (). Tiếp tuyến tại \(M\) cắt \(AB,\,AC\) lần lượt tại \(D,\,E.\) Chứng minh : Chu vi \(\Delta ADE\) bằng \(2AB.\)

Chu vi \(\Delta ADE = AD + DE + AE\)

Mà : \(DM = DB\) (tiếp tuyến \(MD\) và \(DB\) cắt nhau tại \(D\))

\(ME = CE\) (tiếp tuyến \(ME\) và \(CE\) cắt nhau tại \(E\))

Suy ra chu vi \(\Delta ADE\) là:

\(AD + DB + AE + EC\) \( = AB + AC = 2AB\)

c) Đường thẳng vuông góc với \(AO\) tại \(O\) cắt \(AB\) và \(AC\) lần lượt tại \(P\) và \(Q.\) Chứng minh : \(4PD.QE = P{Q^2}.\)

Theo tính chất của hai tiếp tuyến của đường tròn, ta có :

\(\widehat {DOM} = \dfrac{1}{2}\widehat {BOM},\,\widehat {MOE} = \dfrac{1}{2}\widehat {MOC}\)

Cộng vế theo vế, ta được :

\(\widehat {DOE} = \dfrac{1}{2}\widehat {BOC}\)

Mà \(\dfrac{1}{2}\widehat {BOC} = \widehat {AOC} = \widehat {OQE}\) (vì \(\widehat {AOC}\) và \(\widehat {OQE}\) cùng phụ với \(\widehat {QAO}\))

Nên \(\widehat {DOE} = \widehat {OQE}\)

Xét tam giác \(ODE\) và tam giác \(QOE,\) ta có :

\(\widehat {DOE} = \widehat {QOE}\,\,\left( {cmt} \right)\)

\(\widehat {OED} = \widehat {OEQ}\) (tính chất hai tiếp tuyến cắt nhau)

\( \Rightarrow \Delta ODE \sim \Delta QOE\left( {g.g} \right)\)

Chứng minh tương tự \( \Rightarrow \Delta ODE \sim \Delta PDO\)

\( \Rightarrow \Delta QOE \sim \Delta PDO\) (tính chất bắc cầu)

\( \Rightarrow \dfrac{{QO}}{{PD}} = \dfrac{{QE}}{{PO}}\) \( \Rightarrow PD.QE = PO.QO\) \( = \dfrac{{PQ}}{2} \cdot \dfrac{{PQ}}{2} = \dfrac{{P{Q^2}}}{4}\)

\( \Rightarrow 4PD.QE = P{Q^2}\). (đpcm)

Bài 5 (VD ):

Phương pháp:

Đặt bán kính bằng \(R\), áp dụng định lí Pi-ta-go trong tam giác vuông tìm \(R\).

Cách giải:

 

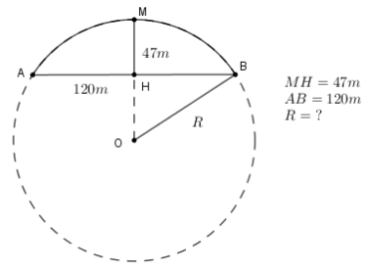
Vì \(OH \bot AB\) tại \(H\) nên \(H\) là trung điểm của \(AB,\) do đó \(HA = HB = 60\left( m \right)\)

Kéo dài \(OH\) cắt đường tròn tại \(M\), khi đó \(OM = R\) và là khoảng cách lớn nhất nên \(M\) là điểm cao nhất của mái vòm hay \(HM = 47m\).

\( \Rightarrow \)\(HO = OM - HM = R - 47\left( m \right)\)

Áp dụng định lý Pitago vào tam giác vuông \(OHB\) ta có:

\(O{B^2} = O{H^2} + H{B^2}\) \( \Rightarrow {60^2} + {\left( {R - 47} \right)^2} = {R^2}\)

\( \Leftrightarrow 3600 + {R^2} - 94R + 2209 = {R^2}\) \( \Leftrightarrow  - 94R =  - 5809\) \( \Leftrightarrow R = \dfrac{{5809}}{{94}} \approx 62,00\left( m \right)\)

Vậy độ dài bán kính \(R\) của đường tròn chứa cung tròn là nhịp giữa của cầu Đông Trù là \(62\) mét.