Giải đề thi học kì 1 toán lớp 10 năm 2020-2021 trường THPT Đống Đa

Đề bài

Câu 1( 3,5 điểm) Cho hàm số :\(y = {x^2} - 2mx + 3\)

1. Khảo sát sự biến thiên và vẽ đồ thị (P) của hàm số khi \(m = 2\).

2. Dựa vào đồ thị (P), biện luận theo k số nghiệm của phương trình:\({x^2} - 4x + k = 0\)

3. Tìm giá trị của \(m\) để hàm số nghịch biến trên khoảng \(\left( { - \infty ;2020} \right)\).

Câu 2(2,5 điểm) Giải các phương trình sau:

1. \({x^2} - 2x - 5\left| {x - 1} \right| - 5 = 0\)

2. \(\sqrt {{x^2} - 3x + 3}  - 2x + 3 = 0\)

Câu 3(1 điểm) Cho phương trình:

\({x^4} - 4{x^2} + a = 0\)( với a là tham số )

1. Giải phương trình đã cho khi \(a =  - 5\)

2. Xác định a để phương trình đã cho có bốn nghiệm phân biệt thuộc đoạn \(\left[ { - 2;3} \right]\)

Câu 4(3 điểm)

Trong hộ trục tọa độ (Oxy) cho bốn điểm:\(A\left( {2; - 1} \right),B\left( {3;4} \right),C\left( {4;3} \right),D\left( {3; - 2} \right)\)

1. Chứng minh bốn điểm đã cho tạo thành hình bình hành \(ABCD\). Tìm tọa độ tâm hình bình hành đó.

2. Gọi G là trọng tâm tam giác ABC. Tìm tọa độ điểm E thỏa mãn: \(\overrightarrow {BE}  = 2\overrightarrow {AD}  - 3\overrightarrow {GC} \).

3. Lấy điểm M di động. Dựng điểm N sao cho \(\overrightarrow {MN}  = \overrightarrow {MA}  + 3\overrightarrow {MB}  - 2\overrightarrow {MC} \). Chứng minh rằng MN luôn đi qua một điểm cố định.

Lời giải chi tiết

Câu 1(VD)

Phương pháp:

1.

Thay \(m = 2\) vào hàm số.

Tìm khoảng đồng biến, nghịch biến của hàm số.

Đồ thị: Xác định bề lõm, đỉnh và trục đối xứng của đồ thị và một số điểm thuộc đồ thị.

2.

Đặt hàm số của (P): \(y = f\left( x \right)\).

Đưa phương trình đã cho về dạng\(f\left( x \right) = g\left( x \right)\)

Số nghiệm của phương trình \(f\left( x \right) = g\left( x \right)\) là số giao điểm của hai đồ thị \(y = f\left( x \right)\) và \(y = g\left( x \right)\).

3. Tìm khoảng nghịch biến D của hàm số \(y = {x^2} - 2mx + 3\). Hàm số nghịch biến trên \(\left( { - \infty ;2020} \right)\) khi và chỉ khi \(\left( { - \infty ;2020} \right) \subset D\).

Giải:

1.

Thay \(m = 2\) vào hàm số ta  được (P):\(y = {x^2} - 4x + 3\).

Do \(1 > 0\), hàm số đồng biến trên \(\left( {2; + \infty } \right)\), nghịch biến trên \(\left( { - \infty ;2} \right)\).

Bảng biến thiên:

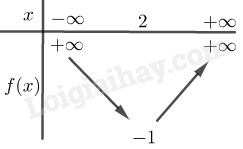
Đồ thị:

Đồ thị có bề lõm hướng lên trên, đồ thị có đỉnh \(\left( {2; - 1} \right)\). Đồ thị nhận đường thẳng \(x = 2\) làm trục đối xứng.

Đồ thị đi qua điểm \(A\left( {0;3} \right),B\left( {1;0} \right),C\left( {3;0} \right)\).

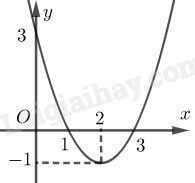
2. Đặt \(f\left( x \right) = {x^2} - 4x + 3\)

\(\begin{array}{l}{x^2} - 4x + k = 0\left( 1 \right)\\ \Leftrightarrow {x^2} - 4x + 3 = 3 - k\end{array}\)

Số nghiệm của (1) bằng số giao điểm của \((P):y = f\left( x \right)\) và \(\left( d \right):y = 3 - k\).

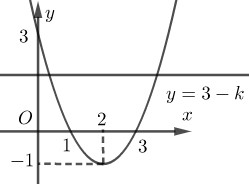
Từ đồ thị ta thấy:

Số giao điểm bằng 0 khi và chỉ khi \(3 - k <  - 1 \Leftrightarrow k > 4\).

Số giao điểm bằng 1 khi và chỉ khi \(3 - k =  - 1 \Leftrightarrow k = 4\).

Số giao điểm bằng 2 khi và chỉ khi \(3 - k >  - 1 \Leftrightarrow k < 4\).

3.

Hàm số nghịch biến trên \(\left( { - \infty ;m} \right)\). Hàm số đã cho nghịch biến trên \(\left( { - \infty ;2020} \right)\) khi và chỉ khi \(\left( { - \infty ;2020} \right) \subset \left( { - \infty ;m} \right) \Leftrightarrow m \ge 2020\).

Câu 2(VD):

Phương pháp:

1. Đặt \(\left| {x - 1} \right| = t\left( {t \ge 0} \right)\), đưa phương trình về phương trình ẩn t.

2. \(\sqrt A  = B \Leftrightarrow \left\{ \begin{array}{l}B \ge 0\\A = {B^2}\end{array} \right.\)

Giải:

1.

\({x^2} - 2x - 5\left| {x - 1} \right| - 5 = 0\)

\( \Leftrightarrow {\left( {x - 1} \right)^2} - 5\left| {x - 1} \right| - 6 = 0\)(1).

Đặt \(\left| {x - 1} \right| = t\left( {t \ge 0} \right)\). Phương trình (1) trở thành:

 \({t^2} - 5t - 6 = 0 \Leftrightarrow t = 6\)

\(\begin{array}{l} \Leftrightarrow \left| {x - 1} \right| = 6 \Leftrightarrow \left[ \begin{array}{l}x - 1 = 6\\x - 1 =  - 6\end{array} \right.\\ \Leftrightarrow \left[ \begin{array}{l}x = 7\\x =  - 5\end{array} \right.\end{array}\)

2. \(\sqrt {{x^2} - 3x + 3}  - 2x + 3 = 0\)

\(\begin{array}{l}\sqrt {{x^2} - 3x + 3}  = 2x - 3\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge \dfrac{3}{2}\\3{x^2} - 9x + 6 = 0\end{array} \right.\\ \Leftrightarrow \left\{ \begin{array}{l}x \ge \dfrac{3}{2}\\\left[ \begin{array}{l}x = 1\\x = 2\end{array} \right.\end{array} \right. \Leftrightarrow x = 2\end{array}\)

Câu 3(VD)

Phương pháp:

1. Thay \(a =  - 5\) vào phương trình. Đặt \({x^2} = t\left( {t \ge 0} \right)\), đưa về phương trình ẩn t. Giải t tìm x.

2. Đưa về hai phương trình bậc hai

\(\begin{array}{l}{x^4} - 4{x^2} + a = 0\left( * \right)\\ \Leftrightarrow {\left( {{x^2} - 2} \right)^2} = 4 - a\\ \Leftrightarrow \left\{ \begin{array}{l}a < 4\\\left[ \begin{array}{l}{x^2} = 2 + \sqrt {4 - a} (1)\\{x^2} = 2 - \sqrt {4 - a} \left( 2 \right)\end{array} \right.\end{array} \right.\end{array}\)

(*) có 4 nghiệm phân biệt khi và chỉ khi (1) có 2 nghiệm phân biệt và (2) có 2 nghiệm phân biệt không trùng với phương trình (1).

Giải:

1. Thay \(a =  - 5\) vào phương trình ta được \({x^4} - 4{x^2} - 5 = 0\)(1)

Đặt \({x^2} = t\left( {t \ge 0} \right)\), (1) trở thành:

\(\begin{array}{l}{t^2} - 4t - 5 = 0 \Leftrightarrow \left[ \begin{array}{l}t =  - 1\\t = 5\end{array} \right.\\ \Leftrightarrow t = 5 \Leftrightarrow {x^2} = 5\end{array}\)

\(x =  \pm \sqrt 5 \)

2.

\(\begin{array}{l}{x^4} - 4{x^2} + a = 0\left( * \right)\\ \Leftrightarrow {\left( {{x^2} - 2} \right)^2} = 4 - a\\ \Leftrightarrow \left\{ \begin{array}{l}a < 4\\\left[ \begin{array}{l}{x^2} = 2 + \sqrt {4 - a} (1)\\{x^2} = 2 - \sqrt {4 - a} \left( 2 \right)\end{array} \right.\end{array} \right.\end{array}\)

(*) có 4 nghiệm phân biệt khi và chỉ khi (1) có 2 nghiệm phân biệt và (2) có 2 nghiệm phân biệt không trùng với phương trình (1)

(2) có 2 nghiệm phân biệt \( \Leftrightarrow 2 - \sqrt {4 - a}  > 0 \Leftrightarrow a > 0\)

Khi \(0 < a < 4\) các nghiệm của (*) đều thỏa mãn \({x^2} < 4\). Hay (*) luôn có có 4 nghiệm phân biệt thuộc đoạn \(\left[ { - 2;2} \right]\)

Vậy \(0 < a < 4\) thì phương trình đã cho có bốn nghiệm phân biệt thuộc đoạn \(\left[ { - 2;3} \right]\)

Câu 4(VD)

Phương pháp:

1. \(ABCD\) là hình bình hành \( \Leftrightarrow \overrightarrow {AB}  = \overrightarrow {DC} \)

Tâm O của hình bình hành: \(\left\{ \begin{array}{l}{x_O} = \dfrac{{{x_A} + {x_C}}}{2}\\{y_O} = \dfrac{{{y_A} + {y_C}}}{2}\end{array} \right.\)

2. Tìm điểm G.

Sử dụng công thức: \(\overrightarrow {AD}  = \overrightarrow {BD}  - \overrightarrow {BA} \), tính chất trọng tâm \(\overrightarrow {BG}  = \dfrac{2}{3}\overrightarrow {BO} \), tính chất trung điểm \(\overrightarrow {BO}  = \dfrac{1}{2}\overrightarrow {BD} \).

3. Gọi \(I\) là trung điểm của \(MN\).

Sử dụng quy tắc cộng, trừ vectơ chứng minh \(I\) là điểm cố định.

Cách giải:

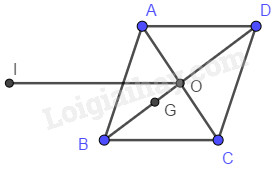
1.

Ta có \(\overrightarrow {AB}  = \left( {3 - 2;4 - \left( { - 1} \right)} \right) = \left( {1;5} \right)\);\(\overrightarrow {DC}  = \left( {4 - 3;3 - \left( { - 2} \right)} \right) = \left( {1;5} \right)\)

\( \Rightarrow \overrightarrow {AB}  = \overrightarrow {DC} \)\( \Rightarrow ABCD\) là hình bình hành.

Tâm O của hình bình hành là chung điểm chung của AC và BD nên : \(\left\{ \begin{array}{l}{x_O} = \dfrac{{{x_A} + {x_C}}}{2} = 3\\{y_O} = \dfrac{{{y_A} + {y_C}}}{2} = 1\end{array} \right. \Rightarrow O\left( {3;1} \right)\)

2.

\(\begin{array}{l}\overrightarrow {BE}  = 2\overrightarrow {AD}  - 3\overrightarrow {GC} \\ = 2\left( {\overrightarrow {BD}  - \overrightarrow {BA} } \right) - 3\left( {\overrightarrow {BC}  - \overrightarrow {BG} } \right)\\ = 2\overrightarrow {BD}  - 2\overrightarrow {BA}  - 3\overrightarrow {BC}  + 3\overrightarrow {BG} \\ = 2\overrightarrow {BD}  - 2\overrightarrow {BD}  - \overrightarrow {BC}  + 3.\dfrac{2}{3}\overrightarrow {BO} \\\left. \begin{array}{l} = \overrightarrow {CB}  + \overrightarrow {BD}  = \overrightarrow {CD} \\\overrightarrow {CD}  = \overrightarrow {BA} \end{array} \right\} \Rightarrow E \equiv A\end{array}\)

3.

\(\begin{array}{l}\overrightarrow {MN}  = \overrightarrow {MA}  + 3\overrightarrow {MB}  - 2\overrightarrow {MC} \\ = \overrightarrow {MA}  + \overrightarrow {MC}  + 3\overrightarrow {CB}  = 2\overrightarrow {MO}  + 3\overrightarrow {CB} \\ \Leftrightarrow \overrightarrow {MN}  - \overrightarrow {MO}  - \overrightarrow {MO}  = 3\overrightarrow {CB} \\ \Leftrightarrow \overrightarrow {ON}  + \overrightarrow {OM}  = 3\overrightarrow {CB} \\ \Leftrightarrow 2\overrightarrow {OI}  = 3\overrightarrow {CB}  \Leftrightarrow \overrightarrow {OI}  = \dfrac{3}{2}\overrightarrow {CB} \end{array}\)

Do O,C,B là các điểm cố định nên I là điểm cố định.

Vậy MN luôn đi qua điểm cố định I.