Giải đề thi học kì 1 lý lớp 10 năm 2020 - 2021 trường THPT Nguyễn Huệ

Đề bài

Câu I: (2 điểm)

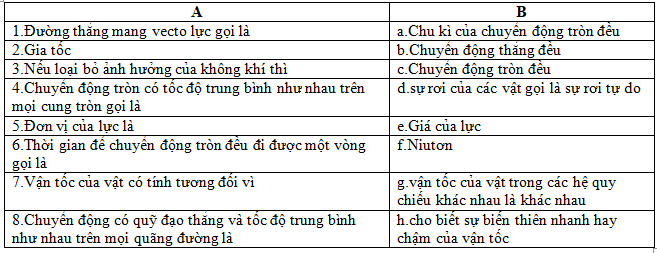
Ghép các nội dung ở cột A với cột B để viết lại thành câu đúng.

Câu II: (2 điểm)

Phát biểu nội dung định luật I Niutơn. Quán tính là gì? Lấy ví dụ về một vật có quán tính?

Câu III: (2 điểm)

Một vật thả rơi tự do tại nơi có \(g = 10m/{s^2}\). Thời gian từ lúc thả đến lúc chạm đất là 2s. Hãy tính:

1) Độ cao lúc thả vật.

2) Vận tốc của vật lúc chạm đất

Câu IV: (1 điểm)

Lò xo có chiều dài tự nhiên 24 cm, độ cứng k = 25 N/m treo thẳng đứng tại nơi có \(g = 10m/{s^2}\). Vật treo có khối lượng 0,2 kg. Tính độ biến dạng của lò xo khi vật treo ở vị trí cân bằng và chiều dài của lò xo khi đó?

Câu V: (3 điểm)

Vật m = 2kg (ban đầu đứng yên) được kéo trượt trên mặt phẳng nằm ngang dưới tác dụng của lực kéo theo phương ngang có độ lớn 6 N. Hệ số ma sát là 0,25, lấy \(g = 10m/{s^2}\). Hãy tính:

1) Gia tốc của chuyển động

2) Ngay sau khi vật trượt được quãng đường s thì ngừng tác dụng lực kéo. Biết rằng vật chỉ đi thêm được quãng đường 11,25 m nữa thì dừng lại. Tìm s?

Lời giải chi tiết

HƯỚNG DẪN GIẢI CHI TIẾT

Thực hiện: Ban chuyên môn

Câu I:

Phương pháp

Vận dụng lý thuyết chương 1.

Cách giải

1 – e                2 – h                3 – d                4 – b

5 – f                 6 – a                7 – g                8 - b

Câu II:

Phương pháp

Vận dụng lý thuyết bài “Ba định luật Niutơn”.

Cách giải

- Nội dung định luật I Niutơn: Nếu không chịu tác dụng của lực nào hoặc chịu tác dụng của các lực có hợp lực bằng không, thì vật đang đứng yên sẽ tiếp tục đứng yên, đang chuyển động sẽ tiếp tục chuyển động thẳng đều.

- Quán tính là tính chất của mọi vật có xu hướng bảo toàn vận tốc cả về hướng và độ lớn.

Ví dụ: Khi xe phanh gấp thì người ngồi trên xe vẫn theo quán tính mà chuyển động về phía trước.

Câu III:

Phương pháp

Sử dụng các công thức: \(\left\{ \begin{array}{l}h = \frac{1}{2}g{t^2}\\v = \sqrt {2gh} \end{array} \right.\)

Cách giải

1)

Độ cao lúc thả vật là:

\(h = \frac{1}{2}g{t^2} = \frac{1}{2}{.10.2^2} = 20m\)

2)

Vận tốc của vật lúc chạm đất là:

\(v = \sqrt {2gh}  = \sqrt {2.10.20}  = 20m/s\)

Vậy \(\left\{ \begin{array}{l}h = 20m\\v = 20m/s\end{array} \right.\)

Câu IV:

Phương pháp

Áp dụng định luật Húc.

Cách giải

Khi vật ở vị trí cân bằng thì trọng lực P cân bằng với lực đàn hồi => \({F_{dh}} = P\)

Khi đó, ta có:

 \(\begin{array}{l}{F_{dh}} = P \Leftrightarrow k\left| {\Delta l} \right| = mg\\ \Leftrightarrow 25\left| {\Delta l} \right| = 0,2.10\\ \Leftrightarrow \Delta l = \frac{{0,2.10}}{{25}} = 0,08m = 8cm\end{array}\)

Ta có:

\(\Delta l = l - {l_0} \Leftrightarrow l = {l_0} + \Delta l = 24 + 8 = 30cm\)

Vậy độ biến dạng của lò xo là \(\Delta l = 8cm\); chiều dài của lò xo ở vị trí cân bằng là l = 30cm.

Câu IV:

Phương pháp

- Áp dụng định luật II Niutơn.

- Vận dụng các công thức của chuyển động thẳng biến đổi đều.

Cách giải

1)

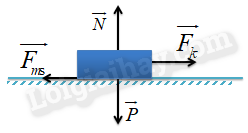
Các lực tác dụng lên vật gồm: \(\overrightarrow P ,\overrightarrow N ,\overrightarrow {{F_{m{\rm{s}}}}} ,\overrightarrow {{F_k}} \) có phương và chiều như hình vẽ.

Chọn chiều dương cùng chiều chuyển động.

Phương trình định luật II Niuton viết cho vật là:

\(\overrightarrow P  + \overrightarrow N  + \overrightarrow {{F_{m{\rm{s}}}}}  + \overrightarrow {{F_k}}  = m\overrightarrow a \) (*)

Chiếu phương trình (*) lên chiều dương ta được:

\({F_k} - {F_{m{\rm{s}}}} = ma\)

\(\begin{array}{l} \Leftrightarrow {F_k} - \mu mg = ma\\ \Leftrightarrow a = \frac{{{F_k} - \mu mg}}{m}\\ \Leftrightarrow a = \frac{{6 - 0,25.2.10}}{2} = 0,5m/{s^2}\end{array}\)

2)

Vận tốc của vật sau 10s là:

\(v = {v_0} + at = 0 + 0,5.10 = 5\left( {m/s} \right)\)

Quãng đường vật trượt được sau 10s là:

\(s = {v_0}t + \frac{1}{2}a{t^2} = 0.10 + \frac{1}{2}.0,{5.10^2} = 25m\)

3)

Khi ngừng tác dụng lực kéo, ta có:

\(\begin{array}{l}0 - {F_{m{\rm{s}}}} = ma'\\ \Leftrightarrow a' =  - \frac{{{F_{m{\rm{s}}}}}}{m} =  - \frac{{0,25.2.10}}{2} =  - 2,5m/{s^2}\end{array}\)

Vận tốc của vật trước khi ngừng tác dụng lực kéo là:

\(\begin{array}{l}v_2^2 - v_1^2 = 2{\rm{a}}'s'\\ \Leftrightarrow  - v_1^2 = 2.( - 2,5).11,25\\ \Leftrightarrow {v_1} = 7,5m/s\end{array}\)

Thời gian vật trượt được được quãng đường s là:

\({v_1} = {v_0} + at \Rightarrow t = \frac{{{v_1}}}{a} = \frac{{7,5}}{{0,5}} = 15{\rm{s}}\)

Vậy quãng đường s là:

\(s = {v_0}t + \frac{1}{2}a{t^2} = 0.15 + \frac{1}{2}.0,{5.15^2} = 56,25m\)